ALTRI METODI INFERENZIALI:

NORMAL SCORES E RICAMPIONAMENTO

 

 

22.1.  I NORMAL SCORES DI VAN DER WAERDEN; CENNI SU RANDOM NORMAL DEVIATES E SU EXPECTED NORMAL SCORES.

 

 

Per test sulla tendenza centrale di uno, di due e di k campioni sia dipendenti che indipendenti e per la regressione e la correlazione, negli anni 1952-53 B. L. van der Waerden nei due articoli dal titolo Order tests for the two-sample problem and their power, pubblicati sulla rivista olandese Proceedings Koninklijke Nederlandse Akademie van Wetenschappen, A

-  il primo su 55 Indagationes Mathematicae vol. 14, pp. 453-458

-  il secondo su 56 Indagationes Mathematicae vol. 15, pp. 303-316, con correzioni riportate nel vol. 56, p. 80)

ha sviluppato un’idea semplice, che permette di normalizzare la distribuzione di dati, qualunque sia la sua forma originaria. Il metodo, con applicazioni a vari casi, è riportato in numerosi testi internazionali di statistica applicata. Tra quelli di edizione recente, possono essere citati

-  P. Sprent and N. C. Smeeton, 2001, Applied Nonparametric Statistical Methods (3^rd ed. Chapman & Hall/CRC, London, 982 p.),

-  David J. Sheskin, 2000, Handbook of Parametric and Nonparametric Statistical Procedures (2^nd ed. Chapman & Hall/CRC, London, 982 p.),

-  W. J. Conover, 1999, Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.).

 

Il metodo, detto dei Normal Scores, è utilmente applicato sia nel caso di misure a intervalli e/o di rapporti quando la distribuzione si allontana dalla normalità, sia nel caso di punteggi di tipo ordinale. La procedura è lunga, quando effettuata manualmente e con un numero elevato di dati. Ma è facile da comprendere e soprattutto da applicare con i computer. Quindi, seppure proposta poco dopo il 1950, si sta affermando ora nella ricerca applicata, in sostituzione o complemento delle analisi condotte mediante i metodi classici di statistica non parametrica, già presentati nei capitoli precedenti. Tuttavia molti programmi informatici, anche tra quelli a grande diffusione internazionale, ignorano questa metodologia.

 

La logica è semplice:

1 - dopo aver trasformato la serie di misure o punteggi in ranghi, quindi disponendo di N ranghi,

 

2 - si trasforma ogni rango (k) nel quantile corrispondente,

 mediante la relazione

 dove

 k = rango del valore osservato (1,  2,  3,  … N)

 N = numero totale di misure e rango maggiore;

 

 3 – infine, i quantili sono trasformati in deviazioni standard (in valori z, da cui normal-scores), utilizzando la distribuzione normale cumulata.

 

In questa triplice serie di passaggi, la forma della distribuzione delle misure raccolte è modificata due volte: dalla distribution free alla rettangolare come sono i ranghi e da questa alla normale come sono i valori z costruita sui quantili corrispondenti. In modo più specifico, 

-  dalla distribuzione originale che può avere una forma qualsiasi, ma di norma è lontana dalla normalità (altrimenti tutta la procedura diverrebbe inutile e sarebbe sufficiente utilizzare direttamente un test parametrico),

 -  mediante la prima trasformazione dei valori in ranghi si determina una distribuzione rettangolare,

-  mantenuta nella successiva trasformazione dei ranghi in quantili;

-  infine, con la trasformazione di questi quantili in valori (Z) di deviata normale standardizzata (normal scores), si ottiene una distribuzione normale.

 

In queste variazioni della forma della distribuzione, è modificata anche la potenza del test. Se le misure originali erano su una scala ad intervalli o di rapporti, nelle quali la distanza tra i valori è una indicazione importante da permettere il calcolo della media e della varianza, in questa serie di passaggi e in particolare nella prima trasformazione in ranghi si ha una perdita di informazione. Ma si ha un vantaggio complessivo, poiché la perdita è limitata come in tutte le trasformazioni in rango, e si ottiene il beneficio, con l’ultima trasformazione in valori z, di una distribuzione di forma esattamente normale che ha potenza maggiore di una distribuzione asimmetrica. Pertanto, quando la distribuzione dei dati originali è normale, la potenza è analoga a quella del corrispondente test parametrico.

 

Aree in una coda della curva normale standardizzata

 

                                                             

 

Distribuzione normale, per ricavare il valore di Z dal quantile P di probabilità.

 

 

 

 

 

Ma quando i dati originali hanno una forma molto lontana da quella normale, la potenza di questi test, misurata come efficienza asintotica relativa di Pitman (A. R. E. da Asymptotic Relative Efficieny), è maggiore di quella del test parametrico.

 

In altri termini,

-  quando i dati originali provengono da popolazioni distribuite normalmente con la trasformazione in ranghi si ha una perdita di efficienza asintotica relativa;

-  ma essa è evitata con la seconda trasformazione dei ranghi in valori normali.

Inoltre, aspetto più importante, i dati possono essere analizzati con i  metodi parametrici classici: test t di Student, test F.

 

Benché alla fine della trasformazione si utilizzino dati che hanno una distribuzione normale, i test che ricorrono al metodo dei normal scores sono classificati tra quelli non parametrici,

-  sia perché i dati iniziali non hanno distribuzione normale,

-  sia perché le conclusioni non sono influenzate dalla forma originaria dei dati e, come tutte le trasformazioni in ranghi, hanno poche assunzioni di validità.

Tuttavia quale tipo di statistica siano i normal score non vede tutti gli autori unanimi. E’ più facile dire che cosa  questi test non sono:

- non sono test esatti, in quanto utilizzano le distribuzioni asintotiche citate, fondate sulla normale;

- non sono distribution-free, in quanto infine hanno forma normale.

 

ESEMPIO (TRASFORMAZIONE DI DATI IN NORMAL SCORES). Dalla seguente serie di 5 misure,

11,5      8,8      9,1      8,4      24,2

 ricavare i normal-scores corrispondenti

 

Risposta. Il calcolo dei normal scores da dati di intervallo o di rapporto richiede alcuni passaggi logici:

1 –  ordinare i dati in modo crescente

8,4      8,8      9,1      11,5     24,2

2 - e sostituirli con i ranghi relativi

1        2        3        4        5

3 – Poiché N = 5, mediante la relazione

 dai singoli ranghi si ricavano i quantili

 

 

 

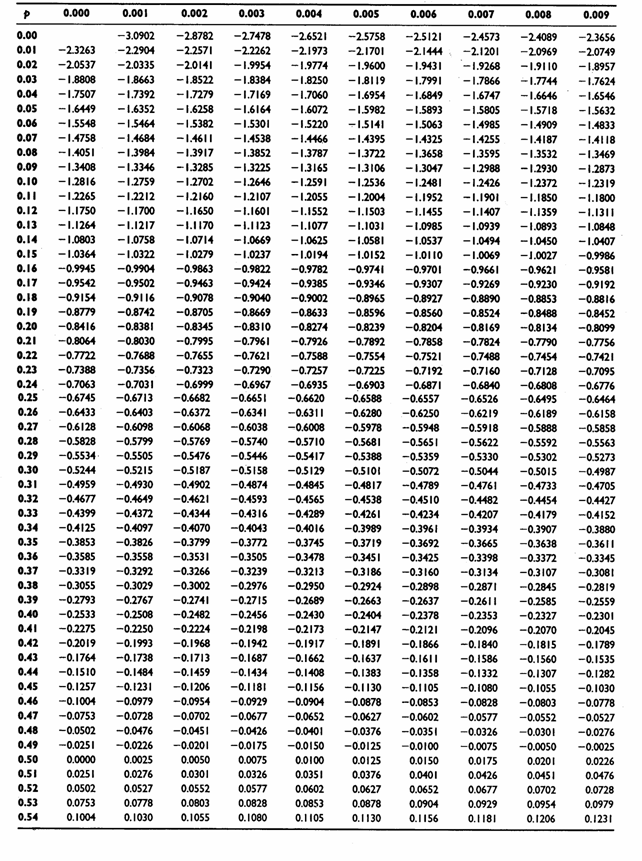
 4 – Attraverso la tabella della distribuzione normale, dal quantile o proporzione P si ottiene il valore di Z corrispondente.

In una distribuzione normale unilaterale, come nella tabella riportata, 

-  P = 0,167 (da rilevare entro la tabella e come valore più vicino) corrisponde a Z = 0,97 (approssimativamente e da ottenere sommando la riga con la colonna che danno la posizione della probabilità P individuata); poiché è collocato nella coda sinistra della distribuzione, il valore è negativo e quindi Z =  -0,97;

-  P = 0,333 corrisponde a Z = 0,43 (approssimativamente); poiché è nella coda sinistra della distribuzione è Z =  -0,43;

-    P  =  0,500 corrisponde a Z = 0,00.

-  Con P = 0,667 (poiché supera la metà) occorre calcolare la probabilità nella coda destra della distribuzione; quindi si ottiene P = 1 – 0,667 = 0,333. Ad essa corrisponde Z = +0,43.

-   Con P = 0,833 occorre calcolare la probabilità nella coda destra: P = 1 – 0,833 = 0,167. Ad essa corrisponde Z = +0,97.

 

La trasformazione dei quantili in valori Z determina la seguente serie

 

 

Per rendere più semplice e rapida questa ultima sostituzione delle P in Z_P, senza incorrere nelle imprecisioni determinate dalle approssimazione, in vari testi di statistica applicata sono riportate tabelle che permettono di ricavare il valore di Z direttamente dal quantile P di probabilità.

Ad esempio, utilizzando le ultime tabelle riportate, da P = 0,167 (leggendo 0,16 sulla riga e 7 nella colonna) si ricava Z_P = -0,9661 e da P = 0,677 si ricava Z_P = 0,4593.

Pertanto, valori più precisi di Z_P, da utilizzare al posto dei dati originali, sono

 

 

Come evidenzia la semplice lettura, i valori di Z_P, sono distribuiti in modo normale e con simmetria perfetta rispetto al valore centrale 0, quando non esistono ties. E’ una verifica che può essere fatta con semplicità, poiché la somma dei normal scores dovrebbe essere uguale a zero Tuttavia, quando essi sono in numero ridotto, l’allontanamento dalla normalità e dalla simmetria è limitato. Pertanto, come negli esempi sviluppati  nel paragrafo successivo, l’uso dei normal scores con un numero limitato di ties è ugualmente accettato.

 

Tra le tante varianti proposte, una seconda metodologia (in verità riportata da pochissimi testi), che permette di normalizzare la distribuzione di un campione casuale di dati di forma qualsiasi, è la Random Normal Deviates. La prima citazione di questo metodo appare su un articolo di J: Durbin del 1961 Some methods of constructing exact test, pubblicato su Biometrika, Vol. 48, pp. 41-55.

La serie originale di k osservazioni come ad esempio

11,5      8,8      9,1      8,4      24,2

 

1 – inizialmente è ordinata in modo crescente

8,4      8,8      9,1      11,5     24,2

 

2 - Successivamente, da un tabella di valori Z come l’ultima presentata che ne contiene 1000, per estrazione casuale si sorteggiano altrettanti valori di Z con il loro segno, come ad esempio

+0,0401     -1,0581     -0,8345     +0,3505     +1,2004

 

3 – Considerando il segno, i k valori Z sono ordinati dal minore al maggiore

-1,0581     -0,8345     +0,0401     +0,3505     +1,2004

 e i valori originali vengono sostituiti da questi, tenendo in considerazione il rango come nella tabella

 

 

Il minore dei valori Z (-1,0581) sostituisce la minore delle misure raccolte (8,4), mentre il secondo valore Z (-0,8345) sostituisce la seconda misura osservata (8,8),  ecc. …

Si ottiene uno pseudo normal sample, da cui l’altro nome di questo metodo.

 

La distribuzione campionaria dei valori Z è normale, in quanto estratta casualmente da una popolazione con distribuzione normale. Questa metodologia ha avuto poco seguito a causa delle incongruenze o contraddizioni logiche dei risultati. Infatti gli inconvenienti sono gravi:

-  ogni  estrazione campionaria ovviamente fornisce una serie differente di k valori Z,

-  ne deriva che la media e la varianza campionaria di ogni estrazione non sono uguali,

-  quindi a partire dalle stesse k osservazioni i test sulla media e sulla varianza potranno dare risultati statisticamente differenti e conclusioni contrastanti per la significatività.

 

Non utilizzata nell’inferenza, questa tecnica permette analisi teoriche interessanti sulla potenza di test fondati sui normal scores e permette di stimare probabilità esatte (come evidenzia il titolo dell’articolo di Durbin).

 

Una terza metodologia che ricorre ai valori di Z è l’Expected Normal Scores. I test che la utilizzano spesso sono chiamati “normal scores tests”, generando qualche equivoco con la prima metodologia. Proposta da M. E. Terry nel 1952 con l’articolo Some rank order tests which are most powerful against specific parametric alternatives (pubblicato su The Annals of Mathematical Statistics, vol. 23, pp. 346-366) e da W. Hoeffding nel 1951 con l’articolo “Optimum” nonparametric tests (pubblicato su Proc. 2^nd Berkeley Symp., pp. 83-92) permettono di ottenere un nuovo tipo di scores che fanno riferimento alla media di Z e quindi superano i limiti della Random Normal Deviates sulla variabilità dei risultati. Questi Expected Normal Scores sono reperibili in alcuni testi di tabelle, pubblicate tra le fine degli anni ’50 e i primi anni ’60. Tra questi,

-  il volume di R. A. Fisher e F. Yates del 1957 Statistical Tables for Biological, Agricultural and Medical Research  (5^th ed. Oliver & Boyd, Edinburgh), che forniscono i valori per  £ 50.

-  quello di E. S. Pearson e H. O. Hartley del 1962 Biometrika Tables for Statisticians (Vol. I, 2^nd ed. Cambridge University Press, Cambridge, England),

-  quello di D. B. Owen del 1962 Handbook of Statistical Tables (Addison-Wesley, Reading, Mass.). Questo tipo di procedura è ancora basato sui tanghi delle osservazioni e pertanto è un test non parametrico

I test che utilizzano questa trasformazione sono chiamati Normal Scores test di Fisher-Yates; in altri testi, come quello di Hollander, test di Fisher-Yates-Terry-Hoefdding.

Tra queste differenti metodologie (Normal Scores, Random Normal Deviates, Expected Normal Scores), quella di van der Waerden è la più diffusa e proposta nei programmi informatici.