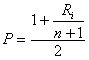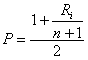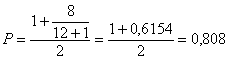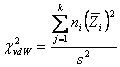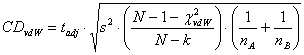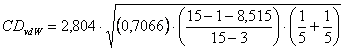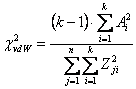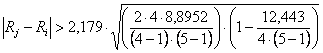ALTRI METODI INFERENZIALI:

NORMAL SCORES E RICAMPIONAMENTO

 

 

 

22.2.  APPLICAZIONI DEI NORMAL SCORES DI VAN DER WAERDEN AI TEST SULLA MEDIANA PER UNO, DUE E PIU’ CAMPIONI

 

 

La trasformazione di van der Waerden può essere applicata in test che utilizzano

-  sia metodi non parametrici,

-  sia metodi parametrici

 per testare ipotesi sulla tendenza centrale, che in questo caso è la mediana. Trattandosi di dati che hanno avuto una trasformazione in ranghi, quindi hanno perso l’informazione della scala a intervalli o di rapporti, sono sempre classificati tra i test non parametrici, anche se con la trasformazione successiva in normal scores acquisiscono sempre la forma normale. In teoria, è sempre richiesto che non esistano ties, in quanto la loro presenza rende la distribuzione asimmetrica. Tuttavia, come negli esempi successivi tratti da testi a grande diffusione internazionale, la loro presenza è ugualmente accettata, con la giustificazione che i test sono robusti e l’allontanamento dalla normalità è limitata. Sono gli stessi concetti illustrati nel capitolo sui test non parametrici per un campione, nel quale è dimostrato come l’effetto sulle probabilità sia ridotto.

I vari esempi di applicazione riportati in letteratura riguardano casi con

A - un campione, sia con test di permutazione, sia con distribuzione Z

B - due campioni dipendenti e indipendenti, con distribuzione Z e distribuzione

C - k campioni indipendenti, con distribuzione ; dopo il rifiuto dell’ipotesi nulla, è possibile applicare test per confronti multipli a posteriori

D – k campioni dipendenti, con distribuzione .

 

 

ESEMPIO 1  (PER UN CAMPIONE, CON TEST DI PERMUTAZIONE). Per un campione, può essere utile seguire l’applicazione presentata da P. Sprent e N. C. Smeeton nel testo del 2001 Applied Nonparametric Statistical Methods (3^rd ed. Chapman & Hall/CRC, London, 982 p.), sviluppando in modo dettagliato tutti i passaggi logici, che nel testo sono appena accennati. Esso utilizza il test di casualizzazione per un campione o permutation test di Fisher-Pitman; ma, essendo fondato sui ranghi, fornisce risultati del tutto analoghi al test T di Wilcoxon.

 

Disponendo di una serie di 12 tassi d’accrescimento di popolazioni batteriche,

78    49    12    26    37    18    24    108    49    42    47    40

 si vuole verificare l’ipotesi nulla sulla mediana

H₀: me £ 30

 contro l’ipotesi alternativa

H₁: me > 30

(nel testo Sprent e Smeeton scrivono, come molti autori,   H₀: q = 30   contro   H₁: q > 30)

 

Risposta. La serie di trasformazioni dei dati originari, riportate nelle righe della tabella successiva, richiede che

 

1 - i dati osservati siano ordinati per rango (come nella prima riga);

 successivamente, ad ogni dato osservato deve essere sottratta la mediana indicata nell’ipotesi nulla

H₀: Me = 30

 

2 - ricavando altrettante (N = 12) differenze (come nella riga 2).

 

3 - Queste differenze a loro volta devono essere ordinate per rango k (come nella riga 3),

 

4 – per ottenere la trasformazione in quantili (P), prima come rapporto P =   (riga 4)  e successivamente con il calcolo della relazione (riga 5).

 

 

 

 

 5 –Ottenuti i quantili (P) corrispondenti a ogni rango (riga 5), attraverso la tabella riportata nelle pagine precedenti, si trasformano i quantili P in valore Z (riga 6).

 6 – La prima metà dei valori Z è negativa e l’altra metà è positiva, con valori distribuiti in modo esattamente simmetrico intorno allo zero (riga 6).

Tuttavia, poiché nell’operazione successiva è necessario che tutti i valori siano positivi, si aggiunge una costante; fino a circa 700 dati, questa costante può essere 3 (infatti con un campione di queste dimensioni nessun quantile ha un valore Z inferiore a –3).

 

 7 – Aggiungendo 3, si ottiene una serie di valori tutti positivi (riga 7), che hanno gli stessi ranghi e mantengono le stesse distanze tra i valori della serie precedente; è una caratteristica importante, per il successivo test di significatività, fondato sulle somme di questi valori.

 

 8 – A ogni valore della ultima serie di valori Z (riga 7), si assegnano gli stessi  segni delle differenze ordinate per ranghi (riportate nella riga 3): si ottengono i dati (riga 8) per il test di permutazione.

 

Per la verifica delle ipotesi formulate, sulla ultima serie di dati semplificata con arrotondamento a due decimali per facilitare le operazioni,

 

 

 si applica il permutation test o test di Pitman.

Se fosse vera l’ipotesi nulla (H₀: me = 30), ogni valore può essere indifferentemente positivo oppure negativo e la somma tendere a 0. Con N = 12, il numero di risposte possibili è

2¹² = 4096

 

E’ possibile ordinare queste 4096 possibili risposte, iniziando da quella che fornisce la somma maggiore, formata da valori tutti positivi, e finendo che quella che fornisce la somma minore, formata da valori tutti negativi.

 

Con un campione di queste dimensioni, il calcolo può essere effettuato ricorrendo a un programma informatico. Secondo Sprent e Smeeton, in un test unilaterale corrisponde una probabilità P = 0,062 che non permette di rifiutare l’ipotesi nulla, anche se può essere interpretato come tendenzialmente significativo: il campione è relativamente piccolo e quindi con un esperimento con numero maggiore di dati potrebbe risultare significativo.

I due autori pongono in evidenza il fatto che il test di Pitman sui dati originali dopo sottrazione di 30

 

 

 forniva una probabilità P = 0,0405 esattamente uguale al test di Wilcoxon, ovviamente sempre in un test unilaterale. In entrambi un risultato più significativo di quello ottenuto con questa trasformazione di wan der Waerden; leggermente migliore anche del test t di Student che stima P = 0,0462 a causa dell’asimmetria destra generata dal valore +78.

Sprent e Smeeton commentano che questo risultato è fuori linea con l’esperienza comune, la quale dimostra che questo test differisce poco dal test di Wilcoxon.

Anche con i normal scores di van der Waerden è possibile stimare l’intervallo di confidenza; ma i risultati appaiono meno soddisfacenti di quelli del test di Pitman e del test di Wilcoxon.

 

ESEMPIO 2  (CON GLI STESSI DATI PRECEDENTI, PER UN CAMPIONE CON TEST Z) Il metodo, citato da C. van Eeden nell’articolo del 1963 The relation between Pitman’s asymptotic relative efficiency of two tests and the correlation coefficient between their test statistics (pubblicato su Annals of Mathematical Statistics, Vol. 34, pp. 1442-1451), è sinteticamente riportato nel testo di W. J. Conover del 1999 Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.). E’ fondato sul calcolo dei quantili e sull’uso della distribuzione normale.

Dopo aver calcolato

-  la somma dei normal scores con il loro segno

 - la somma dei quadrati dei normal scores

 stima

 

dove T è distribuito in modo approssimativamente normale.

La probabilità P del test è ricavata  dal valore Z = T, nella tabella normale standardizzata, ricorrendo a quella unilaterale oppure bilaterale in funzione dell’ipotesi.

 

Disponendo della stessa serie precedente di 12 tassi d’accrescimento,

78    49    12    26    37    18    24    108    49    42    47    40

 verificare l’ipotesi nulla sulla mediana

H₀: me £ 30

 contro l’ipotesi alternativa

H₁: me > 30

 

Risposta. La procedura è illustrata nei suoi passaggi logici, riportati nella tabella successiva.

I dati osservati

 1 - sono riportati nella prima colonna; non è necessario ordinarli in modo crescente;

 2 – successivamente ad ogni dato osservato si sottrae il valore riportato nell’ipotesi (30), ottenendo la serie di differenze (colonna 2);

 3 – a ogni differenza , considerata in valore assoluto, si attribuisce il rango  di  (colonna 3);

 4 – per ogni rango (), si stima il quantile  (colonna 4)

 con

 dove  è il numero di ranghi, escludendo le differenze uguali a 0. In questo caso, nessuna differenza  è uguale a 0; quindi  = 12. E’ una trasformazione che rende tutte le probabilità P > 0,5.

Ad esempio, nel caso del rango riportato nella prima riga (= 11),

 il calcolo è

 

 

 5 – Dalla quantili  (colonna 4), attraverso la tabella riportata nel paragrafo precedente si ricavano i valori di (colonna 5), che sono sempre positivi, in quanto con la formula precedente si ottiene sempre  > 0,5.

 6 – I valori di  (colonna 6), sono ottenuti attribuendo a ogni  (colonna 5) il segno della differenza  (colonna 4).

 7 – Si perviene gli  (colonna 7), elevando al quadrato i valori  (colonna 6).

 8 – Infine con

= 5,6701      e        = 9,8277

 si stima

 =

 

9 – Il valore di  ha una distribuzione approssimativamente normale. Nella tabella della distribuzione normale, che deve essere unilaterale in base alla domanda espressa in questo esempio, a Z = 1,81 corrisponde la probabilità P = 0,0351.

Il test di permutazione di Pitman forniva la probabilità esatta P = 0,0405 mentre la probabilità asintotica qui calcolata con la distribuzione Z  è P =  0,0351. E’ molto vicina, ma inferiore; potendo scegliere, sarebbe più corretto utilizzare la metodologia di Pitman, poiché questa probabilità minore è l’effetto di una stima asintotica, che rende il test più significativo di quanto sia il realtà.

Per la scelta del test, con pochi dati è meglio utilizzare Pitman. All’aumentare del loro numero, le due probabilità P tendono a convergere; inoltre il test di Pitman diventa praticamente inapplicabile. Tuttavia, rispetto a questi due, di norma la preferenza è attribuita al test di Wilcoxon per un campione.

 

ESEMPIO 3  (PER DUE CAMPIONI DIPENDENTI, CON TEST Z) . Si vuole confrontare se la somministrazione con il cibo di dosi minime di una sostanza tossica (pesticidi clorurati) a cavie per un mese determina un aumento della quantità presente nel sangue.

A questo scopo, l’analisi di 13 cavie ha fornito i seguenti valori

 

 

 

Si vuole valutare se, come atteso, si è realizzato un aumento significativo.

Risposta. E un test unilaterale, con il quale si vuole testare l’ipotesi nulla

H₀: d £ 30

 contro l’ipotesi alternativa

H₁: d > 30

Visto il tipo di scala (quantità in mg/l), si potrebbe utilizzare il test t di Student. Ma nella realtà della pratica sperimentale, soprattutto con pochi dati, il rispetto delle condizioni di validità non è assicurato. In particolare, quando si studia una sostanza nuova, come afferma Jerome Klotz nel suo articolo del 1963 Small sample power and efficiency for the one sample Wilcoxon and normal scores test (pubblicato su The Annals of Mathematical Statistics, Vol. 34, pp.624-632): “ Because of the extremely high efficiency of the non-parametric tests relative to the t region interest, it is the author’s opinion that the non-parametric tests would be preferred to the t in almost all pratical situations”.

Confrontando il metodo dei normal scores prima con il test t di Student e poi con il test T di Wilcoxon, Klotz indica la sua preferenza per questo ultimo, anche se le differenze nei risultati sono in realtà trascurabili: ”The normal scores test althouhg most powerful locally and usually more powerful in the region covered (rispetto al test t) becomes less powerful for large shift when compared to the Wilcoxon. In any case for the sample sizes covered the difference in power in somewhat academic.”

 

Ritornando all’ipotesi, è utile ricordare che

-  con il test parametrico l’ipotesi riguarda la media delle differenze,

-  con un test non-parametrico l’ipotesi riguarda la mediana delle differenze.

In modo del tutto analogo al test per un campione,

 1 – dalle due serie di dati accoppiati (colonna 1), si ricava la serie di differenze  con il loro segno (colonna 2);

 

 

 

 2 – Successivamente, considerando le differenze  in valore assoluto, devono essere riportati i ranghi  di  (colonna 3), con esclusione delle differenze nulle  = 0, che vengono ignorate in tutti i calcoli successivi non fornendo indicazioni sulla direzione della differenza.

 

 3 – Per ogni rango (), si stima il quantile  (colonna 4)

 mediante la relazione

 

 dove  è il numero di ranghi (sempre escludendo le differenze = 0).

In questo caso, c’è una  = 0 (cavia F); quindi  = 12.

Ad esempio, nel caso del rango riportato nella seconda riga ( =  8),

 il calcolo è

 arrotondato alla terza cifra decimale.

 

 4 – Dai quantili  (colonna 4) attraverso la tabella riportata nel paragrafo precedente si ricavano i valori di  (colonna 5) che sono sempre positivi, in quanto  > 0,5.

 

 5 – I valori di  (colonna 6), sono ottenuti attribuendo a ogni  (colonna 5) il segno della differenza  (colonna 2).

 

 6 – Si perviene gli  (colonna 7), elevando al quadrato i valori  (colonna 6)

 

7 – Infine con

= 6,3074      e        = 9,8806

 si stima

 

 =

 

9 – Il valore di  ha una distribuzione asintoticamente normale. Nella tabella della distribuzione normale ridotta Z, che deve essere unilaterale in base alla domanda espressa in questo esempio, a Z = 2,00 corrisponde la probabilità P = 0,0228. Si rifiuta l’ipotesi nulla.

 

Questo risultato può essere confrontato con quello ottenuto dal test di Wilcoxon e quello ottenuto dal test di permutazione di Fisher-Pitman sui dati originali (riportati nel capitolo sui test non parametrici per due campioni dipendenti).

Inoltre, come nell’esempio per un campione, è possibile effettuare il test di permutazione sui normal scores delle differenze.

 

 

ESEMPIO 4 (PER DUE CAMPIONI INDIPENDENTI CON TEST c² E TRASFORMAZIONE IN Z; PERMUTATION TEST DI FISHER-PITMAN).  L’esempio è tratto, con modifiche, dal testo di David J. Sheskin, 2000, Handbook of Parametric and Nonparametric Statistical Procedures (2^nd ed. Chapman & Hall/CRC, London, 982 p.).

Per valutare l’efficacia di un antidepressivo, sono stati campionati 10 pazienti giudicati clinicamente depressi. In un esperimento a doppio cieco (il paziente e il medico che visita non sanno se hanno assunto il farmaco o il placebo, che è stato somministrato da un altro medico), per 6 mesi a 5 di essi è stato somministrato il farmaco e agli altri 5 il placebo. Dopo 6 mesi, lo psichiatra ha assegnato un test, ottenendo i seguenti punteggi (più alti per i pazienti più depressi)

 

 

 

 

Il farmaco è stato efficace?

Risposta. Innanzi tutto è importante annotare che la scala è discreta e che i punteggi uguali sono relativamente frequenti, dati i pochi casi. Nonostante questa alta presenza di bias, l’autore propone ugualmente l’uso dei normal scores, il cui analogo non parametrico è il test U di Mann-Whitney.

 

La procedura richiede una serie di passaggi logici.

 1 – Tenendo separati i punteggi dei due gruppi (colonna 1 e 2), a ogni valore viene assegnato il rango  (colonna 3) considerando i due gruppi come se fossero uno solo.

 

 2  - Successivamente per ogni rango ,

 attraverso la relazione

 dove N è il numero totale di dati (N = 10)

 viene calcolato il quantile  (colonna 4)

 

 3 - Attraverso le tabelle riportate nel paragrafo precedente, si trasformano le  in , mantenendo l’informazione di gruppo: i due gruppi di dati originali (colonna 1 e 2) sono quindi trasformati in normal scores (rispettivamente colonna 5 e 6)

 

 

 

 4 – Si calcolano i totali dei due gruppi di normal scores, ottenendo

-  per il gruppo del farmaco  = -2,2408 (colonna 5) e la media  = - 0,448

-  per il gruppo del placebo  = +2,1634 (colonna 6) e la media  = + 0,433

 

 5 -  Si elevano al quadrato i vari  dei due gruppi, ottenendo la colonna dei  (colonna 6) e la loro somma  = 5,5179

 

 6 – Si applica la formula generale per stimare

 il c² di van der Waerden

 dove

 -  è distribuito come il  con gdl k-1; nel caso di due campioni indipendenti gdl = 1

 -  è ricavato da

Con i dati dell’esempio,

 si ottiene c² = 3,166 con gdl = 1.

 

Se il test è bilaterale, i valori critici riportati nella tabella con gdl = 1

- per a = 0.05 è c² = 3,841

- per a = 0.01 è c² = 6,635

 

Se il test è unilaterale, si devono prendere i valori riportati rispettivamente per  a = 0.10  e  a = 0.02 (questo ultimo raramente riportato nelle tabelle dei testi di statistica)

Quindi per un test unilaterale, i valori critici

-- per a = 0.05 è c² = 2,706

 

 7 - Poiché il test dell’esempio è unilaterale, il risultato  permette di rifiutare l’ipotesi nulla con probabilità P < 0.05.

 

 8 – In assenza dei valori critici del c², ma solamente con gdl = 1, per probabilità particolari è possibile utilizzare i valori Z corrispondenti, a causa della relazione

Ad esempio, in test unilaterali

- per a = 0.05 si ha Z = 1,96 quindi  Z² = (1,96)² = 3,841  e   c² = 3,841

- per a = 0.01 si ha Z = 2,328 quindi  Z² = (2,328)²  = 5,419   e  c² = 5,419

E’ possibile anche fare il cammino opposto, verificando la significatività con Z

 a causa della relazione

 

 9 – Il valore calcolato c² = 3,166 con gdl = 1 equivale a  Z =  = 1,78.

Nella distribuzione normale unilaterale a  Z = 1,78 corrisponde la probabilità P = 0,0375. E’ una risposta più precisa di quanto si possa ottenere con la tavola sinottica del chi- quadrato, la quale riporta solamente alcuni valori critici.

 

Nel testo di P. Sprent e N. C. Smeeton del 2001 Applied Nonparametric Statistical Methods (3^rd ed. Chapman & Hall/CRC, London, 982 p.), è proposto l’uso del test di casualizzazione o permutation test di Fisher Pitman per due campioni indipendenti, dopo che i dati originali siano stati trasformati in random scores. Con  dati nel gruppo minore e  dati in quello maggiore, il numero di combinazioni possibili è

Ovviamente con calcoli manuali il test può essere applicato solo nel caso di piccoli campioni.

Nell’esempio precedente, con  = 5  e   = 5, il numero di risposte possibili è

E’ un numero che rende fattibile il calcolo manuale; ma in questo caso si pone il problema dei ties.

Appare quindi preferibile il metodo precedente.

 

ESEMPIO 5 (ANOVA A UN CRITERIO CON TEST c²). L’esempio è tratto, con modifiche, dal testo di David J. Sheskin del 2000, Handbook of Parametric and Nonparametric Statistical Procedures (2^nd ed. Chapman & Hall/CRC, London, 982 p.).

Uno psicologo intende valutare se il rumore ostacola l’apprendimento. A questo scopo, per estrazione casuale, ha separato 15 soggetti in 3 gruppi. Il primo gruppo è stato messo in una stanza silenziosa; il secondo gruppo in condizioni di rumore moderato, come il suono di musica classica; il terzo in una stanza con rumore molto alto, trasmettendo musica rock. Ogni individuo ha avuto 20 minuti di tempo, per memorizzare 10 parole prive di senso. Il giorno dopo, ogni soggetto ha scritto le parole che ricordava.

Il numero di parole scritte correttamente sono state

 

 

Il rumore ostacola l’apprendimento?

 

Risposta. La quantità si parole memorizzate correttamente può esser espresso con un numero, come in questo caso, oppure come proporzione o percentuale sul totale. Poiché il metodo prevede la trasformazione dei dati in ranghi, il risultato è identico.

Per verificare l’ipotesi nulla

H₀:  me₁ = me₂ = me₃

 contro l’ipotesi alternativa

H₁: almeno due mediane sono diverse tra loro

 il test richiede la seguente serie di passaggi logici e metodologici:

 

 1 -  Ordinare i dati in modo crescente, mantenendo l’informazione di gruppo, come nelle prime tre colonne (l’ordine tra gruppi è ininfluente).

 2 – Attribuire il rango, dando valori medi uguali ai ranghi uguali (colonna 4); è possibile osservare che in questo esempio (di Conover) i ranghi uguali sono molti, anche se vari autori per una applicazione corretta del test richiedono che i ties siano assenti o molto limitati.

 3 - Per ogni rango , attraverso la relazione

 dove N è il numero totale di dati (N = 15)

 calcolare il quantile  (colonna 4).

 4 – Ricorrendo alla tabella riportata nel paragrafo precedente, trasformare i quantili  in valori , mantenendo l’informazione del gruppo di appartenenza: i tre gruppi di dati originali (colonne 1, 2, 3) sono quindi trasformati in normal scores (rispettivamente colonne 6, 7, 8)

 

 

 5 – Calcolare il totale dei normal scores di ogni gruppo, ottenendo

-  per il gruppo 1,  = +4,4220 (colonna 6) e la media  = + 0,8844

-  per il gruppo 2,  = -1,6136 (colonna 7) e la media  = - 0,3227

-  per il gruppo 3,  = -2,8148 (colonna 8) e la media  = - 0,5630

 

 6 - Elevare al quadrato i valori  unendo i tre gruppi; si ottiene la colonna dei  (colonna 9) e la loro somma è  = 9,8927

 

 7 –  Per stimare il c² di van der Waerden

 applicare la formula

 dove

 -  è distribuito come il  con gdl = k-1; nel caso di due campioni indipendenti gdl = 2

 -  è dato da

 ( come evidenzia Conover).

Con i dati dell’esempio,

dove

 e

 

 si ottiene c² = 8,515 con gdl = 2.

 

Con più gruppi come nell’esempio, il test è ovviamente bilaterale. I valori critici, riportati nella tabella  del c² con gdl = 2, sono

- per a = 0.05 è c² = 5,991

- per a = 0.025 è c² = 7,378

- per a = 0.01 è c² = 9,210

Poiché il valore calcolato (8,515) si trova tra a = 0.025  e  a = 0.01 si rifiuta l’ipotesi nulla con probabilità P < 0.025: esiste una differenza significativa tra almeno due delle tre mediane. La conclusione, come in quasi tutti i test non parametrici verte sulla mediana dei dati originali, anche se essa, come in questo esempio, non viene calcolata.

 

Per k campioni indipendenti, questo test risulta più potente del test della mediana e ha una potenza simile, ma forse leggermente inferiore, al test di Kruskal-Wallis.

 

 

ESEMPIO 6. (CONFRONTI MULTIPLI A POSTERIORI, IN K CAMPIONI INDIPENDENTI).  L’esempio, che utilizza gli stessi dati del precedente, è tratto con modifiche dal testo di David J. Sheskin del 2000, Handbook of Parametric and Nonparametric Statistical Procedures (2^nd ed. Chapman & Hall/CRC, London, 982 p.) e dal testo di W. J. Conover del 1999, Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.).

Se, con il test precedente, si è rifiutata l’ipotesi nulla

H₀:  me₁ = me₂ = … = me_k

 contro l’ipotesi alternativa

H₁: almeno due mediane sono diverse tra loro

 è possibile verificare tra quali coppie di mediane le differenze risultano significative.

In realtà, il metodo richiede che il confronto sia effettuato sulle medie dei normal scores. Il metodo che è riportato più frequentemente nei testi è fondato sulla differenza minima significativa

 con

 dove

-   = numero totale di dati e  =  numero di gruppi

-   =  valore del t di Student, in una distribuzione bilaterale con gdl =    e a = a_T/C

-  con C = numero confronti, secondo il principio del Bonferroni o Bonferroni-Dunn,

-   = valore del  c² calcolato nel test, che ha permesso di rifiutare l’ipotesi nulla alla probabilità a

-   e  = numero di dati nei due campioni a confronto

 

Con i dati dell’esempio precedente, dove

-  per il gruppo 1, la media  = + 0,8844

-  per il gruppo 2, la media  = - 0,3227

-  per il gruppo 3, la media  = - 0,5630

-   = 8,515     = 15      = 3       = 5      = 5

-   =  = 0,7066

-  per a_T = 0.05 si ha a = 0.05/3 = 0.0167 poiché i confronti tra le tre medie sono 3

-  = 2,75 per la probabilità comparison-wise a =  0.0167 con gdl = 12 .

Il valore di  per tale probabilità è riportato raramente nelle tabelle; ma può essere stimato per interpolazione lineare. Nel caso dell’esempio, con gdl = 12

-  tra il valore  = 3,055  alla probabilità a =  0.01

-  e il valore  = 2,681  alla probabilità a =  0.02

 si ottiene  = 2,804

 

La differenza minima significativa, poiché i tre gruppi sono bilanciati con n = 5,

 

 

 

 risulta  = 1,008.

Poiché ogni differenza  tra coppie di medie che sia risulta significativa alla probabilità experiment-wise  = 0.05, con i dati dell’esempio è significativa

- sia la differenza tra il gruppo 1 e il gruppo 2

- sia la differenza tra il gruppo 1 e il gruppo 3

- ma non la differenza tra il gruppo 2 e il gruppo 3

Quando i campioni non sono bilanciati, quindi in un confronto   e  sono differenti, il calcolo della differenza minima significativa  deve essere ripetuto.

 

 

ESEMPIO 7. (ANOVA A DUE CRITERI CON TEST c² E CONFRONTI MULTIPLI). Analogo al test di Friedman e con una potenza molto simile, questo test è illustrato sinteticamente nel testo di W. J. Conover del 1999, Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.).

Si assuma che in 5 zone di una città per 4 giorni siano state calcolate le quantità medie delle polveri Pm 10, ottenendo la seguente serie di dati

 

 

 

Esiste una differenza significativa nella presenza media di polveri tra le 5 zone?

 

Risposta. Trattandosi di medie, non è possibile utilizzare il test parametrico; inoltre si ha una evidente differenza tra le varianze. Anche se i dati sono riportati in un tabella a doppia entrata (zona e giorni), come nel test di Friedman l’ipotesi da verificare può riguardare solamente un fattore.

In questo caso, la domanda riguarda la differenza tra le zone:

H₀: me_A = me_B = me_C = me_D = me_E

 

Se riguardasse i giorni, il metodo sarebbe identico, ma scambiando righe e colonne.

 

1 - Dopo aver trasformato i dati nei ranghi  entro ogni singola riga, con n righe e k colonne si ottiene

 

 

 

2 – Mediante la relazione

 si stimano i quantili

 

 

 3 - Attraverso le tabelle riportate nel paragrafo precedente, si trasformano le  in valori ,

 

 

 

 e si calcolano i totali di ogni colonna (), i loro quadrati () e la loro somma,

ottenendo

= 27,6711

4 - Successivamente ogni valore  è elevato al quadrato ()

 

 

 

 e la loro somma totale, per k gruppi e n repliche, è

 = 8,8952   e   rappresenta la varianza s².

 

5 – Infine mediante il rapporto

 

 si calcola , che è distribuito come un c² con gdl = k-1.

Con i dati dell’esempio

 si ottiene  = 12,443.

Poiché nella tabella dei valori critici del c²  con gdl = 4 per

-  a = 0.05  si ha c² = 9,488

-  a = 0.025  si ha c² = 11,143

-  a = 0.01  si ha c² = 13,277

 si rifiuta l’ipotesi nulla con probabilità P < 0,025.

 

Secondo Conover, a differenza di quanto evidenziato nel test di Friedman, l’approssimazione del risultato al valore del c² con gdl = k-1 è sufficientemente buona. Di conseguenza non è richiesto, anche se possibile e accettato ma meno potente, l’uso del test F con gdl n₁ = k-1 e  n₂ = (k-1)×(n-1). Esso è notevolmente più cautelativo o prudenziale; infatti, sempre in una distribuzione bilaterale, per

-  a = 0.05  si ha F_(4,3) = 15,1.

 

Rifiutata l’ipotesi nulla, si pone il problema di verificare tra quali mediane esista una differenza significativa, alla probabilità experiment-wise a_T prefissata.

Il confronto utilizza il totale dei ranghi (R) dei k gruppi

 

 

 dove la  t di Student ha gdl = (k-1)×(n-1) alla probabilità experiment-wise a_T prefissata.

Con i dati dell’esempio

 

 

 dove

-  per la probabilità a = 0.05 bilaterale e gdl = (5-1)×(4-1) = 12 si ha t = 2,179

-  k = 5    n = 4      = 12,443      = 8,8952

 si ottiene

 

che la differenza minima significativa tra due somme dei ranghi è uguale a 2,50

Pertanto, ordinando le somme dei ranghi dalla maggiore alla minore e con una rappresentazione grafica sintetica

B    A    D    C    E

19   17   10    7    7

 

non risultano significative solo le differenze tra le somme dei ranghi 

-  tra B e A

-  tra C e E.

 

 

 

A livello di interpretazione dei dati, questa conclusione è da trasferire alle mediane dei dati originali.

In altri testi si propone l’uso delle medie dei ranghi (), con metodi leggermente più lunghi.