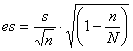IL DISEGNO SPERIMENTALE:

CAMPIONAMENTO, PROGRAMMAZIONE DELL’ESPERIMENTO E POTENZA

 

 

23.4.   I PARAMETRI IMPORTANTI PER IL CAMPIONAMENTO

 

 

Per procedere in modo corretto all’estrazione di un campione da una popolazione, è necessario che siano realizzate due condizioni preliminari:

1 -  la popolazione deve essere divisa in unità chiaramente distinguibili, chiamate sampling units;

2 -  deve essere disponibile una lista completa di tutte le unità che formano la popolazione.

Di conseguenza, tutte le unità della popolazione devono essere precedentemente definite e numerate in modo chiaro. Ma spesso questa operazione incontra ostacoli. Ad esempio, per quantificare il consumo dei vai tipi di anticrittogamici o di concimi in agricoltura, occorrerebbe conoscere tutte le aziende che ne fanno uso. Ma non è semplice ottenere questo elenco, per una provincia o una regione intera.

Una soluzione potrebbe essere la suddivisione del territorio in quadrati. Successivamente, si procede al campionamento di alcune aree, cercando tali aziende entro esse.

Rispetto a un censimento completo condotto da un ricercatore esterno, è un’operazione molto più economica e semplice, per la possibilità di analizzare in modo dettagliato ogni singolo territorio e per l’aiuto alla conoscenza esatta che molti operatori o contadini locali possono fornire.

Quando il territorio è suddiviso in unità di area, si parla di area sampling. A loro volta, le aree possono essere scelte sulla base di fattori di omogeneità, che non sono casuali. Ad esempio, aree di montagna, collina e pianura che sono caratterizzate da una differente tipologia di aziende agricole, da produzioni e modalità di conduzione differenti, per i quali è richiesto l’uso di anticrittogamici o concimi diversi. Si parla allora di cluster sampling.

 

Nel campionamento per area, è possibile seguire due strategie alternative:

-  scegliere poche aree grandi, ognuna con molte unità,

-  scegliere molte aree piccole, con poche unità.

Il criterio da seguire deve essere la precisione massima delle medie che saranno stimate. Quindi è migliore il metodo che determina una varianza minore, per il parametro rilevato sulle unità (come illustrato nel paragrafo precedente). Per una dimensione del campione prefissata, cioè per lo stesso numero di individui (aziende) da controllare, poche aree grandi forniscono una stima meno accurata (varianza maggiore) di molte aree piccole. Infatti le unità della stessa zona possono avere caratteristiche distintive rispetto a quelle delle altre zone, che determinano una coltivazione specializzata in un solo settore (esempio: vigneti in collina, riso in zone con alta disponibilità di acqua).

Ma non esiste uno schema generale, ugualmente valido per tutte le zone collinari o con disponibilità analoghe di acqua. Quindi il problema deve essere risolto sulla base dei dati reali, cioè delle informazioni acquisite sul campo, mediante un’analisi precedente o uno studio pilota.

 

Collegato al tipo di campionamento, un altro problema da risolvere è il numero di dati da raccogliere. Per definire con chiarezza questa quantità (), occorre considerare due parametri:

-  la precisione desiderata,

-  le risorse disponibili.

Anche in questo caso, la meta statistica è la precisione massima ottenibile con le risorse disponibili. Nei capitoli precedenti, sono state presentate le formule e le applicazioni ai vari test della stima di .

Come nell’esempio presentato in precedenza, il campionamento casuale semplice è appropriato quando la variabilità della popolazione è bassa, quindi non sono presenti gruppi con caratteristiche molto differenti.

 

Un altro concetto importante è la dimensione () del campione, in rapporto a quella () della popolazione. Nei capitoli precedenti, sono state presentate le formule di correzione della varianza o dell’errore standard in popolazioni finite, come

 

Nella loro utilizzazione, il concetto importante è che in una popolazione ampia l’errore standard dipende

-  principalmente dalle dimensioni di , 

-  solo secondariamente da quelle di .

Se si è stimato che il campione debba avere  = 100, è secondario che la popolazione sia  = 2.000 oppure  = 200.000.

Per vari autori, questa correzione può essere omessa quando  è inferiore al 10% di .

Infatti, in questa situazione, la correzione diminuisce il valore dell’errore standard al massimo di circa il 5% come evidenzia l’esempio di un campione di 30 unità su una popolazione complessiva di 300:

 

 = 0,949

 

Rispetto al campionamento casuale semplice (simple random sampling), il campionamento sistematico (systematic sampling) offre

1 - due vantaggi e

2 - due svantaggi potenziali.

 

1) Tra i vantaggi del campionamento sistematico, il più importante è la facilità di applicazione, poiché richiede l’estrazione di un solo numero casuale. Inoltre determina una distribuzione più regolare, quando si utilizza un elenco completo della popolazione. Per la sua semplicità, è diventata una tecnica popolare. Per le caratteristiche di regolarità nella scelta, fornisce stime più accurate di quelle del campionamento casuale semplice, con un miglioramento che a volte è statisticamente importante.

 

2) Tra gli svantaggi potenziali è da ricordare che, se nella popolazione sono presenti variazioni periodiche o cicliche che hanno la stessa lunghezza d’onda del campionamento, si può ottenere un campione gravemente alterato. Ad esempio, se si selezionano gli alberi in un bosco coltivato, dove sono disposti in modo regolare, con un campionamento sistematico potrebbe succedere di scegliere solo gli alberi collocati nella stessa riga oppure solo quelli vicini a un canale. Prima di decidere l’uso di un campione sistematico, è quindi conveniente conoscere la natura della variabilità presente nella popolazione.

Tra gli svantaggi importanti, è da ricordare soprattutto che non vi è modo di stimare l’errore standard con un campionamento sistematico, poiché le formule riportate si applicano a modelli casuali, non a distribuzioni che presentano regolarità ignote. Si può ricorrere vantaggiosamente alle formule presentate, quando il campionamento sistematico è parte di un piano di campionamento più complesso.

 

Il campionamento stratificato (stratified sampling) è vantaggioso quando la popolazione è molto eterogenea e può essere suddivisa in parti omogenee; cioè quando la varianza tra le parti è grande e la varianza entro le parti è piccola. Esso richiede tre fasi:

-  dividere la popolazione in parti, chiamate strati (strata),

-  scegliere un campione in modo indipendente entro ogni strato,

-  porre attenzione al calcolo della media, in particolare se essa deve essere indicativa di quella della popolazione e il numero di individui campionati entro ogni strato è differente da quello presente nella popolazione (come fatto per la stima del totale vero, nell’esempio di Snedecor e Cochran).

Poiché aree piccole spesso sono tra loro più omogenee di quelle grandi, per ottenere una stima più efficiente del valore reale della popolazione risulta vantaggioso scegliere un numero alto di aree piccole, piuttosto che poche aree grandi.

A volte, la suddivisione della popolazione in strati dipende dalla differente possibilità di elencare in modo completo le unità appartenenti ai differenti strati.

Per facilitare la stima della media della popolazione, è vantaggioso che il numero di individui campionati in ogni strato sia proporzionale alla loro presenza nella popolazione.

Infatti, indicando con

-   il numero di unità dello strato i presenti nella popolazione,

-   il numero di unità dello strato i raccolti con il campione,

 se

 

 la media generale calcolata sull’insieme dei singoli campioni è una stima non distorta di quella della popolazione.

 

Per valutare se effettivamente esiste una stratificazione nella popolazione, è utile applicare l’analisi della varianza su un campione di dati che consideri questa suddivisione. Ad esempio, se in un campione casuale stratificato (stratified random sample) a 3 strati con 10 unità per ognuno, mediante l’ANOVA è stato ottenuto il seguente risultato

 

 

 si può affermare che tendenzialmente la varianza tra strati (103,5) è circa quattro volte quella entro strati (24,0).

Senza la suddivisione in strati, cioè con un simple random sampling, l’errore standard della media delle 30 misure è

 uguale a 0,99 e

 dove 29, 5 è dato da (207 + 649) / (2 + 27).

Con la suddivisione in tre starti, cioè con stratified sampling, l’errore standard della media delle 30 misure

 

 risulta uguale a 0,89 (si utilizza la varianza entro:  649 / 27).

La stratificazione ha ridotto l’errore standard del 10%.

(Questo confronto è in realtà possibile solo se le due medie campionarie dei 30 dati risultano tendenzialmente uguali, cioè la stratificazione ha rispettato le proporzioni presenti nella popolazione).

 

Nel campionamento stratificato, le dimensioni del campione () di ognuno dei  strati possono essere scelte con modalità differenti. Un modo semplice è raccogliere

-  un numero di dati uguale per ogni strato oppure

-  un numero proporzionale a quello di individui in ogni strato della popolazione.

Una analisi più approfondita del problema dimostra che si ottiene una allocazione ottimale delle risorse quando

-   è proporzionale a

 dove

-    è la deviazione standard delle unità campionate nello strato ,

-    è il costo di campionamento per unità nello strato .

 

Questo metodo permette di individuare l’errore standard minore della media generale, per un determinato costo complessivo dell’operazione di campionamento. A parità di risorse, permette di raccogliere in assoluto il campione di dimensioni maggiori.

 

Il campionamento può essere notevolmente più sofisticato di quanto indicato in questa breve presentazione, che è stata limitata ad una elencazione dei metodi più diffusi e più semplici.

Può essere fatto a due stadi  o due livelli (sampling in two stages, sub-sampling), quando prima si effettua il campionamento delle unità maggiori o del primo stadio (primary sampling units) e successivamente quelle del secondo livello (sub-sample, second-stage units, sub-units) entro ogni primo livello.

Può essere fatto anche a più livelli oppure selezionando con una probabilità proporzionale alle dimensioni dell’unità di campionamento primaria. Per questi e per altri metodi, che superano lo scopo della presente trattazione introduttiva, si rinvia a testi specifici.

Infatti non è possibile una presentazione accurata dei metodi di campionamento, che sia generalmente valida: ogni disciplina e ogni settore di ricerca ricorrono a metodi specifici, collegati alle caratteristiche della distribuzione e della variabilità dei dati.