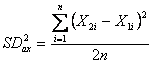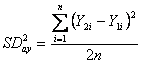LA REGRESSIONE LINEARE MODELLO II  E LEAST-PRODUCTS.

IL CONFRONTO TRA DUE METODI QUANTITATIVI.

 

 

 

24.4.  LA REGRESSIONE MODELLO II O LEAST-PRODUCTS DI DEMING, PER IL CONFRONTO TRA DUE METODI ANALITICI.

 

 

Quando si confrontano i risultati delle determinazioni quantitative di due metodi differenti,

-  gli errori di misura sono uguali, sia per la variabile indicata con , sia per quella con .

 

 

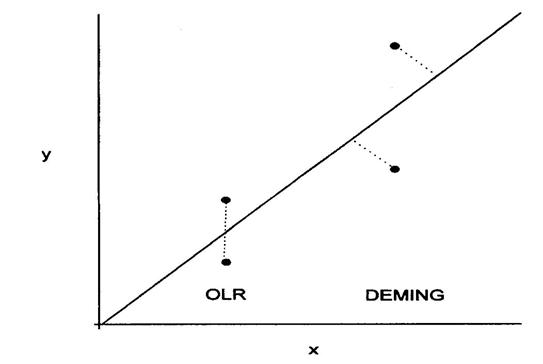
Diagramma di dispersione dei punti ottenuti con due metodi analitici,

analizzati con il metodo dei minimi quadrati e il metodo di Deming

 

La retta di regressione classica,

-  chiamata Ordinary Least-Squares Regression (abbreviata in OLR oppure in LSR)

-  e fondata sul quadrato degli errori della sola variabile Y, non è più adeguata.

 

Già nell’anno 1943, W. E. Deming nel volume Statistical Adjustement of Data (John Wiley and Sons, New York, NY) suggerisce una alternativa statistica tecnicamente corretta, per calcolare la relazione lineare esistente tra i due metodi di misurazione. Essa

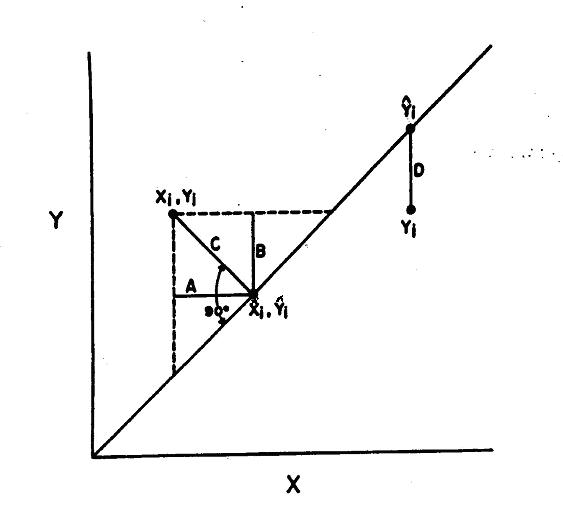
-   è fondata sul principio dei minimi quadrati della distanza perpendicolare alla retta, data dal prodotto (least-products) della distanza simultanea lungo l’asse della variabile  e l’asse della variabile  (minimizing the sum of the squares of the residuals in both the  and   directions simultaneously).

La retta di Deming o least-products è quella che

-  rende minima la somma dei quadrati delle distanze perpendicolari tra i punti e la retta (come illustrato nella figura precedente e, in modo più dettagliato, in quella successiva).

Modello di regressione di Deming (a sinistra) e dei minimi quadrati (a destra)

 

La retta di Deming considera la somma dei quadrati dei residui tra il punto e la retta

- sia lungo l’asse delle ascisse  con   ,

- sia lungo l’asse delle ordinate  con   ,

 e minimizza la distanza   .

 

Il suo coefficiente angolare  su molte riviste di statistica applicata è indicato con

.

 mentre quello least-squares è indicato spesso con

 

Trascurata per diversi decenni, questa metodologia statistica è oggi proposta in molti programmi informatici, scritti appositamente per le analisi cliniche e chimiche. Sulle riviste di biologia e ecologia è chiamata Model II Regression, alternativa corretta alla Model I Regression, discussa nei capitoli precedenti.

Tuttavia questa classificazione dicotomica, diffusa da Robert R. Sokal  e F. James Rohlf già nel 1969 nella prima edizione del loro testo Biometry. The principles and practice of statistics in biological research (3^rd ed. W. H. Freeman and Company, New York,  XIX, + 887 p.) e confermata nelle due edizioni successive del 1981 e del 1995, è criticata in quanto appare poco utile alla esatta comprensione delle differenze tra due metodi di regressione. E’ quanto sostiene, ad esempio, anche Brian H. McArdle nell’articolo del 2003 Lines, models, and errors: Regression in the field (pubblicato sulla rivista della The American Society of Limnology and Oceanography,  Limnol. Oceanogr. Vol. 48 ( 3), pp.: 1363 - 1366). Egli dichiara di preferire la classificazione in

-  metodi con relazioni asimmetriche (asymmetric relationships) tra le due variabili, come la least-squares regression,

-  metodi con relazioni simmetriche (symmetric relationships) tra le due variabili, come la least-products regression.

 

Una presentazione dettagliata del metodo di Deming è stata effettuata da P. Joanne Cornbleet e Nathan Gochman nell’articolo del 1979 Incorrect Least-Squares Regression Coefficients in Method-Comparison Analysis (pubblicato su Clinical Chemistry, Vol. 25, No. 3, pp.: 432-438).

La loro pubblicazione comprende il confronto con il metodo di Mandel (illustrato nella pagine successive) e quello non parametrico di Bartlett (presentato nel capitolo della regressione lineare non parametrica).

 

Per questo articolo, Cornblett e Gochman sono indicati come coloro che hanno avuto il merito di portare il metodo di Deming all’attenzione definitiva della collettività scientifica, che finalmente in larga parte lo considera

- l’alternativa corretta all’impostazione classica, nel caso del confronto tra due metodi di misurazione.

Da questo articolo sono ripresi alcune figure e molti concetti di questo paragrafo.

 

L’analisi della regressione di Deming non attribuisce pesi differenti ai valori (the unweighted form of Deming regression analysis) e

-  è appropriata quando l’errore analitico è costante.

In altri termini, è da ritenere corretta quando la deviazione standard è indipendente dalle dimensioni delle misure.

Quando invece

-  l’errore è costante come percentuale del valore  oppure come coefficiente di variazione rispetto al valore (i due concetti sono analoghi),

 è opportuno utilizzare una delle modifiche successive. Alcune di esse, le più diffuse nella ricerca applicata e più frequentemente citate nelle riviste di analisi cliniche e chimiche, sono presentate nei paragrafi successivi.

 

Le condizioni di validità della retta di Deming, con una formulazione matematica più appropriata, affermano che

-  il valore osservato  è

-  il valore osservato  è

  con .

Le assunzioni su questi errori random sono quattro:

1 -    e   sono entrambi distribuiti in modo normale e con media zero;

2 -  le coppie  e   sono distribuite in modo indipendente per : le covarianze entro metodi (within-method covarainces) sono uguali a zero;

3 -  le coppie  sono distribuite in modo indipendente per ogni : la covarianza tra metodi (between-method covariance) è uguale a zero;

4 -  le varianze  e  non sono costanti, ma è costante il loro rapporto

 

Con  coppie di misure, ottenute con i due metodi   e  che si intende confrontare, per ricavare la retta di Deming, come al solito si devono prima calcolare

- la Devianza delle :

 

-  la Devianza delle :

 

- la Codevianza :

 

-  e dalle due devianze il loro rapporto

 

Da queste, si ricava il coefficiente angolare

 

 

 e con esso l’intercetta  mediante le medie:

La retta di regressione di Deming  è

 

L’errore standard dell’intercetta  e del coefficiente angolare  sono stimate con la procedura Jackknife (alla quale si rimanda, per la presentazione del metodo).

 

In alcuni esperimenti, i valori di  e di  per lo stesso campione misurando sono ripetute due volte. In questo caso, nelle formule precedenti,

-  il valore  è la  media delle due repliche

-  il valore  è la  media delle due repliche

 

Le deviazioni standard analitiche (analitical standard deviations) dei metodi   e  possono essere calcolate rapidamente come differenza tra le due misure:

 

 e

 

 mentre il coefficiente  diventa

 

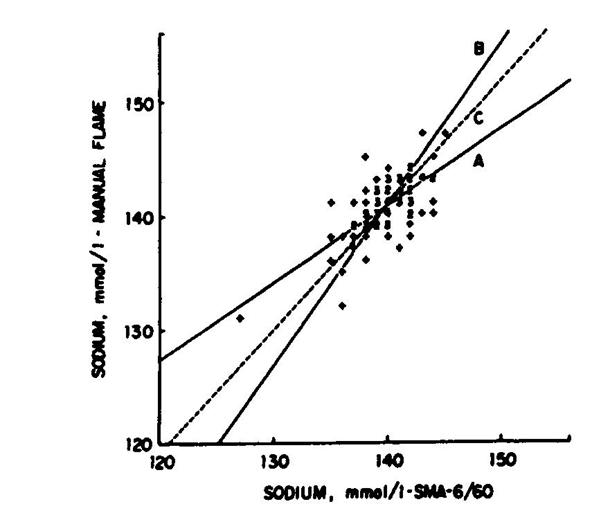
ESEMPIO. (LE DUE RETTE LEAST-SQUARES E LA RETTA LEAST-PRODUCTS DI DEMING, con  PICCOLO). Il numero di dati abitualmente raccolti in queste analisi e la lunghezza dei calcoli richiedono l’uso di programmi informatici. Pertanto, dopo aver presentato il metodo nei suoi passaggi logici, è utile un esempio che illustri i risultati.

Tratta dall’articolo di Cornbleet e Gochman, la figura della pagina successiva mostra il plot di 87 determinazioni di sodio (mmol/L), ottenuti con due metodi flame-photometric:

 

-  il metodo di riferimento, riportato sull’asse delle ,

ha media  = 139,8  e deviazione standard  = 2,67

 

-  il metodo da testare, riportato sull’asse delle ,

ha media  = 140,7  e deviazione standard  = 2,60

 

 

 

 

 

 

Benché la logica indichi che

-  il coefficiente angolare della retta di regressione dovrebbe essere  = 1,0

(se fosse vera l’ipotesi nulla che i due metodi sono equivalenti)

- la regressione least-squares fornisce  = 0,66.

 

Se si scambiano le due variabili  e ,  rendendo  la variabile indipendente,

- la regressione least-squares fornisce la stima  = 1,43.

 

La retta di Deming fornisce la stima  = 1,09.

Essa quindi appare una stima nettamente migliore, rispetto alle due precedenti, della relazione tra   e   che viene stimata dai dati.

 

La sua significatività può essere verificata con vari metodi, tra cui principalmente

-   il test di Bland-Altman (già illustrato in un paragrafo precedente)

-   il test di Passing-Bablok (illustrato in un paragrafo successivo).