LA REGRESSIONE LINEARE MODELLO II  E LEAST-PRODUCTS.

IL CONFRONTO TRA DUE METODI QUANTITATIVI.

 

 

  

24.5.  EFFETTI DEGLI OUTLIER SULLA RETTA LEAST-SQUARES E INDICAZIONI OPERATIVE PER IL CALCOLO DELLA RETTA DI CONFRONTO TRA DUE METODI ANALITICI.

 

 

L’individuazione degli outlier nella statistica bivariata richiede metodi specifici che sono già stati descritti separatamente.

La loro presenza determina problemi non trascurabili, quando si deve calcolare la retta di regressione. Quindi sono stati presentati metodi che permettono di identificarli con facilità, quando si richiede una stima più precisa della retta che deve descrivere la relazione vera tra due metodi di misura.

 

Nel 1966 N. R. Draper e H. Smith nel volume Applied Regression Analysis (John Wiley and Sons, New York, NY, pp.: 44-103) suggeriscono:

- i punti che generano residui maggiori di

- possono essere eliminati nell’analisi della regressione least-squares.

L’analisi dei residui intorno alla retta di regressione può essere un criterio

-  per individuare e successivamente eliminare i dati spuri

-  e quindi annullare i loro effetti sul coefficiente angolare della retta least-squares,

  che in tal modo, con  e  , diventa utilizzabile anche nel confronto tra metodi.

 

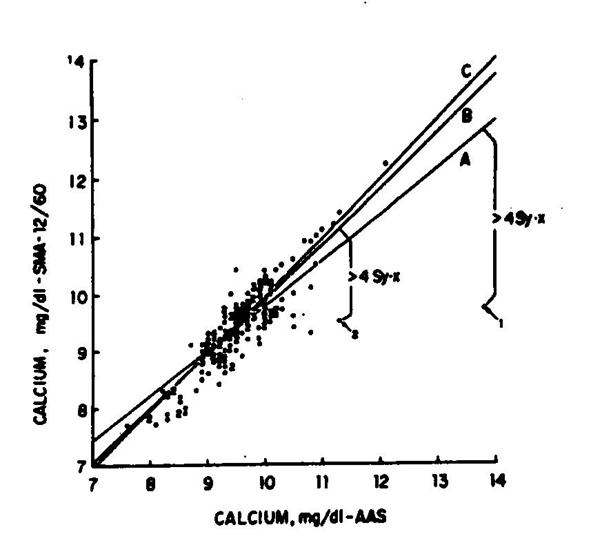
ESEMPIO (ELIMINAZIONE DI DATI SPURI NELLA RETTA LEAST-SQUARES). La Figura riportata nella pagina successiva è il plot di 169 campioni, sui quali è stata fatta  la determinazione (mg/dl) del calcio con due metodi differenti

- per assorbimento atomico  o AAS (asse ),

- e per SMA 12-60 (asse ).

 

Si tratta del confronto tra due metodi.

Perché essi possano essere considerati intercambiabili (ipotesi nulla), la retta dovrebbe avere:

-  intercetta  = 0,0

-  coefficiente angolare  = 1,0.

 

Utilizzando tutti i punti (nel grafico il numero appare minore di 169 in quanto molti sono sovrapposti), si  calcola la retta  di Regressione Least-Squares, con  come variabile indipendente e indicata nel grafico con A:

Essa ha  un valore  = 1,96  e un valore  = 0,78 che sono lontani dall’atteso.

Inoltre, e ciò può essere la causa dello scostamento dall’atteso, il punto indicato con 1 risulta anomalo rispetto alla retta, in quanto

- dista più di  dal punto corrispondente sulla retta.

 

E’ quindi possibile e conveniente

-  eliminare la coppia di dati corrispondente a questo punto

-  e calcolare una nuova retta Least-Squares (con  = 168), ottenendo

Questa seconda retta Least-Squares, indicata con B  è sensibilmente più vicino all’atteso.

Ma essa evidenzia un altro punto che ora è diventato spurio rispetto ad essa.

 

Eliminando i due dati corrispondenti a questo punto 2 (con  = 167),

-  si calcola una nuova retta Least Squares, ottenendo

E’ la retta indicata con C, che non evidenzia più valori spuri, in quanto nessun punto dista più di  dal punto verticale sulla retta.

 

 

 

Con un valore dell'intercetta  molto vicino a 0 e un coefficiente angolare prossimo a 1,

-  può essere una buona stima della relazione lineare attesa tra i due metodi.

 

Nell’articolo di P. Joanne Cornbleet e Nathan Gochman del 1979 Incorrect Least-Squares Regression Coefficients in Method-Comparison Analysis (pubblicato su Clinical Chemistry, Vol. 25, No. 3, pp.: 432-438) la presentazione del metodo di Deming e la dimostrazione degli effetti degli outliers sulla regressione lineare si concludono (a pag. 437) con quattro gruppi di indicazioni operative (guidelines for linear regression analysis).

 

1 - Fare sempre il diagramma di dispersione (plot) dei dati e applicare l’analisi della regressione least-squares solamente nella regione di linearità. Nel grafico, i valori sospettati di essere outlier risultano sempre con evidenza maggiore di quanto possa apparire alla lettura dei valori.

 

2 –  E’ sempre importante stimare l’errore nelle misure. Per un calcolo rapido, è sufficiente

il rapporto

 dove

 -   rappresenta la precisione di una singola misura  vicino alla media .

Se questo rapporto eccede 0,2 si deve dedurre che

- nella stima del coefficiente angolare  ottenuto con i minimi quadrati è presente un errore significativo

- e quindi è più appropriato impiegare il coefficiente angolare  della retta di Deming.

 

Sempre nel dibattito sulla correttezza della regressione least-squares, quando i dati sono marcatamente asimmetrici, come indica il fatto che

-  la deviazione standard delle  () sia maggiore della media  

-  e l'errore nelle misure è proporzionale al valore di ,

 un rapporto uguale o maggiore di 0,15 indica che

-  il coefficiente angolare  della retta least-squares  ha un errore significativo.

 

 3 - Il calcolo del coefficiente angolare  della retta di Deming

 richiede che sia calcolato il rapporto

 

Queste stime possono essere ottenute,

- sia dalla precisione dell’analisi di un singolo campione che sia vicino alla media dei dati,

- sia, quando si dispone di due repliche per ogni campione,

 con

 

Se, per calcolare la retta di regressione, invece dei singoli valori delle due repliche( e  ) ottenute dallo stesso campione, si vuole impiegare solamente la media (), è utile ricordare che

- la deviazione standard della misura medi  è uguale alla deviazione standard calcolata sui singoli valori divisa per .

 

4 – E’ sempre necessario calcolare l’errore standard della regressione ..

Sia per la retta il coefficiente angolare  least-squares, sia per quello last-products di Deming, questa statistica può essere ricavata dalle statistiche abitualmente calcolate su dati bivariati,

con

 

L’errore standard della regressione  deve essere interpretata come l’errore standard del valore medio atteso di  per un dato valore di , collocato vicino alla media .

E’ una misura della dispersione dei punti intorno alla retta di regressione.