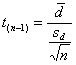LA REGRESSIONE LINEARE MODELLO II  E LEAST-PRODUCTS.

IL CONFRONTO TRA DUE METODI QUANTITATIVI.

 

 

 

24.8.   DIBATTITO SUL CONFRONTO TRA DUE METODI DI ANALISI CLINICHE ED ESEMPI  DI TEST

 

 

Prima della presentazione del test di Bland-Altman, del rilancio della regressione lineare last-products di Deming e della proposta di Passing-Bablok, che in letteratura avvengono all’inizio degli anni ’80 e nella ricerca applicata si diffondono circa 10 anni dopo, il confronto tra metodi presentava una serie di incongruenze tecniche. Erano applicati molti test, ognuno dei quali analizzava solo un aspetto e spesso in modo parziale o non congruo.

L’articolo di  James O. Westgard e Marian R. Hunt del 1973 Use and Interpretation of Common Statistical Test in Method-Comparison Studies (su Clinical Chemistry Vol. 19, No. 1 pp.: 49 – 57) e quelli in cui Bland-Altman e Passing-Bablok presentano i loro metodi denunciano

-  i limiti delle numerose statistiche classiche, quando esse sono applicate al caso specifico del confronto tra due metodi di misura, per valutarne la precisione e l’accuratezza.

 

1 – Il test  di Student per due campioni dipendenti è applicato alle coppie di valori   e  per valutare se esiste una differenza tra le medie dei due metodi.

Se il test risulta significativo, i due metodi non sono giudicati equivalenti, a meno che gli errori casuali non siano molto piccoli. Tuttavia, quando il test non risulta significativo e in particolare quando il valore di  è vicino a 0, occorre ricordare che si possono avere due medie uguali, anche se le singole differenze nelle coppie di misure   e  sono grandissime.

Come evidenzia la formula del test  di Student per due campioni dipendenti

 

i parametri utilizzati forniscono informazioni

-  sulla grandezza relativa dell’errore sistematico (= media delle differenze tra coppie di misure) rispetto all’errore random dei termini ().

Ma la vera informazione importante e necessaria all’analisi di equivalenza tra i due metodi deriva dalle singole differenze (), non dalla loro media.

Infine, utilizzando il test  sarebbe importante conoscere sia , sia , non semplicemente il valore  ottenuto.

 

2 – Il test T di Wilcoxon ha le stesse finalità e la stessa grave incongruenza logica. E’ utilizzato in sostituzione del  di Student, quando la distribuzione delle differenze tra coppie di misure non è normale. E’ riportato insieme con il test , quando la non normalità è solamente sospettata. Oltre ai limiti del t, il test di Wilcoxon  presenta anche quello di non utilizzare né la media delle differenze né la misura della loro variabilità e quindi fornisce una quantità di informazioni ancora minore.

 

3 – Il coefficiente di correlazione  di Pearson tra le  coppie di valori   e  , per misurare il loro grado di accordo lineare (linear agreement), ha indubbiamente la capacità di valutare se le misure campionarie aumentano o diminuiscono insieme. Ma, per verificare l’equivalenza tra due metodi, presenta almeno tre limiti:

 a)  il coefficiente  può essere molto vicino a 1 o addirittura uguale a 1, anche se tra i due metodi esiste un rilevante errore sistematico, come possono essere (ad esempio, con + 12) coppie di valori 1 e 13, 2 e 14, 3 e 15, ecc. … ;

 b)  la dimensione del coefficiente  è influenzato dal campo di variazione delle misure, per cui tende a essere piccolo se i campioni analizzati hanno una distanza ridotta tra il valore minimo e quello massimo; inoltre, non fornisce informazioni sulle dimensioni delle differenze tra coppie di misure;

 c)  il test per la correlazione verifica l’ipotesi nulla  = 0, mentre in questo caso è applicato per valutare l’ipotesi se  è vicino 1 e, idealmente, se è   = 1 (ma in pratica non lo raggiunge mai).

 

4 – I coefficienti di correlazione non parametrici  di Spearman e  di Kendall hanno gli stessi limiti del coefficiente parametrico  di Pearson, ma con il vantaggio di non essere influenzati ugualmente  influenzati dalla presenza di valori anomali.

 

5 – Il test  ottenuto dal rapporto

 

 tra la varianza maggiore e quella minore, calcolate indipendentemente nelle due serie di misure  e   (ma ora quasi tutti i programmi informatici adoperano il test di Levene, più potente) valuta se esiste una precisione (variabilità) differente tra i due metodi; ma come il test  sulle differenze, questo rapporto confronta il livello complessivo di errore nei due diversi metodi e non è un indicatore dell’accettabilità dell’errore tra e entro ognuna delle due serie di misure.

 

Rispetto a tutti questi test statistici, con il vantaggio ulteriore di essere semplice da costruire e da capire (simple both to do and to interpret), il test di Bland-Altman ha il pregio di essere finalizzato esplicitamente alla verifica se due tecniche di misura sono comparabili.

In un loro articolo divulgativo del 1986 (J. M. Bland e D. G. Altman, Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement, pubblicato su The Lancet, February 8, 1986, pp.: 307-310) presentano il problema con la domanda: Do the two methods of measurement agree sufficently closely?

Resta da comprendere cosa si intenda con il termine metodi comparabili e quale sia la definizione di differenze accettabili tra i due metodi. La risposta non deve provenire dal tecnico che effettua le misure, ma dall’esperto della disciplina che se ne serve. Ad esempio, nelle analisi cliniche potrebbe significare che la diagnosi e la prescrizione non cambiano, se l’analisi biologica effettuata al paziente è stata condotta in laboratorio con un metodo oppure con un altro.

 

 

 

Per presentare e interpretare in modo corretto il plot di Bland-Altman, è utile seguire le indicazioni di

-  Katy Dewitte et alii nell’articolo del 2002  Application of the Bland-Altman Plot for Interpretation of Method-Comparison Studies: A Critical Investigation of Its Practice (su Clinical Chemistry Vol. 48, No. 5, pp.: 799 - 801) e commentate da

-  Douglas G. Altman e J. Martin Bland in Commentary on Quantifying Agreement between Two Methods of Measurement (su Clinical Chemistry Vol. 48, No. 5, pp.: 801 - 802).

 

Riportando

-  sull’asse delle ascisse la media dei risultati dei due metodi  sullo stesso campione

-  sull’asse delle ordinate la differenza in valore assoluto dei risultati dei due metodi  sullo stesso campione

 è diffuso come sostituto dell’analisi della regressione lineare.

 

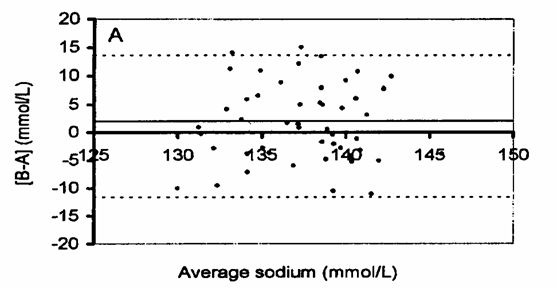
Come nella precedente figura A, quando le analisi cliniche utilizzano concentrazioni che variano in un campo limitato e per valori proporzionalmente vicini (nell’esempio, hanno valori medi da 125 a 150), le differenze si mantengono costanti. E’ quindi corretta la loro rappresentazione e analisi mediante i valori assoluti. La media delle differenze (linea continua più sottile) e i limiti  (le due linee tratteggiate, a distanza simmetrica dalla media) descrivono correttamente la distribuzione delle differenze.

 

 

 

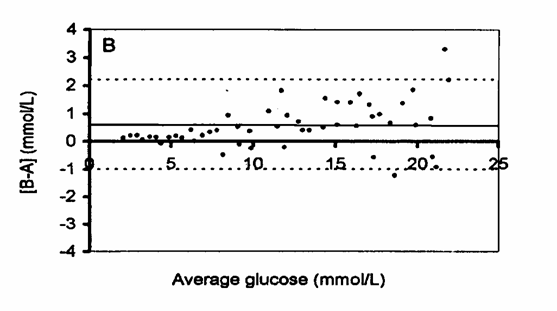
Ma in molte situazioni sperimentali, la deviazione standard delle misure aumenta con la concentrazione e quindi anche le differenze tra i due metodi.

Nella figura B, i valori medi (asse delle ascisse) presentano una estensione molto grande: variano approssimativamente da 2 a 22. Le differenze in valore assoluto (asse delle ordinate) indicano una crescita proporzionale. Esse non sono descritte in modo corretto

-  né dalla media (le prime differenze sono inferiori e le ultime sono prevalentemente superiori)

-  né tanto meno dai limiti  (le prime differenze sono piccole, le ultime sono grandi).

 

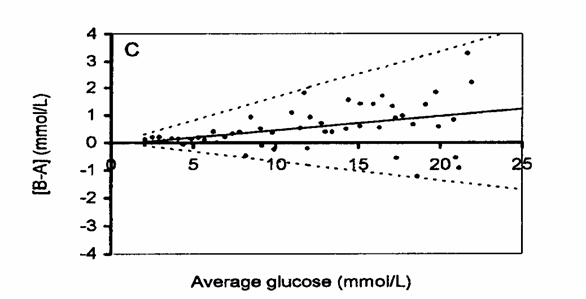
Una loro descrizione corretta è fornita dalla figura C, nella quale la media delle differenze in valore assoluto(linea continua più sottile) e l’intervallo di confidenza  (linee tratteggiate) indicano la quantità effettiva di variazione all’aumentare della concentrazione. Tuttavia è preferibile non utilizzare questa rappresentazione delle differenze assolute, ma ritornare a una grafico con una media e a un intervallo  costanti, mediante la trasformazione delle differenze.

Ma quale trasformazione è migliore?

 

Quando la deviazione standard  aumenta con la concentrazione,

-  Bland e Altman hanno raccomandato di riportare sulle ordinate il logaritmo delle differenze

-  altri propongono la loro trasformazione in percentuale,

 come M. A. Pollock e alii nell’articolo del 1992 Method comparison – A different approach (su Annals of Clinical Biochemistry  Vol. 26, pp.: 556 - 560) e Katy Dewitte nell’articolo citato del 2002.

 

 

 

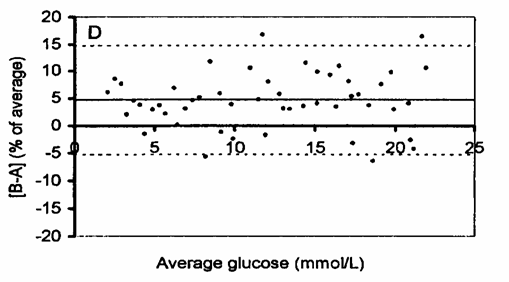
Nella figura D è riportata la rappresentazione corretta, che usa la trasformazione in percentuale

Benché generalmente non vi sia molta differenza nei risultati grafici tra la trasformazione logaritmica e quella in percentuale, è preferibile il plot della percentuale, eccetto quando le concentrazioni si estendono su un campo di rilevazioni molto ampio, che varia di diversi ordini di grandezza:

-   i numeri possono esser letti direttamente sul plot, senza richiedere una retro-trasformazione,

-  il plot include sia la linea della media delle differenze, sia le due linee dei limiti () sperimentali osservati.

 

Nel test di Bland-Altman la significatività non è fornita da calcoli statistici, ma consiste essenzialmente nel confronto (effettuato da un esperto della disciplina) dei due limiti () con la differenza clinicamente accettabile tra due metodi.

Tuttavia, su molte riviste, in aggiunta al metodo di Bland-Altman, sono riportate

-   l’analisi della correlazione,

-   l’analisi della regressione,

-  il test sulla concordanza (K di Cohen).

 con la motivazione che il plot delle differenze è complementare, non sostitutivo.

E’ di questa opinione anche il National Committee for Clinical Laboratory Standard, secondo le linee guida del 1995, pubblicate nel manuale Method comparison and bias estimation using patient samples, approved guideline (NCCLS publication EP9-A, Villanova, PA:NCCLS,1995).

Esso raccomanda di

-  costruire il diagramma di dispersione dei dati  e ,

-  calcolare e riportare nel diagramma la retta di regressione (Deming o Passing-Bablok),

-  analizzare con ottica disciplinare il plot delle differenze di Bland-Altman.

 

Un aspetto importante nell’analisi della equivalenza tra due metodi è l’utilizzazione di misure ripetute, che secondo Bland e Altman sarebbero sempre necessarie, per meglio capire le diverse origine degli errori. Come nell’analisi della varianza a due criteri, nel calcolo della differenza reale tra i due metodi permetterebbe di eliminare gli effetti di altri fattori ambientali (come le differenze tra operatori, tra strumenti, ecc.), che per un confronto corretto dovrebbero essere uguali. In questo caso, la retta di regressione e l’analisi di Bland-Altman si avvalgono solo delle due variabili quantitative.

A favore delle misure ripetute,  Douglas G. Altman e J. Martin Bland nella discussione del 2002 in Commentary on Quantifying Agreement between Two Methods of Measurement (su Clinical Chemistry Vol. 48, No. 5, pp.: 801 - 802) scrivono:

- Another important issue is that the full comparison of the performance of two methods of measurement ougth to include repeated measurements. Such repeat data can be used to compare observers or instruments, or simply to assess random error.

Ma è un metodo impiegato raramente. Un esempio, ma al quale è stato applicato il test di Passing-Bablok, è riportato nelle pagine successive.

 

Come indicazione delle modalità di pubblicazione di un test per il confronto tra due metodi con il test di Passing e Bablok e dell’uso della regressione lineare per la calibrazione, è vantaggioso seguire l’articolo di Torsten Arndt e alii del 2004 Total Plasma Homocysteine Measured by Liquid Chromatography-Tandem Mass Spectrometry with Use of 96-Well Plates (su Clinical Chemistry Vol. 50, No. 4, pp.: 755 – 757) dal quale sono tratte anche le due figure seguenti.

 

L’aumento del plasma totale o siero omocisteina è considerato un fattore di rischio per malattie collegate all’occlusione delle arterie o delle vene.

Il problema tecnico da affrontare è che il metodo classico, denominato HPLC, richiede molto tempo e materiale costoso. Dagli autori dell’articolo è quindi proposto un metodo nuovo, denominato sistema LC-MS/MS, che presenta alcuni vantaggi pratici ma del quale deve essere preventivamente dimostrata la comparability, per affermare che può vantaggiosamente sostituire quello precedente.

 

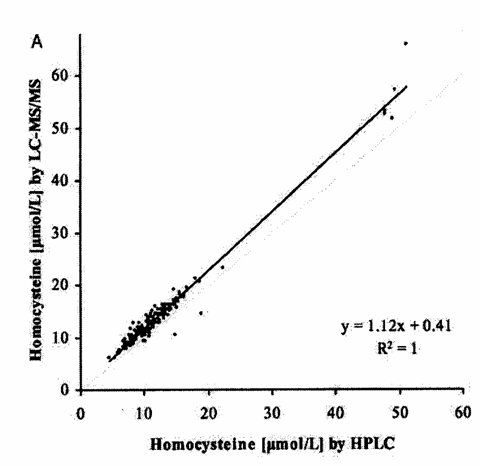
L’analisi è stata condotta su 187 campioni di plasma.

Il diagramma di dispersione, riportato nella figura A successiva, è costruito ponendo

-  sull’asse delle ascisse i valori ottenuti con il metodo vecchio e consolidato, cioè la quantità di omocisteina in  con il metodo HPLC,

- sull’asse delle ordinate i valori ottenuti con il metodo nuovo, cioè la quantità di omocisteina in  con il metodo LC-MS/MS.

 

La funzione di regressione di Passing-Bablok

 è

 espressi in .

 

Per il coefficiente angolare   l’intervallo di confidenza al 95%  è tra 1,075 e 1,162.

Per l’intercetta   l’intervallo di confidenza al 95%  è tra –0,049 e + 0,856

Si può dedurre che

-   mentre è accettabile l’ipotesi  = 0

-  il coefficiente angolare è statisticamente differente da .

 

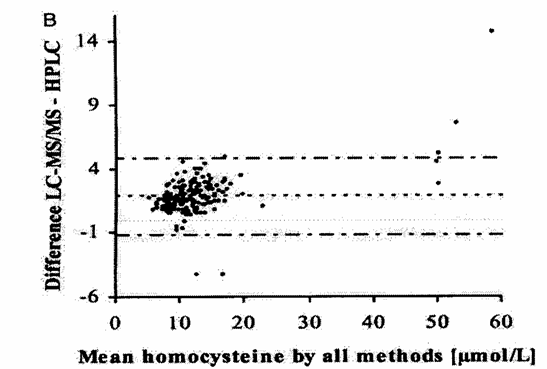
L’analisi di Bland-Altman, riportata nel figura B, mostra che

-   la media delle differenze tra le coppie di valori è 1,81

-   intervallo  è compreso tra circa 5 e circa –1 (la lettura del grafico non permette di essere più precisi).

 

 

 

La conclusione degi autori è che tra i due metodi esistono differenze che sono

-   statisticamente significative,

-  ma trascurabili, l’aspetto biologico o clinico.

Infine, poiché sulla base dei loro esperimenti il metodo nuovo permette un risparmio del 90% per quanto riguarda il materiale e del 60% per quanto riguarda i tempi e quindi i costi del personale rispetto a quello classico, propongono come più vantaggioso l’uso del metodo nuovo.

 

Nell’articolo del 2003 di Markus J. Schwarz  e alii dal titolo Multicentre evaluation of a new assay for determination of carbohydrate-deficient transferrin (su Alcohol & Alcoholism Vol. 38, No.3 pp.: 270 – 275) è riportato un esempio di misure ripetute allo scopo di valutare anche le differenze tra metodi e laboratori. Ma in questo caso è preentata solamente la parte che riguaeda tutti i dati.

Il Carbohydrate-Deficient Transferrin (CDT) è ritenuto un eccellente marcatore biochimico di un consumo eccessivo di alcol. Esiste consenso internazionale che il CDT sia misurato in modo adeguato mediante il metodo High-Performance Liquid Chromatography (HPLC). Recentemente, è stato sviluppato un metodo chiamato Tina-quant%CDT 2^nd generation che viene confrontato con il precedente, mediante l’analisi della regressione di Passing-Bablok.

 

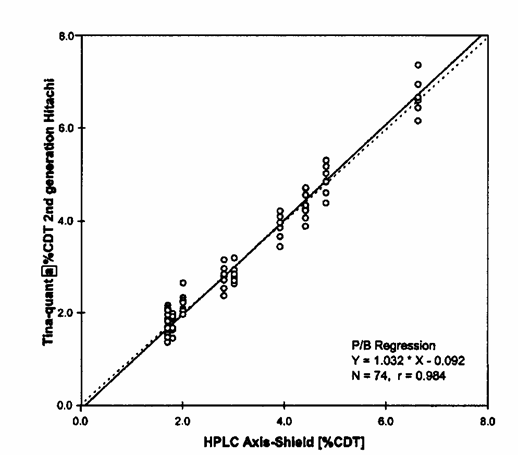
La retta risulta

 e il coefficiente di correlazione è

 

 Sulla base di queste due sole  analisi, gli autori concludono che l’accordo tra i due metodi è molto buono: Very good agreement, with a slope of 1.03, a negligeable intercept of –0,1% CDT and a correlation coefficient () of 0,984, was obtained.

 

 

In molte pubblicazioni, la verifica della comparability non è fondata solamente sul test di Passing- Bablok e sul test di Bland-Altman, ma si serve anche di misure di correlazione  o misure della capacità predittiva , oltre che del test  di Student per la significatività delle differenze tra le due serie di misure appaiate.

Questi ulteriori test sulla corrispondenza tra due metodi analitici in realtà possono condurre in errore coloro che non sono esperti della disciplina. E’ solamente la conoscenza degli effetti biologici o clinici che permette di decidere quando due metodi sono in realtà bioequivalenti e di sapere quale sia il margine di errore accettabile, in quella situazione specifica.

 

Infatti per campioni grandi, e in questi confronti quasi sempre si supera il centinaio di osservazioni, i test tendono a essere significativi, anche quando le differenze sono biologicamente trascurabili.

Dominique Gerbet, Phlippe Richardot e alii  nell’articolo del 1983 New Statistical Approach in Biochemical Method-Comparison Studies by Using Westlake’s Procedure, and Its Application to Continous-Flow, Centrifugal Analysis, and Multilayer Film Analysis Techniques (su Clinical Chemistry Vol. 29, No. 6, pp.: 1131 – 1136) a pag. 1135 scrivono:

- The joint testing procedure provided significant differences () for all pairwise comparisons. The reason is that, when available experimetal data are numerous, variances of   and  are very small. Hence, the smallest deviation from the point (, ) is regarded as statistically significant, even though not significant biologically.

 

Quando le misure fornite dai due metodi di analisi sono di tipo qualitativo binario oppure a più livelli e ordinabili per rango, l’accordo tra i due metodi deve essere stimato e verificato mediante il test K di Cohen (al quale si rimanda).