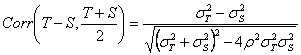LA REGRESSIONE LINEARE MODELLO II  E LEAST-PRODUCTS.

IL CONFRONTO TRA DUE METODI QUANTITATIVI.

 

 

 

 

24.9    IL CONFRONTO CON IL GOLD STANDARD: UTILIZZARE IL METODO DELLA CALIBRATION OPPURE QUELLO DELLA COMPARABILITY?

 

 

Per valutare l’accordo (agreement) tra due serie di misure, determinate con metodi differenti, è possibile impiegare

-  sia le tecniche di calibration (già illustrate nel capitolo sulla regressione lineare),

-  sia i metodi di comparability (illustrati in questo capitolo).

 

Si ricorre alla comparability, quando entrambi i metodi hanno la stessa quantità di errore (reproducibility). Nessuno dei due è più preciso dell’altro.

 

Si ricorre alla calibration, quando un metodo è preciso e l’altro presenta una variabilità (deviazione standard) elevata. Il caso classico di calibration è rappresentato dalla relazione tra la dose di un farmaco ( nota con precisione) e la risposta biologica ( con variabilità o errore) indotta sul paziente.

 

Quando per effettuare la stessa analisi esistono almeno due metodi, spesso avviene che

-  un metodo (chiamato C, da crude) di norma sia più economico, ma meno preciso, mentre

-  l’altro (chiamato P, da precise) sia costoso (in denaro o tempo richiesto), ma molto preciso.

Considerazioni di convenienza economica e di praticità,

-  rendono il metodo meno preciso () più attraente di quello più preciso ()

-  e quindi spingono a utilizzare il primo () per stimare i valori del secondo metodo ().

Ma prima deve esserne dimostrata l’equivalenza.

Con quale metodo?

 

Con la calibrazione si stima il valore del metodo precise, partendo dal valore del metodo crude, più facilmente disponibile.

Il calcolo avviene con due passaggi:

1 -  dalla variabile precise (), in cui la X ha un errore piccolo, si ricava la variabile Y crude () attraverso la retta di regressione least-squares:

 

2 – dalla stima della variabile crude Y (), si ricava il valore della variabile precise X (), con il percorso inverso, ma sempre

 con la regressione least-squares

 che invertita diventa

 

Soprattutto nel caso del confronto tra un metodo nuovo e un gold-standard, da molti studiosi di statistica sono ritenuti corretti la regressione least-squares e la calibration. Ad esempio, Alan M. Batterman nell’articolo del 2004 Commentary on Bias in Bland-Altman but not RegressionValidity Analyses (su Sportscience Vol. 8 pp.: 47-49) afferma che  le tecniche classiche di regressione least-squares possono essere impiegate correttamente:

-   per la calibratura, quindi per la conversione da un metodo all’altro;

-  negli studi di validità di un metodo, particolarmente nelle situazioni in cui il test di confronto è conosciuto o è gold-standard;

-  infine, quando l’errore di misura della X e della Y è piccolo, rispetto al campo di variazione dei dati e al loro effetto biologico.

 

Altri contestano questa scelta e suggeriscono ugualmente l’uso del plot di Bland-Altman.

In particolare J. Martin Bland e Douglas G. Altman, che nel 1995 in Comparing methods of measurement: why plotting differences against standard method is misleading (su Lancet Vol. 346, pp.: 1085-1087) sostengono come anche in questo caso sia corretto solamente utilizzare il loro metodo, soprattutto nel confronto tra misure cliniche, in cui la equivalenza tra i metodi dipende in larga parte dall’esperienza dello specialista.

Quando si confrontano due metodi e uno dei due è considerato lo standard,

-   è fuorviante il concetto che tale termine sia sinonimo di misura vera o corretta;

-  inoltre, la situazione non è differente quando il metodo di riferimento è definito gold standard.

 

Le conseguenze statistiche che il gold-standard possa rappresentare la misura di riferimento senza errore sono state analizzate in profondità da Bland e Altman. Accettando tale idea, sull’asse delle ascisse dovrebbe essere riportato il valore dello standard, non più la media dei due metodi.

Ma a pag. 1085 essi scrivono:   it is sometimes argued that when one method may be regarded as a “gold standard”, it is presumably more accurate than the other method and so we should plot the difference against the gold standard. We think that this idea is misguided and is likely to lead to misinterpretation. Here we will show why, and that the plot of difference against average is almost always preferable.

 

La dimostrazione tecnica di tale affermazione è fondata sulla stima della correlazione tra le differenze e le medie delle coppie di valori, rilevati con i due metodi a confronto.

Indichiamo

-  con  il metodo da testare e con  lo standard,

-  con  il coefficiente di correlazione tra le due serie di misure,

-  con   e   le varianze rispettivamente della serie di valori  e .

 

Quando l’analisi di due metodi include un campo di variazione dei valori che sia grande e le due varianze    e   sono simili, il coefficiente di correlazione tra le coppie di misure di solito risulta alto (), a meno che l’accordo (agreement) tra i due metodi sia estremamente basso.

 

Allorché i risultati sono rappresentati nel plot di Bland-Altman,

tra la differenza  e la media  si ha una correlazione apparente

 che è

 

Come evidenzia questa formula, la correlazione tra la differenza  e la media

-   è zero, se le due varianze sono uguali;

-   è sempre piccolo, eccetto quando esiste una differenza grande tra le due varianze.

 

Se il plot venisse costruito in modo diverso, collocando sull’asse delle ascisse il valore dello standard, si avrebbe che la correlazione tra la differenza  e il valore dello standard

è

 

Di norma, questa correlazione risulta negativa (poiché  e   = ).

Ne consegue che, quando le due varianze sono uguali e inoltre non esiste correlazione tra le differenze e la grandezza dei valori,

-  il plot delle differenze, che sull’asse delle ascisse abbia riportato i valori dello standard, mostra una correlazione  che tende alla quantità

Questa correlazione spuria è piccola, quando i due metodi sono altamente correlati (quindi  tra le coppie di osservazioni).

Si ha il fenomeno opposto, allorquando sull’asse delle ascisse è riportato il valore del metodo . Si determina sempre una correlazione spuria della stessa quantità, ma di segno positivo.

I concetti sono illustrati con una serie di esempi, tratti dall’articolo di J. Martin Bland e Douglas G. Altman del 1995, già citato.

 

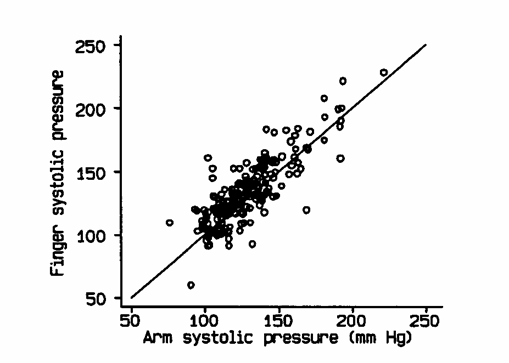
Figura 1. Diagramma di dispersione con il valore della misura standard () al braccio e il valore al dito ().   La linea continua rappresenta la retta teorica della uguaglianza ( = 0  e  = 1).

 

 

Il metodo classico o standard per determinare la pressione sistolica (mm Hg) di un individuo è la misura presa al braccio. Un metodo alternativo o test, del quale si vuole analizzare la corrispondenza, è la pressione al dito: We saw the aim of such studies as to determine wheter two methods agreed sufficiently well for them to be used interchangeably.

 

A questo scopo sono state prelevate le misure su

-   un campione abbastanza numeroso di 200 pazienti,

-  che presentano una variabilità grande.

 

Infatti nella figura 1 è possibile osservare che i livelli minori hanno approssimativamente valore 100 e quelli maggiori valori prossimi a 200, anche escludendo le osservazioni più estreme.

La rappresentazione grafica classica (Figura 1), vale a dire il diagramma di dispersione nel quale

-  sull’asse delle ascisse è riportato il metodo standard

-  sull’asse delle ordinate il metodo nuovo,

si dimostra inefficiente, poiché

-  i punti tendono a essere aggregati lungo la linea dell’uguaglianza ( = 0  e   = 1)

 soprattutto se, come atteso in questo caso, i due metodi forniscono misure tra loro collegate.

Il valore del coefficiente di correlazione tra pressione al braccio (standard) e pressione al dito (test) risulta  = 0,87.

 

 

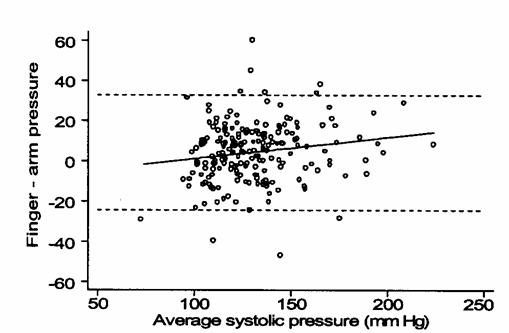
Figura 2. Diagramma di Bland-Altman con la media  dei due metodi () e la differenza tra i due metodi (): test-standard.   La linea continua rappresenta la retta di regressione tra la media delle coppie di valori e la loro differenza. Le linee tratteggiate sono la media delle differenze

 

 

Il plot di Bland-Altman si dimostra più utile del diagramma di dispersione e del calcolo della retta di regressione, per l’analisi dell’equivalenza tra i due metodi.

La media delle differenze (test – standard o dito meno braccio) risulta +4,3 (mm Hg) e la deviazione standard di queste differenze è  = 14,6 (mm Hg). Da questi dati deriva che

-   il limite inferiore è  4,3 – 1,96 x 14,6 = -24 mm Hg

-   il limite superiore è  4,3 + 1,96 x 14,6 = +33 mm Hg

Inoltre nel grafico è riportata

-  la retta di regressione della differenza () sulla media ()

-  e il coefficiente di correlazione tra media e differenza è  = 0,17.

Si evidenzia anche che il dito (test) tende a dare valori più alti del braccio (standard), all’aumentare della pressione.

 

E’ quindi presente un errore sistematico (bias), che in precedenza la retta di regressione, anche nella condizione teorica ( = 0  e  = 1), non riusciva a evidenziare.

 

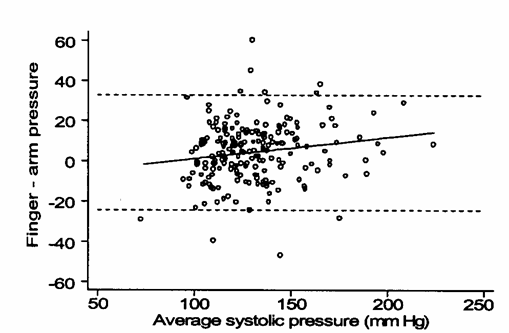
Il confronto del test (metodo nuovo) con il gold-standard non modifica i risultati emersi da questo confronto, per quanto riguarda la retta di regressione e il metodo di Bland-Altman.

Infatti il diagramma delle differenze, costruito non più sui valori medi delle coppie di osservazioni ma sul valore dello standard (Figura 3), ritenuto il valore vero e quindi senza errore, determina in realtà un errore sistematico, rispetto al bias reale precedente, in accordo con la teoria presentata.

 

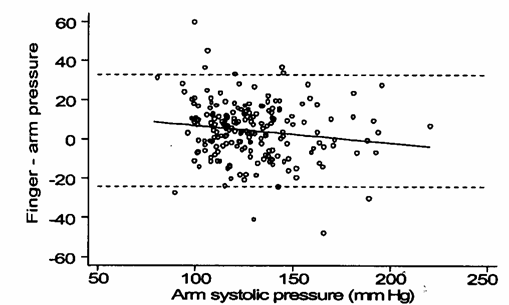
Figura 3. Diagramma di Bland-Altman con il valore dello standard () e la differenza tra i due metodi (): test-standard.   La linea continua rappresenta la retta di regressione tra il valore dello standard e la differenza.  Le linee tratteggiate sono la media delle differenze

 

Nel grafico precedente è riportata

-  la retta di regressione della differenza () sul valore dello standard

-  e il coefficiente di correlazione, che  tra il valore dello standard e la differenza è  = - 0,14.

E’ un valore negativo, come predetto dalla formula, ma per una quantità inferiore

 all’atteso

 che è .

 

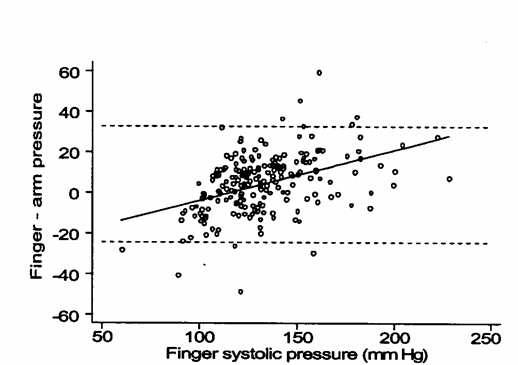
E’ la dimostrazione sperimentale che quando sull’asse delle ascisse viene riportato il valore del test, si ha ugualmente un errore sistematico, ma di segno opposto.

 

Figura 4. Diagramma di Bland-Altman con il valore del test () e la differenza tra i due metodi (): test-standard.   La linea continua rappresenta la retta di regressione tra il valore del test e la differenza.  Le linee tratteggiate sono la media delle differenze

 

 

Nel grafico è riportata

-  la retta di regressione della differenza () sul valore del test

-  e il coefficiente di correlazione, che  tra il valore del test e la differenza è  = + 0,44.

 

Le tre correlazioni (quella del grafico esatto e le due calcolate con il valore dello standard oppure del test riportato sull’asse delle ascisse), risultano tutte significative.

La conclusione di Bland e Altman è che le ultime due forniscono informazioni sbagliate, come dimostrano le formule matematiche e la loro applicazione ai dati sperimentali. Inoltre sono tutte significative e tra loro contraddittorie: Thus we get significant correlations in different directions!

 

Su quale sia la tecnica statistica migliore, in quanto più appropriato e semplice, per confrontare due metodi di misura, Bland e Altman non hanno dubbi: il loro. E’ un concetto che riportano in forme leggermente diverse in molti loro articoli.

Ad esempio, in Statistical methods for assessing agreement between two methods of clinical measurement  (su Lancet 1986; i, pp.: 307-310),

-  nella summary scrivono:

 In clinical measurement comparison of a new measurement technique with an established one is often needed to see whether they agree sufficiently for the new replace the old. Such investigations are often analysed inappropriately, notably by using correlation coefficients. The use of correlation is misleading. An alternative approach, based on graphical techniques and simple calculations, …

- Nella conclusione scrivono

In the analysis of measurement method comparison data, neither the correlation coefficient … nor techniques such as regression analysis are appropriate. We suggest replacing these misleading analyses by a method that is semple both to do and to interpret.