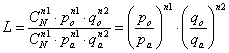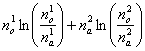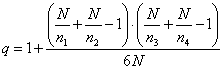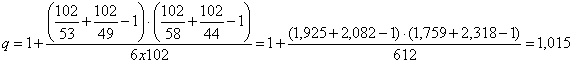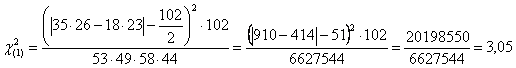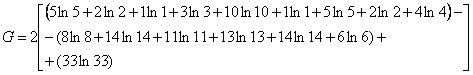|
CAP III - ANALISI DELLE FREQUENZE
3.10. IL LOG-LIKELIHOOD RATIO O METODO G
Il test c2 rappresenta il metodo classico. Più recentemente, vari testi e programmi informatici a grande diffusione hanno riproposto il Log-likelihood ratio o test G, indicato nel passato anche con G2, che utilizza i logaritmi naturali. Rispetto al test c2 questo metodo, che affronta gli stessi problemi inferenziali, ha il vantaggio di richiedere calcoli semplici quando il disegno diventa complesso, come in matrici a più di due dimensioni. Sotto l’aspetto teorico, il vantaggio principale di questo metodo è di essere ritenuto un metodo più “robusto” del c2 e a volte più potente, nel caso di frequenze piccole. Nel 1978 K. Larntz (nell’articolo Small-sample comparisons of exact levels for chi-squared goodness-of-fit statistics, pubblicato su Journal of the American Statistical Association vol. 73, pp. 253-263) ha dimostrato che, quando le frequenze attese variano tra 1,5 e 4, alla significatività del 5% permette di rifiutare l’ipotesi nulla molto più spesso del c2, mentre non ha trovato differenze quando le frequenze attese sono 0 oppure 1. Questi confronti tuttavia non hanno considerato gli effetti delle correzioni proposte nel 1976 da D. A. Williams (con l’articolo Improved likelihood ratio test for complete contigency tables, pubblicato su Biometrika vol. 63, pp. 33-37), che forniscono un risultato più conservativo e che riportano il G a valori più vicini a quello del c2corrispondente.
Il Maximum Likelihood Estimate (MLE) di un parametro è il suo possibile valore, supponendo che esso coincida con quello del campione. Il log likelihood ratio, chiamato in italiano logaritmo del rapporto di verosimiglianza o, con termine meno tecnico, log del rapporto di probabilità, è fondato appunto sul logaritmo naturale o neperiano di tale rapporto. Per comprendere il significato insito nel metodo, è utile rifarsi ad un esempio semplice di confronto tra una distribuzione binomiale osservata ed una distribuzione attesa. Si supponga di avere ottenuto da un esperimento di Mendel, su un totale di 104 individui, 89 con il fenotipo A e 15 con il fenotipo a, mentre l’atteso rapporto di 3 a 1 avrebbe dovuto dare 78 individui A e 26 individui a. Il calcolo del log-likelihood ratio test for goodness of fit si sviluppa nei quattro passaggi logici:
1 – con la distribuzione binomiale, calcolare la probabilità P esatta di trovare 89 individui di tipo A e 15 individui di tipo a, nell’ipotesi che la probabilità p vera di avere un individuo A sia quella sperimentale di 89/104 e, ovviamente, che la probabilità q di avere a sia 15/104:
2 – sempre con la distribuzione binomiale calcolare la probabilità P esatta di trovare 89 individui di tipi A e 15 di tipo a, questa volta nell’ipotesi che la probabilità p vera di avere un individuo A sia quella attesa o teorica di 3/4 e quella di avere un individuo a sia 1/4:
che può essere scritto anche come
3 - la prima probabilità è sempre maggiore della seconda poiché si fonda sui dati osservati; la seconda è tanto più vicina alla prima quanto più l’atteso è vicino al valore osservato; il test è fondato sul rapporto L L = 0.110071 / 0.00337 = 32,85
4 – la distribuzione del valore L è complessa e poco conosciuta; è invece nota la distribuzione G derivata da L, data da G = 2 ln L(dove ln indica il logaritmo naturale). Nel caso di grandi campioni è bene approssimata dalla distribuzione c2 con gli stessi gdl (che in questo esempio è uguale a 1). Con i dati dell’esempio G = 2 ln L = 2 ln 32,85 = 2 x 3,49 = 6,98 G risulta uguale a 6,98; poiché il valore del chi-quadrato alla probabilità 0.05 e per 1 gdl è uguale a 3,84 si conclude che la presenza di individui A è significativamente maggiore dell’atteso.
Spesso al posto di G si usa la simbologia 2I, per specificare che G è il doppio dell’informazione contenuta nel campione: infatti il rapporto L è calcolato mediante l’informazione contenuta sia nel campione sia nell’atteso, cioè sia nell’ipotesi H1 alternativa (il campione) sia nell’ipotesi nulla H0 (l’atteso).
Quanto spiegato nell’esempio svolto contiene anche le informazioni per derivare e comprendere la formula base del test G. Indicando con n1 la frequenza osservata del primo gruppo, n2 la frequenza osservata del secondo gruppo, N il numero totale di osservazioni (N = n1 + n2), po la probabilità osservata del primo gruppo, qo la probabilità osservata del secondo gruppo, pa la probabilità attesa del primo gruppo, qa la probabilità attesa del secondo gruppo, la formula utilizzata può essere scritta
Poiché n1 osservato = Npo e n2 osservato = Nqo e similmente n1 atteso = Npa e n2 atteso = Nqa
da cui ln
L = Per la significatività, il valore di G non ha una sua tabella, ma utilizza la stessa distribuzione dei valori critici del c2 e ha gli stessi gradi di libertà. Il test likelihood ratio può essere applicato nei 3 casi già descritti: a – il confronto tra una distribuzione osservata e la corrispondente distribuzione attesa; b – il confronto tra due campioni indipendenti, in tabelle 2 x 2; c – il confronto tra più campioni indipendenti in tabelle M x N. A questi può essere aggiunto il caso di tabelle a più dimensioni (quando i fattori sono più di 2 ognuno con p modalità), che è molto difficile analizzare con il metodo c2.
3.10.1 Confronto tra una distribuzione osservata ed una attesa con la correzione di Williams Nel caso del confronto tra una distribuzione osservata e la corrispondente distribuzione attesa, il calcolo di G può essere ottenuto con una delle due formule sottoriportate, di cui la prima risulta più rapida per i calcoli manuali G o
likelihood ratio = dove, la sommatoria å è estesa a tutte le k caselle, ln = logaritmo naturale, Oss. = frequenze osservate, Att. = frequenze attese, in accordo con l’ipotesi nulla.
Quando il campione è inferiore alle 200 unità, Williams ha proposto la seguente correzione q
dove k = il numero di gruppi; n = il numero di gradi di libertà; N = il numero totale di osservazioni. Quando il numero di g.d.l. è uguale al numero di gruppi meno 1 (come è nella norma di gruppi tra loro indipendenti) e quindi n = k – 1, la formula può essere semplificata in
Nel caso di due gruppi, la formula può essere scritta come
Il valore di G corretto (adjusted), simboleggiato con Gadj, è ottenuto con il rapporto
ESEMPIO 1. Per valutare la ricchezza in specie di 4 zone (A, B, C, D) sono state contate le specie presenti, con il seguente risultato:
Esiste una differenza significativa tra le 4 zone? Valutare la risposta con il test c2 e con il metodo G, senza e con la correzione.
Risposta. Dopo aver calcolato il totale e la frequenza attesa in ogni classe nella condizione che sia vera l’ipotesi nulla,
si calcola il valore del c2 che ha 3 gdl
e risulta uguale a 9,441; con la correzione di Yates il valore diminuisce a
9,160. Usando il metodo G
si ottiene un valore di 9,450; con la correzione di Williams il valore q, stimato con la formula
dove k = 4 e N = 163
risulta uguale a 1,0051 e quindi il valore di Gadj
risulta uguale a 9,402. In questo esempio, il valore di G risulta leggermente superiore a quello del corrispondente c2. Poiché il valore critico del c2 con 3 gdl alla probabilità 0,05 è uguale a 7,815 è possibile rifiutare l’ipotesi nulla.
ESEMPIO 2. Nell’incrocio tra due ibridi Aa x Aa, sono stati contati 95 individui con fenotipo A e 41 con fenotipo a. E’ una distribuzione in accordo con l’atteso di 3 a 1?
Risposta. Dopo aver calcolato le due frequenze attese
si calcola si valore di G
che risulta uguale a 1,844 da confrontare con quelli riportati nella tabella del c2 con i gdl.
La correzione q di Williams è
uguale a 1,0037 per cui il valore di G aggiustato per le dimensioni non grandi del campione è
uguale a 1,837.
3.10.2 Tabelle 2 x 2, con la correzione di Williams e quella di Mantel-Haenszel. Nel caso di tabelle 2 x 2, per verificare l’indipendenza tra il fattore riportato in riga e quello riportato in colonna, entrambi con variabili binarie, usando la consueta simbologia per le frequenze assolute
il valore di G o Log-likelihood ratio è dato da
Sempre da impiegare nel caso di campioni con meno di 200 osservazioni, in tabelle 2 x 2 il coefficiente di correzione q di Williams è calcolato con
ed il valore di Gadj dato dal rapporto Gadj = G/q Nel caso di tabelle 2 x 2 è diffusa anche la correzione di Mantel-Haenszel, utilizzata pure in altri casi, come per il calcolo del c2. Consiste nell’aggiungere o togliere 0,5 ad ognuna delle 4 frequenze osservate, sulla base del confronto dei prodotti delle due diagonali: a x d contro b x c. Se il prodotto a x d è maggiore di b x c, - si toglie 0,5 sia ad a che a d e - si aggiunge 0,5 sia a b che a c. Se il prodotto a x d è minore di b x c, - si aggiunge 0,5 sia ad a che a d e - si toglie 0,5 sia a b che a c. Con tali correzioni, sia i totali marginali n1, n2, n3, n4, sia il totale generale N restano invariati.
ESEMPIO . In due appezzamenti di terreno (A e B) con suoli di natura diversa sono stati messi a dimora alberi della stessa specie. Solo una parte di essi ha avuto una crescita normale (+).
Si può affermare che la diversa natura dei due suoli incide sulla crescita normale di tale specie? Confrontare i risultati ottenuti (A) dal test G, con le due (B e C) correzioni proposte, ed il test c2 senza (D) e con la correzione (E) per campioni non grandi. Risposta. A ) Con il metodo G, che ha 1 gdl, scindendo l’operazione in 3 parti, I - quella che riguarda i 4 valori osservati a, b, c, d, II – quella che riguarda i 4 totali marginali n1, n2,n3, n4, III – quella che riguarda il totale generale N, si ottiene:
da cui si stima
un valore di G uguale a 3,88.
B) Con la correzione di Williams
si ottiene un valore di G aggiustato uguale a 3,82.
C) Con la correzione di Mantel-Haenszel, poiché il prodotto di 35 x 26 è maggiore di quello dato da 18 x 23 e quindi i dati osservati devono essere modificati in
si ottiene
da cui
si ottiene un valore di G aggiustato uguale a 3,06.
D) Il c2 con la formula abbreviata per grandi campioni
da un valore uguale a 3,78 con 1 gdl. E) Il c2 con la correzione di Yates per campioni non grandi
da un valore uguale a 3,05. 3.10.3 Tabelle M x N con la correzione di Williams Nel caso di una tabella M x N, la formula per calcolare G è un’estensione di quella già utilizzata per tabelle 2 x 2. Indicando con f le frequenze osservate e spezzando le operazioni in 3 passaggi, con I = å f ln f di ogni casella, II = å f ln f di ogni totale marginale sia di riga che di colonna, III = å N ln N, con N uguale al totale generale del numero di osservazioni, si ottiene il valore di G con G = 2×(I – II +III) In questo caso, la correzione q di Williams in una formula semplice è data da
dove m e n sono il numero di righe e il numero di colonne della matrice, N è il numero totale di osservazioni.
Con la simbologia utilizzata nella tabella seguente, applicata al caso di una tabella 3 x 3,
il modo per calcolare il valore del likelihood ratio è G = [( a1 ln a1 + a2 ln a2 + a3 ln a3 + b1 ln b1 + b2 ln b2 + b3 ln b3 + c1 ln c1 + c2 ln c2 +c3 ln c3 ) - - ( n1 ln n1 + n2 ln n2 + n3 ln n3 + n4 ln n4 + n5 ln n5 + n6 ln n6 ) + (N ln N) ] I gradi di libertà sono (m – 1) x (n – 1), uguali a 2 x 2 = 4 nel caso della tabella precedente.
ESEMPIO. In tre zone di una città (chiamate A, B, C) sono state rilevate varie misure d’inquinamento, da quello acustico a quello atmosferico. Successivamente, dai diversi valori d’inquinamento sono stati derivati punteggi o indici, suddivisi in tre categorie: bassi, medi, alti. Nella tabella sottostante, sono riportate le frequenze delle tre categorie di indici, per ognuna delle tre zone chiamate rispettivamente A, B e C.
FREQUENZE OSSERVATE
Esiste una differenza significativa nella distribuzione dei punteggi delle tre zone? Punteggi bassi, medi e alti hanno la stessa distribuzione percentuale nelle tre zone? (Calcolare il valore del c2 ed il valore del likelihood ratio, confrontando i risultati.) Risposta. L’ipotesi nulla H0 sostiene che la distribuzione dei valori bassi, medi e alti nelle 3 zone è uguale e che le differenze riscontrate sono imputabili solamente a variazioni casuali; in altri termini i livelli d’inquinamento sono indipendenti dalla zona. L’ipotesi alternativa H1 afferma che tra le tre zone esiste una distribuzione significativamente differente dei valori bassi, medi e alti. In altri termini, le tre zone hanno una percentuale differente di valori bassi, medi o alti: esiste associazione tra livelli d’inquinamento e zona E’ un test bilaterale (nei confronti multipli e con i test proposti non sono possibili test unilaterali). FREQUENZE ATTESE
Per il calcolo del c2 e per la successiva interpretazione è utile calcolare la tabella delle frequenze attese, nella condizione che l’ipotesi nulla sia vera. Per i calcoli successivi, è necessario costruire la tabella delle differenze tra valori osservati ed attesi. Serve anche come verifica dei calcoli già effettuati, poiché sia i totali di riga che quelli di colonna ed il totale generale devono essere uguali a zero, ricordando che le frequenze attese sono calcolate a partire dai totali marginali, secondo la relazione
Frequenza attesa in ogni casella = Totale di riga x Totale di colonna / Totale generale
FREQUENZE OSSERVATE - FREQUENZE ATTESE
Il passo successivo è la stima del contributo di ogni casella al valore complessivo del c2. Ogni casella indica la differenza tra frequenza osservata e frequenza attesa, in rapporto alla frequenza attesa.
(FREQUENZE OSSERVATE - FREQUENZE ATTESE)2 / FREQUENZE ATTESE
Si ottiene un valore complessivo del c2(4) uguale a 10,292; la tabella sinottica alla probabilità 0.05 fornisce un valore critico uguale a 9,49. Si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa: fra le tre zone esiste una differenza significativa nella distribuzione degli indici d’inquinamento e quindi associazione tra zone e livelli d’inquinamento. La lettura dei valori del chi quadrato in ogni casella ed il confronto tra distribuzione osservata e distribuzione attesa evidenziano che i contributi più importanti alla significatività sono dati sia da una presenza di valori medi osservati maggiore dell’atteso nella zona B, sia da una presenza di valori bassi nella zona B minori dell’atteso.
L’obiezione più importante che si può rivolgere alla attendibilità delle conclusioni raggiunte con il c2deriva dalle ridotte dimensioni del campione: sono solamente 33 osservazioni in totale, distribuite in 9 caselle delle quali 5 hanno frequenze attese inferiori a 4.
Pertanto può essere richiesto l’uso del metodo likelihood ratio proposto come metodo robusto, da applicare correttamente anche nel caso di campioni piccoli.
Applicato ai dati dell’esempio, il valore del log likelihood ratio è ottenuto mediante
G = 2 x{[(5 x 1,609) + (2 x 0,693) + (1 x 0) + (3 x 1,099) + (10 x 2,303) + (1 x 0) + (5 x 1,609) + + (2 x 0,693) + (4 x 1,386) ] - - [(8 x 2,079) + (14 x 2,639) + (11 x 2,398) + (13 x 2,565) + (14 x 2,639) + 6 x 1,792)]+ + [(33 x 3,497)]}
G = 2 x [(8,045 + 1,386 + 0 + 3,297 + 23,030 + 0 + 8,045 + 1,386 + 5,544) - - (16,632 + 36,946 + 26,378 + 33, 345 + 36,946 + 10,752 ) + (115,409)]
G =2 x (50,733 - 160,999 +115,409) = 2 x 5,143 = 10,286
e fornisce un valore di G uguale a 10,286.
La probabilità è fornita dalla medesima tabella dei valori critici del c2, per gli stessi gradi di libertà.
La correzione q di Williams è
e pertanto il valore di G aggiustato è
uguale a 9,515 per 4 gdl. Il valore critico alla probabilità a = 0.05 è sempre uguale 9,49.
Per quanto riguarda le conclusioni, è importante ricordare che quando il valore calcolato è vicino a quello critico non si deve decidere in modo netto, accettando o rifiutando l’ipotesi nulla con certezza. La risposta del test non è significativa se è appena superiore o appena inferiore al valore critico; si tratta di probabilità e il risultato non è molto differente se la probabilità è appena superiore o appena inferiore al livello critico prescelto: in entrambi i casi, si deve parlare di risposte tendenzialmente significative.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||