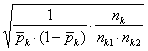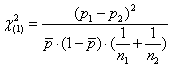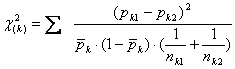CAP III - ANALISI DELLE FREQUENZE

 

 

3.11.   IL CHI QUADRATO CON IL METODO DI COCHRAN E DI MANTEL-HAENSZEL

 

 

Quando si dispone di una serie di tabelle 2 x 2, quindi una distribuzione di frequenze a tre dimensioni, un metodo per valutare l’associazione tra due variabili categoriali, raccomandata da F. Yates nel 1955 (nell’articolo The use of transformations and maximum likelihood in the analysis of quantal experiments involving two tratments, pubblicato su Biometrika, 42, pp. 382-403) e da J. L. Fleiss nel 1970 (On the asserted invariance of the odds ratio, pubblicato su Brit. J. prev. soc. Med., 24, pp. 45-46) è la cosiddetta differenza standardizzata

 

dove

  p₁   e   p₂    sono rispettivamente le frequenze relative dei due campioni a confronto,

     è la media ponderata delle due frequenze relative (vedi cap. III).

 

Estesa a più coppie di gruppi a confronto, come possono essere k tabelle 2 x 2, con misure di associazione la differenza standardizzata diventa

 

e il suo errore standard e.s.(d_k) è

 

e.s.(d_k) =

 

 dal quale si ricava

Derivato dal metodo che, per grandi campioni, utilizza la distribuzione z e sulla base della relazione

il metodo del c² proposto da W. G. Cochran nel 1954 (nell’articolo Some methods of strengthening the common c² tests, pubblicato da Biometrics, vol. 10, pp. 417-451)

 nel caso di due campioni è

 

 e nel caso di k campioni diventa

 

 

Lo stesso risultato è ottenuto con la formula abbreviata

dove w_k e d_k sono calcolati con le formule appena presentate.

 

ESEMPIO.  Un’applicazione di questi concetti può essere tratta dal volume di Joseph L. Fleiss del 1973 (Statistical Methods for Rates and Proportions, John Wiley & Sons, New York, p. IX + 223). L’impostazione dell’esempio è stato leggermente variata, affinché la sua utilizzazione nella ricerca ambientale fosse meglio compresa.

La percentuale di persone con asma o disturbi respiratori in genere è ritenuta un indicatore dell’inquinamento atmosferico; ma questi sintomi possono essere determinati anche da allergie ai pollini, la cui diffusione dipende dalla stagione.  Per valutare la significatività delle differenze tra due zone, tenendo in considerazione la variabilità stagionale, con visite dell’ufficiale sanitario nelle scuole elementari di due zone della stessa città è stata valutata la frequenza di alunni con malattie polmonari, ripetendo la verifica in tre stagioni diverse (autunno, inverno, primavera).

I risultati possono essere presentati con tre tabelle 2 x 2, ognuna relativa ad una rilevazione:

 

Rilevazione  I

 

Rilevazione  II

 

Rilevazione  III

 

Risposta:

I - I dati di queste tre tabelle possono essere presentati in modo più schematico, ma con la stessa quantità d’informazione, in una tabella unica:

Proporzioni di individui affetti da malattie polmonari sul numero di individui campionati

 

 

Essa offre il vantaggio di evidenziare meglio i dati, per quantificare i diversi valori del chi-quadrato con il metodo di Cochran.

 

II - A questo scopo,  con le formule precedenti, si calcolano le quantità riportate nella tabella

 

 

Limitando la dimostrazione dei vari passaggi solo alla II rilevazione

 

1)                              = 0,289 – 0,351 = -0,062

 

2)                                =

 

3)                                =

 

4)                               = 326

 

5)                                =

 

6)                                =  = -5,02

 

7)                                =  = 1,43

 

 

III - L’analisi dei risultati (ultima colonna dell’ultima tabella) permette di concludere che non sono significativi

-          nessuno dei tre valori di chi quadrato (0,54;  1,43;  1,78), ognuno con 1 gdl,

-          né il chi quadrato totale (3,75) con 3 gdl.

 

 

Il test di Cochran permette di scomporre questo chi quadrato con k gdl, quanti sono le tabelle 2 x 2. Con il test  detto per l’omogeneità delle differenze standardizzate, è possibile verificare se le tre rilevazioni hanno dato risposte omogenee o significativamente differenti tra le tre stagioni,

mediante la formula

IV - Con i dati dell’esempio

il chi quadrato per l’omogeneità risulta uguale a 3,605 con 2 gdl; di conseguenza, non è significativo (infatti per a = 0.05 il valore critico del c² è uguale a 5,99).

 

 

V - La significatività della differenza d complessiva tra le due zone nella proporzione di persone ammalate è ottenuta attraverso la stima di d

 

e del suo errore standard  e.s.(d)

 

Il valore del chi quadrato per verificare la significatività di questa differenza media standardizzata,

cioè dell’associazione tra malattia e zona in complesso è

 

risulta uguale a 0,146 con 1 gdl.

La conclusione è che non esiste una differenza significativa nella frequenza relativa di ammalati nelle due zone. Tenendo presente i diversi gdl, si può sostenere che è maggiore la differenza tra stagioni che tra zone, seppure nessuna delle due sia risultata significativa.

 

Il metodo del c² proposto da N. Mantel e W. Haenszel nel 1959 (con l’articolo Statistical aspects of the analysis of data from  retrospective studies of disease pubblicato su J. Matl. Cancer Inst., 22, pp. 719-748), reso più generale da N. Mantel nel 1963 (con l’articolo Chi-square tests with one degree one freedom. Extension of the Mantel-Haenszel procedure, pubblicato su Journal of the American Statistical Association, vol. 58, pp.690-700)  può essere visto come la correzione di quello di Cochran per piccoli campioni.

 

Utilizzando la stessa impostazione di Cochran, nella parte finale

 

apporta una correzione

-          sia a w_k

-          sia a d_k

 

togliendo 1 a n_k, (il numero di osservazioni del gruppo k).

 

Quando il numero di dati è grande, la differenza dal metodo precedente è assolutamente trascurabile; diviene relativamente importante, quando il campione è di piccole dimensioni.

Utilizzando gli stessi dati dell’esempio precedente, si ottiene la correzione delle colonne

d_k   e   w_k

 

 

Poiché il campione utilizzato può essere considerato grande, se il calcolo è effettuato con due sole cifre decimali, il valore del chi quadrato di ogni rilevazione e quello totale (3,78) restano invariati.