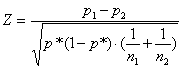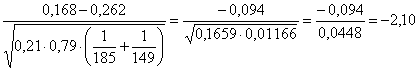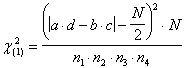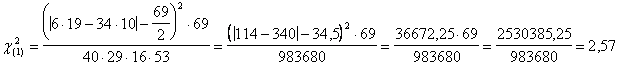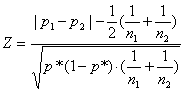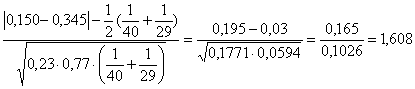CAP III - ANALISI DELLE FREQUENZE

 

 

3.6.   CONFRONTO TRA TEST   PER TABELLE 2 X 2   E   TEST Z, SENZA E CON LE CORREZIONI PER LA CONTINUITA’

 

 

Il test Z ed il test   ₍₁₎ per tabelle 2 x 2 possono essere applicati negli stessi casi.

Il confronto tra due percentuali con il test Z  ed il confronto tra due distribuzioni osservate in tabelle di contingenza 2 x 2 con il test  forniscono la stessa risposta.  Tra test t e test c² sono differenti la presentazione dei dati ed ovviamente i valori calcolati; ma le ipotesi da verificare sono le stesse e dovrebbero coincidere anche le probabilità stimate, a meno delle approssimazioni dei calcoli nei due differenti metodi. Le probabilità stimate divergono quando i campioni hanno poche osservazioni; ma in questi casi, con campioni piccoli, è in discussione la validità dei due test.

Come è possibile dedurre osservando la formula di Pearson, la distribuzione dei valori c² con 1 g.d.l. è la distribuzione di quadrati di variabili casuali normali standardizzate, dove la standardizzazione è ottenuta dividendo la differenza (al quadrato) tra osservato ed atteso per la frequenza assoluta attesa. Si ottiene un rapporto che, come tale, è indipendente dal numero assoluto di osservazioni.

In termini matematici, si può scrivere che

Z² @ c²₍₁₎

 

Per n variabili casuali normali standardizzate ed indipendenti, come sono i gruppi a confronto in un test chi quadrato, la somma dei quadrati segue la distribuzione c² con n gradi di libertà, secondo la relazione

 

ESEMPIO 1.  I popolamenti zooplanctonici dei laghi artificiali sono in prevalenza composti da Cladoceri e Rotiferi; mentre nei grandi laghi naturali predominano i Copepodi.

Cladoceri e Rotiferi trovano nei laghi artificiali, di recente formazione e con instabilità idrologica, le condizioni migliori per sfruttare la loro strategia r di colonizzazione; i Copepodi, con la loro strategia k, sono avvantaggiati in ambienti caratterizzati da elevata stabilità, come i grandi laghi naturali.

In due campioni di popolamenti zooplanctonici sono stati contati i Copepodi ed insieme Cladoceri e Rotiferi.

Nel campione 1  i Copepodi erano 31, mentre Cladoceri e Rotiferi insieme erano 154; nel campione 2 sono risultati presenti 39 Copepodi contro 110 Cladoceri e Rotiferi.

Si può affermare che i Copepodi siano più facilmente associati ad uno dei due laghi?

 

Risposta. E’ un test bilaterale (d’altronde con il test  c² sono possibili solo test bilaterali).

L’ipotesi nulla è  H₀: p₁ = p₂

e l’ipotesi alternativa è   H₁: p₁ ¹ p₂

Per applicare il test c² con 1 g.d.l., è utile presentare i dati in una tabella di contingenza 2 x 2, completando le informazioni sui dati. Spesso alcuni di essi non sono espressamente riportati nel testo del problema, in quanto inutili alla comprensione dell’argomento e facilmente deducibili dagli altri. Per il calcolo è indispensabile che siano riportati tutti con la stessa evidenza.

Con i dati presentati, la tabella 2 x 2 diviene

 

 

	Copepodi	Cladoceri e Rotiferi	Totale
Lago  1	31	154	185
Lago  2	39	110	149
Totale	70	264	334

 

E’ un campione di grandi dimensioni e conviene utilizzare la formula generale per il calcolo rapido,

 

 senza correzione per la continuità

 

 dal quale risulta  ₍₁₎ =  4,41.

Nella tabella sinottica del ₍₁₎  ad un valore di 4,41 corrisponde una probabilità compresa tra 0.05 (il cui valore critico esatto è 3,84) e 0.025 (il cui valore critico esatto è 5,02).

 

Per lo stesso problema è possibile utilizzare il test Z, ricorrendo alla formula generale

 

 con i dati richiesti;

 dove:    p₁ = 0,168;   p₂ = 0,262;   n₁ = 185;   n₂ = 149;  

 m₁ = 31;   m₂ = 39;                                                                    p* =  = 0,210

Il valore di Z ottenuto dal calcolo

 

Z =

 

 risulta uguale a -2,10. Nella tabella della distribuzione normale standardizzata ad una coda, al valore 2,10 in una coda corrisponde una probabilità uguale a 0.018; per un test bilaterale, la probabilità è uguale a 0.036 (quindi coincidente con la risposta del chi quadrato che dava una probabilità compresa tra 5% e 2,5%).

E’ una misura più precisa di quella possibile con il test chi quadrato, soltanto perché nella tabella sinottica (riassuntiva) dei valori critici del chi quadrato sono riportati solamente alcuni di quelli ritenuti più importanti. Esistono tante distribuzioni c² quanti sono i gradi di libertà; servirebbero quindi tante pagine, quanti sono i gradi di libertà.

Di conseguenza, si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa. Secondo l’interpretazione ecologica del risultato, la presenza percentuale di Copepodi (e simmetricamente di Cladoceri più Rotiferi) nei due laghi è significativamente differente.

Con il test Z, il segno negativo della differenza indica che è maggiore la presenza di Cladoceri nel lago 2. Con il test chi quadrato, per evidenziare le frequenze osservate che hanno determinato la significatività è utile costruire la tabella delle frequenze attese.

Con il test Z è stata posta l’attenzione sulla proporzione dei Copepodi. Si fosse impostato il problema sulla proporzione di Cladoceri e Rotiferi, il risultato sarebbe stato identico: identica sarebbe stata la differenza tra le due proporzioni, riportata al numeratore; identico sarebbe stato l’errore standard della differenza, riportato al denominatore.

Come verifica della relazione

Z² @ c²₍₁₎

 anche con i dati di questo esempio è possibile osservare che il valore del test Z (uguale a - 2,10) elevato al quadrato (-2,10² = 4,41) è esattamente uguale al valore calcolato con il test c²₍₁₎ (uguale a 4,41)

- 2,10² @ 4,41

 

ESEMPIO 2.   In una seconda serie di conteggi, nel campione pescato nel lago 1 sono stati classificati 6 Copepodi e 34 tra Cladoceri e Rotiferi, mentre nel campione del lago 2 sono stati classificati 10 Copepodi e 19 tra Cladoceri e Rotiferi.

Si può sostenere che la percentuale di Copepodi, oppure quella di Cladoceri e Rotiferi insieme, riscontrata nei due laghi sia significativamente differente?

 

Risposta.   E’ un test bilaterale, dove l’ipotesi nulla è  H₀: p₁ = p₂

 e l’ipotesi alternativa è   H₁: p₁ ¹ p₂

Riportati in una tabella 2 x 2, i dati dei due campioni a confronto sono:

 

	Copepodi	Cladoceri  e Rotiferi	Totale
Lago  1	6	34	40
Lago  2	10	19	29
Totale	16	53	69

 

Il numero totale di osservazioni è 69: non è un campione di grandi dimensioni e si richiede la correzione di Yates. La formula con la quale abbreviare i tempi necessari per i calcoli manuali è

 

Con i dati del problema,

 

fornisce un _{(1)  =}  2,57.

Nella tabella sinottica del  ₍₁₎ al valore 2,57 corrisponde una probabilità a compresa tra 0.10 ( il cui valore critico è 2,706) e 0.25 (il cui valore critico è 1,323);  purtroppo, è una stima molto approssimata, a causa dei pochi valori critici di norma riportati nelle tavole sinottiche. 

 

Per il medesimo problema, con gli stessi dati è possibile ricorrere al test Z per il confronto tra percentuali, ricorrendo alla formula con la correzione per la continuità di Yates

 

dove:

   p₁ = 0,150;   p₂ = 0,345;   n₁ = 40;   n₂ = 29;   m₁ = 6;   m₂ = 10;

 e

p* =  = 0,232

 si stima un valore di Z

 

Z =

 

 che risulta uguale a 1,608.

Nella tabella della distribuzione normale standardizzata ad una coda, Z = 1,61 (arrotondamento di 1,608) esclude una densità di probabilità a = 0.055; per un test bilaterale, la probabilità è a = 0.11 (11,0%).

 

E’ semplice osservare che 1.608 è approssimativamente uguale a 2.58: il test c², con un grado di libertà, ed il test Z, per il confronto tra due percentuali, forniscono risultati molto simili, nonostante le approssimazioni nei calcoli determinate dalle due diverse formule e le distorsioni determinate dal numero ridotto di dati.

Comunque, la probabilità stimata con i due calcoli è alta, nettamente superiore al 5%. Pertanto, la differenza non è significativa e non si può rifiutare l’ipotesi nulla: la percentuale di Copepodi (e simmetricamente di Cladoceri e Rotiferi) riscontrate nei due laghi non è significativamente diversa e differisce solo per fattori casuali.

 

Per meglio comprendere i concetti fondamentali dell’inferenza statistica, è importante osservare come, con i dati di questo secondo esercizio, la differenza tra le due percentuali sia maggiore rispetto a quella del primo esercizio (p₁-p₂ = 0,126 rispetto a 0,094); eppure, diversamente dal caso precedente, non si è in grado di rifiutare l’ipotesi nulla. La causa è il più ridotto numero di osservazioni, per cui le variazioni casuali sono notevolmente maggiori. Con pochi dati, il test è poco potente (la potenza del test sarà discussa nel successivo capitolo 4): non si è in grado di rifiutare l’ipotesi nulla, anche quando è evidentemente falsa.

Non essere in grado di rifiutare l’ipotesi nulla non significa che le due percentuali siano uguali.

Se si fosse convinti della reale esistenza di una differenza tra le due percentuali, per rendere il test significativo sarebbe sufficiente aumentare il numero di osservazioni. Quando il numero di osservazioni è molto grande, risultano significative anche differenze molto piccole.