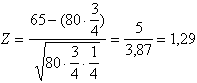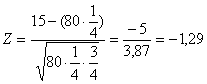CAP III - ANALISI DELLE FREQUENZE

 

 

3.7.   CONFRONTO DI UNA  PROPORZIONE OSSERVATA CON UNA ATTESA: IL TEST Z PER GRANDI CAMPIONI E LA DISTRIBUZIONE BINOMIALE PER PICCOLI CAMPIONI

 

 

La distribuzione Z (presentata nel capitolo 2) permette anche il confronto tra la proporzione osservata in un singolo esperimento e la corrispondente proporzione attesa o teorica.

La formula può essere derivata da quella già utilizzata per la distribuzione di una osservazione campionaria  x  rispetto alla media della popolazione m, quando sia nota la varianza s² della popolazione, attraverso la relazione

 

poiché la varianza di una proporzione è totalmente definita dal suo valore medio p e dal numero totale di osservazioni essendo  s² = n × p × (1-p)

 

Nel caso di una proporzione, il test Z diventa

 

ricordando che:

-          p = proporzione attesa o teorica,

-          n = numero totale di osservazioni o dati dell’esperimento;

-          x = numero di individui osservati con la caratteristica in esame;

-          n × p = numero atteso di individui con la caratteristica in esame.

 

Nel test Z, la distribuzione delle probabilità è simmetrica ed il risultato evidenzia se la differenza è positiva oppure negativa. L’ipotesi alternativa H₁ può essere non solo bilaterale ma anche unilaterale.

 

ESEMPIO 1.   In un esperimento di incroci nel pisello, da una pianta eterozigote sono state ottenuti 65 semi lisci e 15 semi rugosi. Secondo le leggi di Mendel, il rapporto atteso di 3/4 e 1/4 avrebbe dovuto dare 60 semi della prima caratteristica e 20 della seconda.

Il numero di semi lisci si discosta dal valore atteso di 3/4?  Questa distribuzione sperimentale segue la legge di segregazione di Mendel?

 

Risposta.  L’ipotesi nulla H₀ afferma che il numero osservato (65) è in sostanziale accordo con quello atteso (60 = 80 x 3/4), stimato sulla base della legge di Mendel; la differenza riscontrata tra frequenza osservata e frequenza attesa è un fenomeno altamente probabile, imputabile solamente a fattori casuali.

L’ipotesi alternativa H₁ afferma che il numero osservato si discosta molto da quello atteso; la differenza riscontrata non è dovuta a fattori casuali, ma al fatto che la distribuzione osservata non segue la legge di Mendel. E’ un test bilaterale.

 

La probabilità complessiva di trovare scarti tra osservato ed atteso che siano uguali o superiori a quello riscontrato nell’esperimento può essere calcolata mediante il test Z

 

dove:   x = 65;   n = 80;   p = ¾.  

Con i dati dell’esempio, si può stimare il valore di Z,

 

che risulta uguale a  1,29.

Il valore calcolato di Z è inferiore a quello tabulato per la distribuzione normale alla probabilità del 5% (1,96), in un test a due code. Di conseguenza, non si può rifiutare l’ipotesi nulla: le differenze riscontrate tra osservato ed atteso sono imputabili solamente a variazioni casuali. La proporzione osservata (65/80 = 0,8125) è in sostanziale accordo con la proporzione di 3/4 della legge di Mendel.

 

La domanda avrebbe potuto essere impostata sulla frequenza del fenomeno alternativo, quella del numero di semi rugosi, che sono risultati 15 su 80 (15/80 = 0,1875) quando la proporzione attesa sarebbe stata di 1/4.

Il valore ottenuto con il test Z sarebbe stato identico, ovviamente con segno opposto, come mostra il calcolo

 

 

ESEMPIO 2.  Per il materiale dei loro esperimenti a carattere biologico con cavie, semi o uova, l’ecologo e l’ambientalista spesso si riforniscono da ditte specializzate. Queste, a testimonianza della qualità del loro prodotto, assicurano la sopravvivenza di una certa percentuale o proporzione di individui per un periodo definito, in condizioni standard.

Da 150 semi, di cui era stata garantita una riuscita del 90%, ad un ricercatore sono spuntate 122 pianticelle. E’ una percentuale di successi di poco superiore a 81%, contro il 90% atteso.

Si può sostenere che non esiste una differenza significativa con l’atteso oppure che il numero di pianticelle è effettivamente minore di quanto era stato assicurato?

 

Risposta. E’ un test ad una coda, in cui l’ipotesi nulla afferma che la differenza è trascurabile, mentre l’ipotesi alternativa sostiene che la percentuale trovata è significativamente minore di quella attesa.

 

Il test Z, dove  x = 122;  p = 0,9;  n = 150

 

 stima un valore uguale a -3,53. Nella tabella della distribuzione normale standardizzata, in una coda corrisponde ad una probabilità inferiore a .00023.

Si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa: la percentuale di riuscita è significativamente inferiore a quella attesa. Le pianticelle non hanno avuto la riuscita che era stata garantita.

 

Il test   ed il test Z non sono gli unici metodi per testare la significatività di una differenza tra proporzioni, quando il campione non è piccolo.  E’ anche possibile usare i limiti di confidenza di una proporzione (presentati nel capitolo 4).

 

Nel caso di una frequenza relativa con campioni piccoli, come quando n×p oppure n×(1-p) è inferiore a 5 (e a maggior ragione quando entrambi sono inferiori a 5), occorre risolvere il problema in modo esatto con la distribuzione binomiale.

La distribuzione binomiale (presentata nel capitolo 2)

 

 

 permette di stimare la probabilità esatta di avere la risposta i in oggetto.

A differenza del test Z, che fornisce un valore al quale nella distribuzione normale ridotta è associata la probabilità di avere valori uguali o superiori  a quello calcolato, con la distribuzione binomiale si ottiene direttamente la probabilità che si realizzi una specifica risposta. Per rifiutare l’ipotesi nulla, questa probabilità deve essere cumulata con tutte quelle associate alle possibili risposte più estreme.

 Quando si ha un test unilaterale, per ottenere  la probabilità complessiva che permette di rifiutare l’ipotesi nulla occorre sommare la probabilità associata all’evento osservato con tutti i possibili eventi più estremi nella stessa direzione.

Quando si ha un test bilaterale, occorre moltiplicare per 2 il valore precedentemente calcolato, perché le possibili risposte più estreme sono collocate in entrambe le direzioni.

 

ESEMPIO. E’ possibile fornire una prima stima dell’attività biologica di una sostanza, mediante test di tossicità acuta condotti in tempi brevi, di norma tra le 24 e le 96 ore di esposizione. Si ottengono informazioni sugli effetti tossici immediati di immissioni, più o meno accidentali, in ambiente acquatico. Le sostanze impiegate in questi test vanno dai pesticidi a quelle contenute in rifiuti industriali e domestici. Le specie animali utilizzate vanno dai pesci agli invertebrati, mentre le specie vegetali utilizzate di solito sono microalghe.

Con numerosi esperimenti, è stato dimostrato che le immissioni in ambiente acquatico di un corso d’acqua determina, in esperimenti di laboratorio, la mortalità del 40% dei pesci dopo una esposizione di 48 ore.

Nell’ultimo monitoraggio, le sostanze immesse determinavano un colore del corso d’acqua più vistoso ed un odore più acuto, lasciando supporre una maggiore concentrazione di sostanze tossiche. L’esperimento di laboratorio ha determinato la mortalità di 8 animali sui 9 esposti al rischio.

Si può statisticamente sostenere che le ultime emissioni contengono sostanze con un effetto tossico significativamente superiore a quello di norma riscontrato?

 

Risposta.  E’ un test ad 1 coda; ma l’ipotesi deve essere formulata a priori, rispetto ai risultati dell’esperimento. Non è corretto guardare i risultati dell’esperimento e chiedersi se è significativamente superiore alla media, solamente dopo aver osservato che la percentuale di letalità supera il risultato medio.

Nell’esempio, l’ipotesi nulla H₀ afferma che la percentuale di letalità riscontrata nell’ultima rilevazione (8/9 = 0.89) è una variazione casuale della percentuale di solito riscontrata, uguale a 0.4; l’ipotesi alternativa H₁ afferma che la letalità delle sostanze campionate nell’ultimo monitoraggio è significativamente superiore alla media.

La scelta tra le due ipotesi dipende dalla probabilità complessiva stimata.

Per calcolare la probabilità complessiva che permetta di decidere tra le due ipotesi, dapprima si deve calcolare la probabilità di ottenere la risposta osservata di 8 decessi (P₈), con i dati del problema, dove

n = 9;   i = 8; p = 0.4

ma essa non è la risposta più estrema. Nella stessa direzione, si sarebbe avuto un effetto ancora più letale, se fossero morti tutti 9 gli animali utilizzati nell’esperimento. 

 

Con   n = 9; i = 9; p = 0.4,  la  probabilità  di ottenere per caso anche questo risultato (P₉ ) è

La probabilità complessiva di ottenere la risposta osservata oppure una risposta più estrema nella stessa direzione è data dalla somma di queste due singole probabilità

P₈₊₉ = 0.00354 + 0.00026 = 0.0038 (0,38%).

Una probabilità  uguale a 0,38% deve essere considerata molto piccola: si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa.

Come indicavano il colore più evidente e l’odore più sgradevole, la letalità (0.89 con 9 osservazioni) delle sostanze tossiche presenti nell’immissione è significativamente più alta della letalità media (0.4) degli esperimenti precedenti.

Se il quesito avesse avuto un’ipotesi alternativa bilaterale, per ottenere la probabilità relativa si sarebbe dovuto moltiplicare questa probabilità per 2.