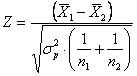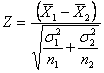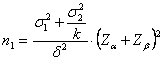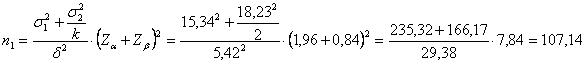VERIFICA DELLE IPOTESI

TEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTA

E TEST SULLA VARIANZA

CON INTERVALLI DI CONFIDENZA

4.11. POTENZA E NUMERO DI DATI PER LA SIGNIFICATIVITA’ DELLA DIFFERENZA TRA DUE MEDIE, CON LA DISTRIBUZIONE NORMALE;

Per effettuate un test Z sulla significatività della differenza tra le medie di due campioni indipendenti,

- quando le due varianze e sono uguali e dove è la varianza comune (pooled) dei due campioni, si utilizza

- mentre quando le due varianze e sono differenti,

si utilizza

In entrambi i casi, è possibile calcolare a priori il numero minimo di dati in ognuno dei due gruppi,

- affinché la differenza attesa

- risulti significativa alla probabilità a e con rischio b,

Nel primo caso, quando le due varianze e sono uguali,

- la stima di può essere ricavata

per ogni gruppo

Nel secondo, quando le due varianze e sono differenti,

- la stima di può essere ricavata

per ogni gruppo

ESEMPIO 1. (USO DELLA FORMULA CON VARIANZE DIFFERENTI, tratto con modifiche da Bernard Rosner, 2000, Fundamentals of Biostatistics, 5^th ed. Duxbury, Thomson Learning, XIX + 992 p. a pag. 307).

Uno studio pilota, per preparare un test bilaterale sulla differenza tra le medie di due campioni indipendenti, ha dato i seguenti risultati

= 132,86 = 127,44 = 15,34 = 18,23 = 8 = 21

Se le statistiche dei dati campionari raccolti sono assunti come stime corrette dei parametri delle due popolazioni, quanti dati occorre raccogliere per ogni gruppo, affinché

- in un esperimento nuovo e con un rischio b = 0,20

- un test bilaterale sulle due medie risulti significato alla probabilità a = 0.05?

Risposta. Con = 132,86 – 127,44 = 5,42 e gli altri parametri già definiti nella domanda, oltre a

- = 1,96 per a = 0.05 in una distribuzione bilaterale,

- = 0,84 per = 0.20 in una distribuzione unilaterale,

si stima

che servono almeno = 152 dati per gruppo, quindi in totale = 304.

In altri testi, è presentata una soluzione differente, fondata sull’analisi statistica delle due varianze campionarie. Attualmente è il metodo più utilizzato; è presentato in modo dettagliato nel capitolo sul test t di Student. La metodologia può essere esposta nei suoi passaggi logici fondamentali:

1 – Si verifica se le due varianze campionarie e sono statisticamente differenti.

I metodi più noti sono tre: a) il test F, dato dal rapporto tra la varianza maggiore e quella minore; b) il test di Bartlett, fondata sulla distribuzione chi quadrato; c) il test di Levene, che utilizza gli scarti di ogni dato dalla sua media di gruppo.

2 - Se il test prescelto con ipotesi nulla H₀: non risulta significativo, si può assumere che le due varianze siano uguali.

3 – Si ricava la varianza comune, utilizzando le due devianze e i rispettivi gradi di libertà,

come

Applicata ai dati campionari dell’esempio

4 – Usando questa ultima come varianza reale , con gli stessi parametri precedenti,

si ottiene una stima di = 163,93 arrotondata a 164.

E’ un valore maggiore del precedente = 152.

In questa ultima formula, la varianza maggiore e quella del campione maggiore hanno un peso più rilevante sulla varianza comune. E, in questo caso, il campione di dimensioni maggiori ha pure varianza maggiore. Quando metodi differenti forniscono risposte non coincidenti, è sempre consigliato fare la scelta più prudenziale. Per le dimensioni del campione, significa scegliere il numero maggiore.

Nei test che confrontano le medie di due o più gruppi, un concetto molto importante nella distribuzione del numero di osservazioni totale è che il test raggiunge la potenza massima, quando i campioni sono bilanciati, cioè hanno tutti lo stesso numero di osservazioni ().

Dalla formula

è facile dedurre che la quantità Z è massima quando

la quantità

è minima.

Situazione che si realizza quando, per lo stesso , si ha .

Ma è una condizione che non sempre conviene rispettare quando nella scelta del numero di dati per ogni gruppo entrano in gioco altri parametri, in particolare il diverso costo morale o economico delle osservazioni dei due gruppi. Anche questi concetti verranno sviluppati ulteriormente nel capitolo sul test t di Student.

Un costo morale differente tra due campioni si ha quando, ad esempio, per valutare l’effetto di un farmaco,

- a un gruppo di ammalati si somministra il farmaco che si ritiene migliore,

- all’altro gruppo di ammalati il farmaco vecchio, ritenuto meno efficace, se non addirittura il placebo.

E’ evidente che somministrare un placebo a un ammalato, lasciandogli credere che sia il farmaco, allo scopo di avere misure certe di confronto e così favorire la scelta della cura migliore, ha costi morali elevati.

Una cautela moralmente obbligata è

- ridurre il numero al minimo il numero di persone alle quali somministrare il placebo,

- ma effettuando un test ugualmente potente.

Sovente, i due gruppi hanno semplicemente costi economici diversi, per i quali è facile definire il loro rapporto. Ad esempio, può essere la raccolta di dati ambientali in un’area vicino a casa e altri in un’area distante, che richiede spese di trasporto maggiori e più tempo. Definito il rapporto tra i due diversi costi, indicato con k, si costruiscono due campioni non bilanciati. Il problema ha varie soluzioni. Un metodo, riportato in alcuni testi, consiste nel

- fissare , definito come il rapporto tra il costo complessivo di ognuno dei due gruppi,

- calcolare , il numero di dati del primo campione

con

- calcolare , il numero di dati del secondo campione,

con

In modo più semplice, la scelta di può dipendere dal rapporto che si vuole ottenere tra le dimensioni dei due campioni

come quello degli ammalati ai quali somministrare il farmaco e quello ai quali dare il placebo .

ESEMPIO 2 (Tratto, con modifiche, da Bernard Rosner, Fundamentals of Biostatistics, 5^th ed. Duxbury, Thomson Learning, 2000, XIX + 992 p. a pag. 308 e con gli stessi dati dell’esempio 1).

Con

= 132,86 = 127,44 = 15,34 = 18,23 = 8 = 21

quanti dati occorre raccogliere per ogni gruppo, affinché

- con

- e un rischio b = 0,20

- alla probabilità a = 0.05

un test bilaterale sulle due medie risulti significativo?

Risposta. Con = 132,86 – 127,44 = 5,42 e gli altri parametri già definiti, oltre a

- = 1,96 per a = 0.05 in una distribuzione bilaterale

- = 0,84 per = 0.20 in una distribuzione unilaterale

per il campione 1

si stima = 107,14

e per il campione 2, più rapidamente,

si ricava = 214,28

ovviamente entrambi arrotondati all’unità superiore ( e ).

Con la formula utilizzata per il campione 1, se applicata al campione 2,

si sarebbe stimato ugualmente = 214,28

Con qualsiasi sbilanciamento, come questo provocato dal rapporto , il numero di dati complessivo aumenta. Confrontando i risultati di questi due esempi, è semplice osservare che

- con due campioni bilanciati servirebbero in totale = 304 (152 + 152)

- con due campioni differenti servirebbero in totale = 323 (108 + 215)

per due test che hanno stessa potenza. Infatti sono stati calcolati per valori identici di a e b.

Questi risultati permettono di cercare la soluzione migliore, quando i dati dei due gruppi, come ipotizzato in precedenza, non hanno gli stessi costi. Se si tratta di costi morali, è ovvio che è meglio dare il placebo solamente a 108 individui invece che a 152.

Se si tratta di costi economici, ad esempio con un rapporto = 2 fondato sul fatto che,

- il costo di ogni dato del campione 1 è di 20 euro,

- il costo di ogni dato del campione 2 è di 10 euro,

è semplice calcolare che

- con due campioni bilanciati il costo complessivo sarebbe stato di 4560 euro (152 x 20 + 152 x 10)

- con due campioni differenti il costo complessivo sarebbe stato di 4310 euro (108 x 20 + 215 x 10)

Altre volte, il numero totale di osservazioni che è possibile raccogliere è prefissato, poiché l’ammontare totale della spesa è già stabilito e i costi per ogni osservazione dei due gruppi sono uguali.

Conoscendo N,

- la suddivisione ottimale nei due gruppi dipende dalle due deviazioni standard e

- e conviene rendere maggiore il gruppo con la deviazione standard maggiore,

secondo il rapporto

in modo da avere per quel gruppo un errore standard proporzionalmente minore.

Ovviamente, se = = , si ha anche = =

Quando

- le due varianze sono uguali ( = = ) e

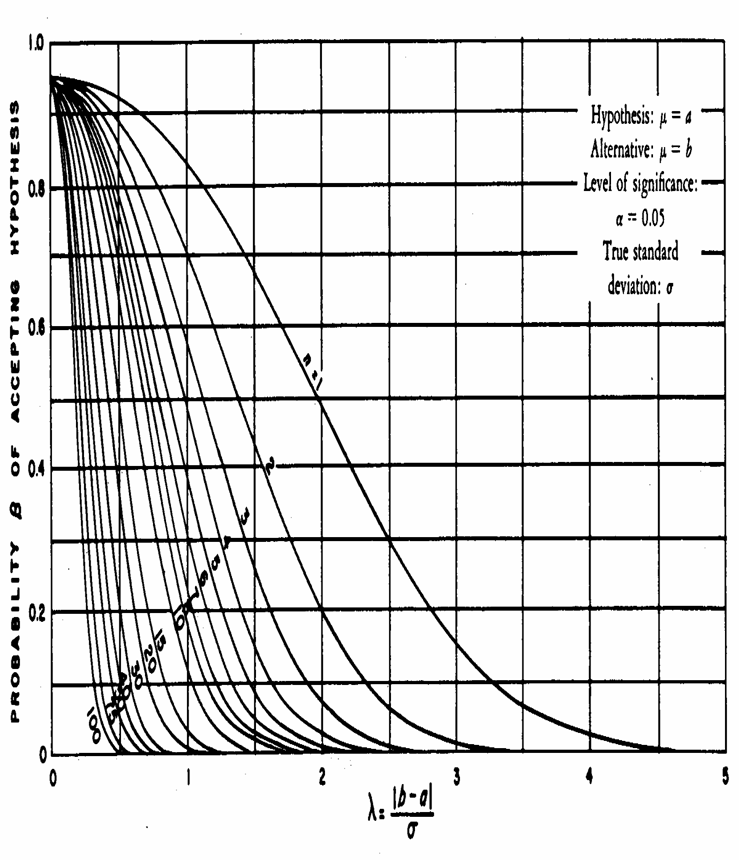
- i due campioni sono bilanciati ( = = ),

è possibile ricorrere anche a metodi grafici, che forniscono risposte approssimate, quando il campione è grande a causa della difficoltà di leggere con precisione i grafici.

La metodologia è del tutto analoga a quella già illustrata in precedenza per un campione,

- ma con un calcolo differente del parametro l.

Con la figura riportata nella pagina precedente, (utile solamente per un test bilaterale, con a = 0.05) è possibile stimare

a) il rischio b,

b) la quantità , il numero minimo di dati necessari in ogni gruppo,

dopo aver calcolato il parametro l attraverso la relazione

dove

- è la differenza teorica d riportata nell’ipotesi nulla H₀, (); si ha d = 0 quando l’ipotesi nulla è H₀: ;

- è la differenza campionaria , che si vuole dimostrare essere significativa;

- è la deviazione standard vera, che in questo caso è data da .

A - Per stimare il rischio b,

- dopo aver individuato il valore di l sull’asse delle ascisse,

- si sale verticalmente fino a incontrare la curva in un punto;

- trasferito orizzontalmente sull’asse delle ordinate, esso indica il rischio b.

B - Per stimare le dimensioni minime () del campione,

- dopo aver individuato il valore di l sull’asse delle ascisse si sale verticalmente

- e dopo aver prefissato il valore di b ci si sposta in modo orizzontale:

- il punto di incrocio dei due segmenti ortogonali individua la curva .

ESEMPIO 3 (Tratto, con modifiche, da pag. 54 del manuale del dipartimento di ricerca della marina militare americana, pubblicato nel 1960: Statistical Manual by Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, Research Department U. S: Naval Ordnance Test Station, Dover Publications, Inc., New York, XVII + 288 p.).

Parte I - La quantità di principio attivo immesso nel prodotto da due aziende farmaceutiche, misurato su due campioni di 4 dati, è stato = 15,60 e = 15,65 con deviazione standard comune = 0,04. Quale è la potenza di questo test bilaterale, affinché la differenza tra le due medie risulti significativa con una probabilità a = 0.05?

Risposta. Usando la formula

dove

= 0,05 = 0,00 = 0,04 = 4 = 0.05 bilaterale

si ricava

un valore = 0,88.

Nella figura precedente, prendendo sull’asse delle ascisse il valore = 0,88 e

- salendo verticalmente, si incontra la curva per = 4 in un punto

- che, trasferito orizzontalmente sull’asse delle ordinate, indica = 0,55.

In questo confronto, per trovare una differenza significativa tra le medie di due campioni indipendenti, il test ha un rischio = 0,55 e quindi una potenza = 0,45.

Parte II - Se si vuole che il test risulti significativo ma con una potenza non inferiore all’80 per cento (quindi = 0,20), quanti dati occorre raccogliere per ogni campione?

Risposta. Sempre nella stessa figura,

- si prende sull’asse delle ascisse il valore = 0,88 e si sale verticalmente,

- contemporaneamente sull’asse delle ordinate si prende = 0,20 e ci si sposta orizzontalmente;

- queste due rette si incontrano in un punto, che cade sulla curva = 10.

Per ognuno dei due campioni servono almeno 10 dati.

Parte III - (CONFRONTO TRA IL RISULTATO DELLA FIGURA E DISTRIBUZIONE Z). Per una valutazione dei due metodi, è interessante confrontare il risultato ottenuto dal grafico con quello della distribuzione Z. Utilizzando

con

= 0,05 = 0,04 per , per ,

si ricava

la stima per ogni campione.

Coincide con la risposta precedente.