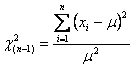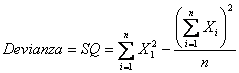VERIFICA DELLE IPOTESITEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTAE TEST SULLA VARIANZA CON INTERVALLI DI CONFIDENZA
4.13. SIGNIFICATIVITA’ DELLA DIFFERENZA TRA UNA VARIANZA
CAMPIONARIA
Nella ricerca scientifica e nelle applicazioni industriali della statistica non sempre l’attenzione è posta sulla media o sulla differenza tra due medie, come nei paragrafi precedenti. In varie situazioni sperimentali, è utile analizzare la variabilità. In modo più specifico, si richiede: - il confronto
della varianza di un campione - la misura dell’intervallo di confidenza di una varianza, - il confronto tra
le varianze di due campioni indipendenti Nei capitoli successivi, saranno presentati anche i metodi per il confronto tra le medie e le varianze di più campioni, sia dipendenti che indipendenti.
Spesso le misure della varianza e le sue analisi sono più importanti delle misure della media e delle sue analisi, anche se queste ultime ricorrono con frequenza nettamente maggiore e quasi tutta la statistica è finalizzata a questo ultimo scopo. Ad esempio, in genetica stime della varianza e confronti tra quelle di due o più gruppi sono utili per lo studio di una caratteristica quantitativa: una varianza minore significa maggiore omogeneità genetica del gruppo campionato. Se si intende selezionare individui con valori medi progressivamente migliori, è utile iniziare da un gruppo che presenti una variabilità elevata. Nella ricerca ambientale, la maggiore o minore variabilità dei livelli d’inquinamento presenti in un’area influisce sulla probabilità che i valori superino i limiti di legge, a parità di valori medi e degli altri parametri della distribuzione. Una media con variabilità piccola è più facilmente accertabile di una con variabilità grande e i risultati sono più prevedibili. Nell’industria e nelle analisi di laboratorio, lo studio della variabilità è utile anche per vagliare la precisione di uno strumento, la qualità di un reagente o l'attendibilità di una procedura. Esse sono migliori quando le risposte sperimentali sono più stabili, quindi le loro varianze sono minori. Ricordando che - la varianza
di una popolazione
- la varianza di un campione
un metodo per esaminare e confrontare statisticamente la varianza di un campione con una varianza teorica utilizza la distribuzione c2. Come già presentato
nel capitolo relativo, quando si dispone di conteggi o frequenze assolute, il
valore c2 di
La sua distribuzione - è una funzione di probabilità - che varia da zero all’infinito positivo - e serve per valutare la variabilità (cioè la
differenza: Osservato – Atteso) di - considerando i gradi di libertà (quasi sempre
uguali a
In una popolazione normale standardizzata, quindi in un modello teorico che consideri la popolazione, l’ultima formula può essere scritta come
poiché - la frequenza
osservata ( - la frequenza
attesa ( Inoltre, dal
capitolo sulle distribuzioni teoriche, è importante ricordare che in una distribuzione
poissoniana, dove la probabilità - quindi con - si ha che la
media
Ne consegue che,
con - la devianza di un campione può essere scritta - come
e che la formula iniziale del c2 diventa
Queste due ultime formule evidenziano un concetto importante: - il c2 con gdl - tra la devianza
di un campione di - e la varianza
vera o della popolazione:
Il confronto tra una varianza
campionaria - con un test bilaterale, con ipotesi H0: s2 = s20 contro H1: s2 ¹ s20
In essa, il
rapporto tra la varianza osservata (s2) e quella attesa secondo
l'ipotesi nulla ( cioè
può essere maggiore oppure minore di 1, variando da 0 a ¥. Per rifiutare
l'ipotesi nulla H0 alla probabilità a, il valore
calcolato del c2 con gdl - minore
del valore tabulato alla probabilità a/2 nella coda sinistra, cioè c2 < oppure - maggiore del
valore tabulato alla probabilità a/2 nella coda destra, cioè c2 >
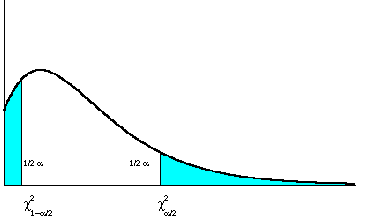
La figura successiva descrive l’asimmetria dei due valori critici, quando il chi quadrato ha pochi gdl. E’ una caratteristica che la distingue dalla distribuzione normale, che è sempre simmetrica intorno al valore medio. Inoltre è semplice
comprendere in quali estremi della distribuzione sono collocati
Nel test bilaterale, si rifiuta l’ipotesi nulla H0 quando il valore è troppo piccolo oppure troppo grande e pertanto cade nella parte colorata, detta zona di rifiuto o non accettazione.
Intervallo
atteso di c2(n-1) = per campioni estratti da una popolazione normale
Il test può essere anche a) unilaterale destro, b) unilaterale sinistro.
A) Il test è unilaterale
destro quando si intende verificare solamente se la varianza del campione è
statisticamente maggiore del valore con ipotesi H0: s2 £ s20 contro H1: s2 > s20
In questo caso, il risultato del test tende a essere elevato e per rifiutare l'ipotesi nulla alla probabilità a il valore calcolato del c2 con gdl n-1 deve essere - maggiore del valore
tabulato alla probabilità a nella coda destra, cioè c2 > (Deve cadere nella parte destra della distribuzione, ma con limite a, non più a/2)
B) Il test è unilaterale
sinistro quando si intende verificare solamente se la varianza del campione
è statisticamente minore del valore con ipotesi H0: s2 ³ s20 contro H1: s2 < s20
In questo caso, il risultato del test è basso e per rifiutare l'ipotesi nulla alla probabilità a il valore calcolato del c2 con gdl n-1 deve essere - minore del valore
tabulato alla probabilità a nella coda sinistra, cioè c2 < (Deve cadere nella parte sinistra della distribuzione, ma con limite 1- a, non più 1 - a/2)
ESEMPIO 1 (TEST BILATERALE). Con un numero molto alto di dati, ricavati da rilevazioni automatiche frequenti, è stata misurata la quantità di conservante in un alimento prodotto da una azienda; la sua varianza è s2 = 1,86. Sui prodotti di una azienda concorrente, sono stati analizzati sei campioni, con i risultati seguenti:
Le due varianze sono significativamente differenti alla probabilità a = 0.05?
Risposta. Per verificare l'ipotesi bilaterale H0: s2 = s20 = 1,86 contro H1: s2 ¹ s20 - si calcola la devianza del campione. Supponendo che i dati del campione siano stati estratti da una popolazione normale, con la formula abbreviata
si ottiene
una devianza uguale a 3,55 con 5 gdl. La sua varianza è
(Nella pratica, è del tutto inutile questo ultimo passaggio per calcolare la varianza, anche se l’ipotesi verte sulla varianza, in quanto dovrebbe poi essere moltiplicata per i gdl)
Il valore del c2
con 5 gdl risulta uguale a 1,91.
Per un test con a = 0.05 esso deve essere confrontato con i valori critici riportati nella tabella sinottica per gli stessi gdl (5) alla probabilità 1-a/2 e a/2 nelle due code: - alla probabilità a = 0.975 il valore critico è c2 = 0,831 - alla probabilità a = 0.025 il valore critico è c2 0 12,833 Il valore calcolato (1,91) è compreso nell'intervallo tra i due valori critici che definiscono i limiti di accettabilità. Di conseguenza, nell’ipotesi che H0 sia vera, ha una probabilità superiore al 5% di avvenire per caso. Non si può rifiutare l'ipotesi nulla. La varianza della seconda ditta non è significativamente differente da quella della prima, almeno con i 6 dati raccolti. E’ ovvio che all’aumentare del numero di osservazioni aumenta la potenza del test, vale a dire - la probabilità di
dimostrare che il valore calcolato
ESEMPIO 2 (TEST UNILATERALE). Se vi fosse stato motivo di credere, prima di raccogliere i dati e come può essere giustificato dall'uso di macchine più moderne, che il prodotto della seconda azienda abbia una varianza minore, il test sarebbe stato unilaterale. Le ipotesi sarebbero H0: s2 ³ s20 contro H1: s2 < s20
Poiché la varianza campionaria
è - se essa è significativamente minore - oppure ne può rappresentare una variazione casuale.
Il valore del c2
risulta uguale a 1,91 con 5 gdl. Deve essere confrontato con il valore critico alla probabilità a = 0,95. Nella tabella, tale valore critico risulta uguale a 1,145. E’ minore di quello calcolato (1,91) e pertanto non è possibile rifiutare l'ipotesi nulla.
Se l'ipotesi fosse stata di segno opposto, H0: s2 £ s20 contro H1: s2 > s20 ovviamente il
valore s2 calcolato avrebbe dovuto essere maggiore di quello (Controllare sulla tabella dei valori critici del c2.)
| |||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
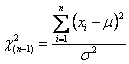 oppure
oppure