VERIFICA DELLE IPOTESITEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTAE TEST SULLA VARIANZA CON INTERVALLI DI CONFIDENZA
4.14. LA POTENZA A POSTERIORI E A PRIORI PER LA SIGNIFICATIVITA’ DELLA DIFFERENZA TRA UNA VARIANZA OSSERVATA E UNA VARIANZA ATTESA
Ricorrendo alla distribuzione c2 possono essere calcolate - la potenza a posteriori (1-b) e - la potenza a
priori ( dei test sulla
significatività della differenza tra una varianza campionaria
La potenza a
posteriori (1-b), cioè misurata dopo che gli - per un test bilaterale quindi con ipotesi H0: s2 = s20 contro H1: s2 ¹ s20 può essere ricavata mediante la relazione
- per un test unilaterale con ipotesi H0: s2 £ s20 contro H1: s2 > s20 con la relazione
- per un test unilaterale con ipotesi H0: s2 ³ s20 contro H1: s2 < s20 con la relazione
ESEMPIO 1 (TEST
UNILATERALE SULLA POTENZA). La varianza di un nuovo reagente è stata indicata
dall’azienda produttrice in Quale è la potenza del test, se con una significatività a = 0.05 si vuole dimostrare che la varianza vera del nuovo prodotto è effettivamente maggiore di quella indicata?
Risposta. E' un test unilaterale con ipotesi H0: s2 £ s20 contro H1: s2 > s20 La relazione
con e quindi
permette di
stimare un valore del Nella tavola sinottica dei valori critici con gdl 7, esso cade - tra il valore corrispondente alla probabilità a = 0.25 - e quello per la probabilità a = 0.5. I programmi
informatici di norma forniscono una stima più precisa della probabilità
corrispondente a tale valore del chi- quadrato, in quanto possono usare tabelle
molto più dettagliate o stimare direttamente la distribuzione delle
probabilità. Con un programma informatico, in questo caso è stato stimato che Una potenza 1-b = 0,36 può essere giudicata molto bassa. Infatti esiste solo il 36% di probabilità che tale esperimento, con i parametri in indicati, risulti significativo. Nella programmazione di un esperimento, di norma deve superare almeno 0.80 quando si pensa di utilizzare, sui dati raccolti, un test che si vorrebbe significativo alla probabilità a = 0.05.
Dopo uno studio
pilota che fornisce le informazioni di base oppure la lettura di una ricerca
pubblicata che si vuole ripetere, diventa logico chiedersi: “Quanti dati
occorre raccogliere, per realizzare un esperimento con il quale si possa
dimostrare, alla probabilità a e con un rischio b prestabiliti, che la varianza
reale Questa varianza può essere stimata - sia sui dati di un solo campione, come presentato nel paragrafo precedente, - sia su due campioni dipendenti.
Nella statistica applicata, spesso è richiesto che si analizzi la varianza di uno strumento utilizzato da persone differenti oppure di un reagente impiegato in condizioni differenti. Si supponga che su 10 campioni due tecnici conducano la stessa analisi, ottenendo i risultati nell'esempio successivo:
La procedura per calcolare la varianza delle risposte tra i due operatori illustrata nei 3 punti successivi: 1 – Dalle due serie
di dati Potrebbe anche essere le differenze di segno opposto rispetto a quelle indicate nella tabella, vale a dire:
Cambierebbe solamente il segno della loro media, non la varianza.
2 - Si calcola le
media Con i dati dell’esempio
si ottiene 3 – Infine si ricava la varianza
Con i dati dell’esempio
si ottiene Essa può essere confrontata con la varianza dichiarata, come illustrato nel paragrafo precedente.
La potenza a
priori, o stima delle dimensioni minime 1) alla probabilità a desiderata 2) con il rischio b prefissato,
- in test unilaterale con ipotesi H0: s2 £ s20 contro H1: s2 > s20 è ricavato da
- in un test unilaterale con ipotesi H0: s2 ³ s20 contro H1: s2 < s20 è ricavato da
operando in modo iterativo. (Per la stima di
I due valori del c2 richiesti dalla formula, - quello per la per la probabilità a - quello per il rischio b possono essere scelti nella tavola sinottica solo conoscendo i gdl. Ma essi dipendono
dal numero Si procede quindi per tentativi, fino a individuare i due valori critici che determinano il rapporto richiesto, cioè
I loro gdl
forniscono la stima del numero minimo (Individuare i valori da cui partire è determinato dall'esperienza. Coloro che affrontano questo procedimento per la prima volta ovviamente dovranno fare più tentativi per identificare il valore necessario).
ESEMPIO 2 (NUMERO
MINIMO DI DATI Quanti campioni deve analizzare, per dimostrare statisticamente che la varianza reale del reagente è effettivamente maggiore di quella indicata, con una significatività a = 0.05 e un rischio b = 0.10?
Risposta. Trattandosi di un test unilaterale con H0: s2 £ s20 contro H1: s2 > s20 si deve utilizzare la relazione
Tentativo I Con s2
= 2,69 visto il risultato
dell'esempio precedente che ha fornito una potenza particolarmente bassa con Dalla tabella dei
valori critici, con gdl = 34 ( - per la probabilità a = 0.05 il valore c2 = 48,602 - per la probabilità 1-b = 0.90 il valore c2 = 23,952 (nella tabella vedere probabilità 0.90) Dai rapporti delle due formule precedenti risulta (1)
cioè che - il rapporto
(0,493) tra i due valori critici del - è sensibilmente inferiore a quello delle due varianze (0,558). Questa prima scelta
di
Tentativo II Di conseguenza,
poiché il rapporto tra questi due Può apparire
ragionevole tentare con (Solamente l'esperienza porterà a scelte che si dimostreranno vicine al valore corretto).
Dalla tabella dei
valori critici, con gdl = 54 ( - per la probabilità a = 0.05 il valore c2 = 72,153 - per la probabilità 1-b = 0.90 il valore c2 = 41,183 (nella tabella vedere probabilità 0.90)
Dal rapporto tra i due valori critici
(1)
si ottiene un risultato (0,571) che questa volta è maggiore di quello tra le due varianze (0,558), rimasto ovviamente immutato . Ma questa volta la differenza è piccola, come possono evidenziare i risultati dei due rapporti, arrotondati alla seconda cifra decimale (0,57 contro 0,56).
Tentativo III Con un terzo
tentativo, questa volta si deve provare con un numero leggermente minore, che
indicativamente può essere Dalla tabella dei
valori critici con gdl = 49 ( - per la probabilità a = 0.05 il valore c2 = 66,339 - per la probabilità 1-b = 0.90 il valore c2 = 36,818 (nella tabella vedere probabilità 0.90)
Dal rapporto tra i due valori critici
(1)
si ottiene (0,555). Questa volta il
risultato del rapporto tra i due Poiché rapporto tra
i due Con interpolazione
anche grossolana rispetto agli ultimi due valori, come risposta conclusiva è
possibile indicare non in 50 ma in 51-52 dati il numero minimo
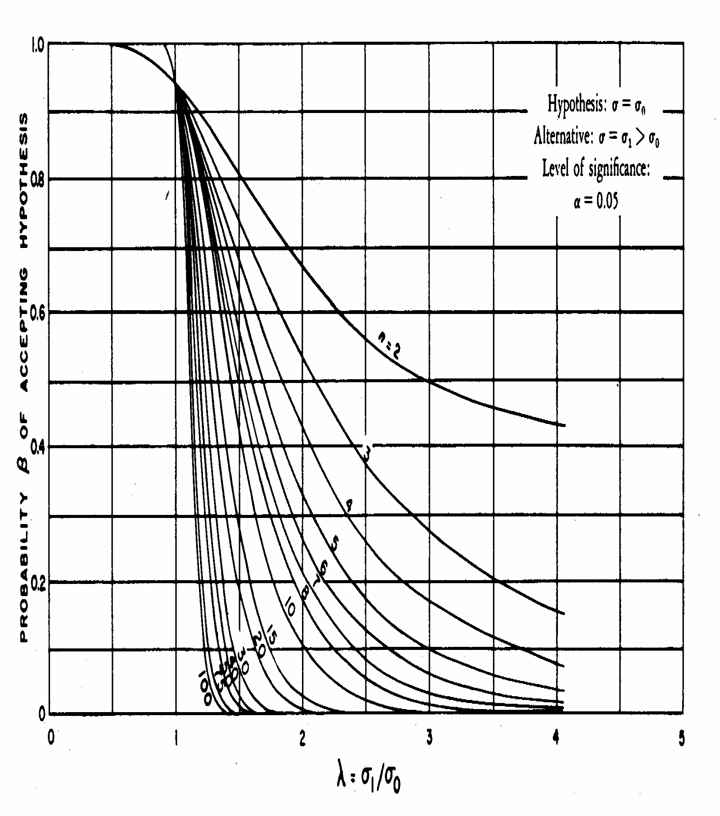
Con metodi grafici proposti negli anni 40 e 50, del tutto analoghi a quelli utilizzati per la media, è possibile ottenere gli stessi risultati, - in modo molto più rapido, - seppure più impreciso, ma spesso
ugualmente utile per una prima stima del rischio b e del numero
minimo Il grafico riportato nelle pagine seguenti, è stato proposto nel 1946 da C. D. Ferris, F. E. Grubbs e L. C. Weaver con l’articolo Operating Characteristics for the Common Statistical Tests of Significance (pubblicato su Annals of Mathematical Statistics Vol. 17, p. 181) e è stato divulgato in particolare dal manuale del dipartimento di ricerca della Marina militare Americana, pubblicato nel 1960, Statistical Manual (con autori Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, è stato pubblicato da Research Department U. S: Naval Ordnance Test Station, Dover Publications, Inc., New York, XVII + 288 p.), E’ solamente una dimostrazione e ha applicazioni limitate, in quanto è utile - solamente per il caso di un test unilaterale, presentato nel manuale con la simbologia H0: - e solamente per la probabilità a = 0.05. Dopo aver calcolato il parametro l attraverso la relazione
dove - (nella figura
successiva è indicato con - permette di stimare a) - il rischio b, b) - il numero
minimo
- trasferito orizzontalmente sull’asse delle ordinate, esso indica il rischio b. B - Per stimare
le dimensioni minime ( - dopo aver individuato il valore di l sull’asse delle ascisse si sale verticalmente - e dopo aver prefissato il valore di b ci si sposta in modo orizzontale: Per l’ipotesi
nell’altra direzione H0:
ESEMPIO 3 (STIMA
DI b CON IL GRAFICO E
GLI STESSI DATI DELL’ESEMPIO 1). La varianza nelle risposte di un reagente è
stata indicata dall’azienda produttrice in Quale è la
potenza (
Risposta. Con l’indice l
Individuato sull’asse delle ascisse, il valore l = 1,34 - proiettato
verticalmente incontra la curva teorica di - che, trasferito orizzontalmente sull’asse delle ordinate, indica approssimativamente b = 0,65. La potenza Per la rapidità della risposta e la semplicità d’uso, è comprensibile la diffusione di questi grafici in analisi di routine. Resta il problema che, pure fornendo una risposta corretta, attraverso essa il tecnico raramente può comprendere esattamente quali sono i parametri che ha effettivamente utilizzato in questa determinazione.
ESEMPIO 4 (STIMA
DI Quanti campioni deve analizzare per dimostrare statisticamente che la varianza reale del reagente è effettivamente maggiore di quella indicata, con una significatività a = 0.05 e un rischio b = 0.10?
Risposta.
Trattandosi di un test unilaterale con l’indice l
Individuato, sull’asse delle ascisse, il valore l = 1,34 - si deve salire verticalmente; -
contemporaneamente sull’asse delle ordinate si deve prendere il valore - queste due rette si incontrano in un
punto, che cade approssimativamente sulla curva Serve un campione di circa 50 dati. Dal confronto tra i risultati dei 4 esempi sviluppati, emerge
con evidenza che, soprattutto per campioni grandi, quando si utilizzano i grafici
si ottengono stime puramente indicative della dimensione
| |||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
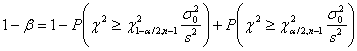
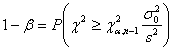
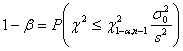 oppure
oppure 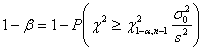
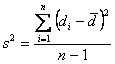
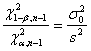
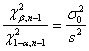
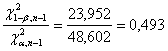 e (2)
e (2) 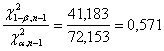 e
(2)
e
(2) 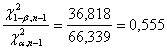 e (2)
e (2)