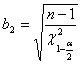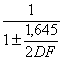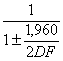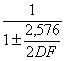VERIFICA DELLE IPOTESITEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTAE TEST SULLA VARIANZA CON INTERVALLI DI CONFIDENZA
4.16. INTERVALLO DI CONFIDENZA DELLA DEVIAZIONE STANDARD E STIMA DELLA DIMENSIONE DEL CAMPIONE
Nel paragrafo
precedente, è stata presentata la serie di passaggi logici che dimostrano come i
valori estremi dell'intervallo di confidenza della deviazione standard (
in modo del tutto analogo al metodo presentato per la varianza
ESEMPIO 1. Su 20
campioni di un farmaco, è stata misurata la quantità di principio attivo: la
deviazione standard è risultata
Risposta. Per
utilizzare la formula appena riportata, con - per a = 0.975 il valore
è - per a = 0.025 il valore è Con essi, - il limite inferiore (lower limit)
risulta L1 = 8,13 - il limite superiore (upper limit)
risulta L2 = 15,63.
In molte aziende,
queste misure dell’intervallo di confidenza della deviazione standard The following method is preferable in practice.
COEFFICIENTI PER DETERMINARE I LIMITI DELL’INTERVALLO DI CONFIDENZA DELLA DEVIAZIONE STANDARD s
Per la probabilità a prestabilita e per i gradi di libertà (DF) del campione, - il limite
inferiore è L1 = - il limite
superiore è L2 = dove Essi possono essere ricavati facilmente da
Ad esempio, con
gradi di libertà (DF) = - per a = 0.975 il valore
- per a = 0.025 il valore Nella tabella sono
riportati i coefficienti
con arrotondamento.
Per campioni
grandi (DF >100), sempre secondo quanto riportato nello stesso manuale,
i valori - per
- per
- per
ESEMPIO 2 (CON
GLI STESSI DATI DELL’ESEMPIO 1). Su 20 campioni di un farmaco, è stata misurata
la quantità di principio attivo: la deviazione standard è risultata Quale è il limite
di confidenza della deviazione standard vera
Risposta. Per Di conseguenza, con
- il limite
inferiore è L1 = - il limite
superiore è L2 =
Il calcolo dell’intervallo di confidenza della deviazione standard non comporta alcun vantaggio, né teorico né pratico, rispetto al calcolo equivalente effettuato con la varianza. L’uso della deviazione standard diventa utile, - quando attraverso
i metodi grafici si voglia determinare la dimensione - per stimare
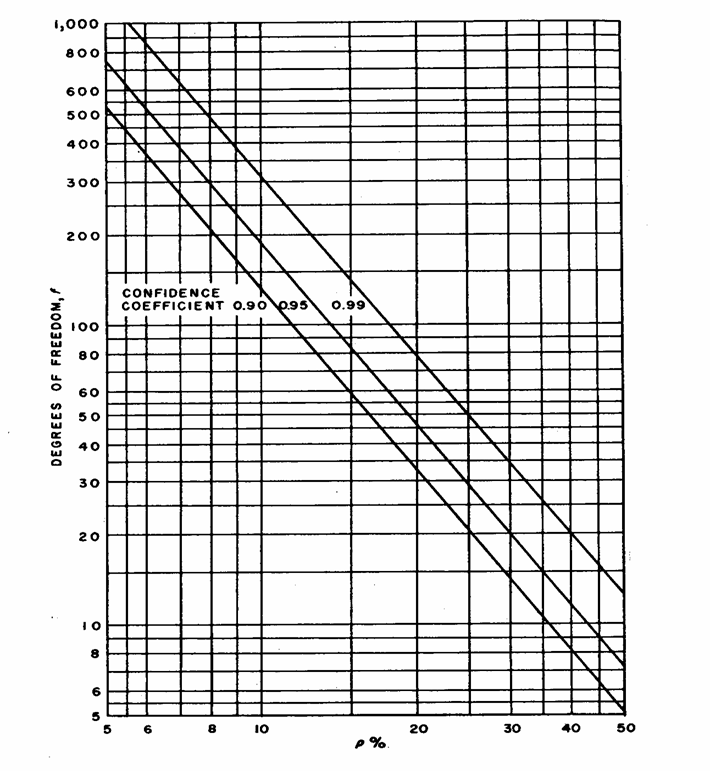
ESEMPIO 3 (USO DEL
GRAFICO PER STIMARE - si vuole
ottenere una deviazione standard - abbia una
probabilità P del 95% di contenere il valore vero
Risposta. Sull’asse delle ascisse, - si individua il
valore - fino a incontrare la retta del coefficiente di confidenza 0,95 in un punto - che trasferito orizzontalmente sull’asse delle ordinate corrisponde ai gradi di libertà 20-21. Servono almeno
21-22 misure, per calcolare un valore
Il grafico precedente è una modifica, fatta dagli autori del testo della marina militare americana, del metodo proposto da Greenwood J. A. e M. M. Sandmire nel 1950 nell’articolo Sample Size Required for Estimating tre Standard Deviation as a Percent of Its True Value (su Journal of the American Statistical Association Vol. 45, p. 258), allo scopo di renderne l’uso ancora più semplice e rapido.
ESEMPIO 4 (USO DEL
GRAFICO PER STIMARE - si vuole ottenere
una deviazione standard - abbia una
probabilità P del 95% di contenere il valore vero
Risposta. Sull’asse delle ascisse, - si individua il
valore - fino a incontrare la retta del coefficiente di confidenza 0,95 in un punto - che, trasferito orizzontalmente sull’asse delle ordinate, corrisponde a gradi di libertà 190. Servono almeno 190 misure Nella lettura del numero di gradi di libertà sull’asse delle ordinate, occorre porre attenzione al fatto che la scala è di tipo logaritmico e quindi per valori maggiori dei gradi di libertà l’errore nell’approssimazione diventa molto più grande, in frequenze assolute
Il numero Più esattamente, - tra il valore - si mantengono le
relazioni quadratiche, già illustrate per la differenza A dimostrazione di questa relazione, nel confronto tra i risultati degli ultimi due esempi (3 e 4) è semplice osservare che - nell’esempio 4
l’errore massimo che si vuole commettere - e che il numero
minimo
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
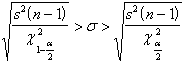
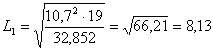
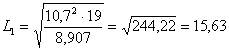
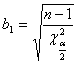 e
e