VERIFICA DELLE IPOTESITEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTAE TEST SULLA VARIANZA CON INTERVALLI DI CONFIDENZA
4.18. POTENZA A PRIORI E A POSTERIORI DEL TEST F PER L’UGUAGLIANZA DI DUE VARIANZE
Il test F
- con gdl = 8 al numeratore e gdl = 5 al denominatore non permette di dimostrare che la varianza al numeratore (20,55) è statisticamente maggiore di quella al denominatore (8,66). Il test non è significativo, poiché il valore critico per a = 0.05 è F = 4,82. Spesso è importante
sapere quanti dati ( - il test risulti significativo alla probabilità a prefissata, - e con il rischio b prestabilito. Per rispondere a questa domanda sono possibili due metodologie: a) metodi grafici, b) calcoli fondati su distribuzioni teoriche. Sono presentati esempi di entrambe le metodologie, benché un loro uso sicuro richieda una trattazione ancor più approfondita e una dotazione più ricca di tabelle e grafici, che possono essere fornite solamente da testi specifici.
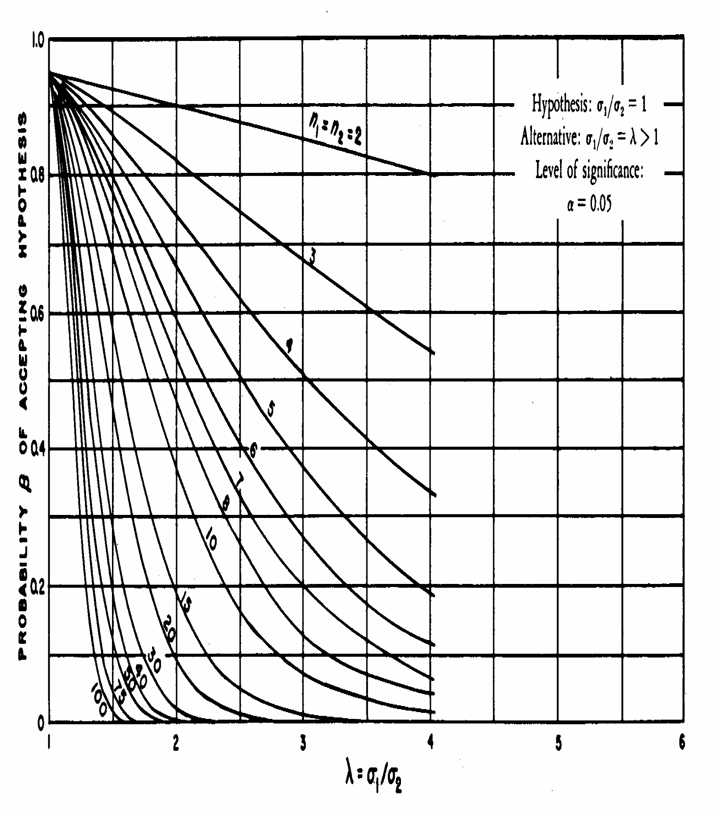
A) Il grafico riportato nella pagina successiva è stato proposto nel 1946 da C. D. Ferris, F. E. Grubbs e L. C. Weaver con l’articolo Operating Characteristics for the Common Statistical Tests of Significance (pubblicato su Annals of Mathematical Statistics Vol. 17, p. 181). Nelle applicazioni industriali della statistica è stato divulgato in particolare dal manuale del Dipartimento di Ricerca della Marina Militare Americana, pubblicato nel 1960, Statistical Manual (con autori Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, edito da Research Department U. S: Naval Ordnance Test Station, Dover Publications, Inc., New York, XVII + 288 p.).
L'uso del grafico è semplice. Benché l’ipotesi possa essere fatta sulle varianze, è necessario partire dal calcolo del rapporto tra le due deviazioni standard. Utilizzando quelle dell’ultimo esempio, dove
in cui ora la simbologia - per il numeratore
è si ricava
il rapporto l = 1,54 (deve sempre essere maggiore di 1, come ovvio per il tipo di test).
Solamente per la probabilità a = 0.05 - dopo aver prefissato il rischio b che, ad esempio, potrebbe essere b = 0.2 letto sulle ordinate, - sull’asse delle ascisse si cerca il punto corrispondente a l = 1,54. - Il loro punto di
incontro approssimativamente cade tra la curva di Si può concludere che servono due campioni, formato ognuno da circa 35 osservazioni.
Se, - mantenendo costanti la probabilità a = 0.05 e l = 1,54 - il rischio scelto fosse stato b = 0.1, - si sarebbe giunti
alla conclusione che approssimativamente servono
Sempre con l’uso
del grafico è possibile stimare il rischio b o la potenza - conoscendo a e l - e dopo aver
scelto Ad esempio, sempre a = 0.05 e l = 1,54 - supponendo che le
due deviazioni standard siano state calcolate da due campioni bilanciati,
formati ognuno da - nel grafico si
può osservare che la perpendicolare di l = 1,54 incontra la curva - in un punto che sull’asse delle ordinate corrisponde a b = 0.73. In questo test, il rischio che il rapporto non risultasse significativo era appunto del 73%. La potenza del test
(
B) I metodi fondati su distribuzioni teoriche sono numerosi, tutti relativamente complessi in funzione del livello di approssimazione accettato e della forma delle distribuzioni di probabilità assunte come modello dio riferimento. Anche quando si ricorre all’uso del test F cioè al rapporto tra - la varianza
maggiore ( F = per verificare l’ipotesi di omoschedasticità tra due gruppi (A e B), quindi per testare l’ipotesi nulla H0: contro l’ipotesi alternativa bilaterale H1: è possibile chiedersi: “Quanti dati servono affinché l’ipotesi nulla possa essere respinta alla probabilità a, con una probabilità b di commettere un errore di II Tipo?” E’ la stima della
potenza
Secondo quanto riportato nel testo di M. M. Desu e D. Raghavarao del 1990 (Sample Size Methodology, Academic Press, Boston, Massachussetts, 135 pp.) e ripreso da Jerrold H. Zar nel testo del 1999 Biostatistical Analysis (fourth edition, Prentice Hall, Upper Saddle River, New Jersey), è possibile utilizzare l’approssimazione alla distribuzione normale, valida per grandi campioni. In ognuno dei due
campioni il numero minimo
dove - - - - -
Volendo utilizzare il logaritmo a base 10 (log), al posto del precedente logaritmo naturale (ln), l’equazione diventa
Nel caso (più raro nella ricerca ambientale e biologica) in cui si voglia, con un test unilaterale, dimostrare che la varianza di un gruppo di osservazioni è maggiore di quella dell’altro gruppo, per cui l’ipotesi alternativa H1 è nelle formule precedenti - la varianza ipotizzata come maggiore, che deve risultare effettivamente tale, va posta al numeratore, - Come già rilevato in precedenza nell’analisi della omoschedasticità con un test unilaterale, questo test ha significato solo se il rapporto tra le due varianze a confronto risulta maggiore di 1.
Il valore In alcune condizioni, per il diverso costo delle osservazioni nei due gruppi, si può pensare che i gdl di un gruppo (nA) siano m volte maggiori dei gdl dell’altro gruppo (nB). Secondo i due testi citati in precedenza,
Avendo ricavato si ricava prima
e da esso
La stima di Spesso, soprattutto
quando un test non risulta significativo, è utile chiedersi quale era la
probabilità che esso potesse risultarlo: è la potenza a posteriori o,
più semplicemente, la potenza del test (
Se due campioni hanno
lo stesso numero di dati ( - usando il
logaritmo naturale ( Zb = - usando il
logaritmo a base 10 ( Zb = dove - Za deve essere preso in una distribuzione bilaterale oppure unilaterale, in rapporto a quanto esplicitato nell’ipotesi H1 (se un test a due code o a una coda).
Se due campioni
hanno un numero differente di dati ( Dopo aver stimato
dove - - nelle formule precedenti al posto di
si introduce dove - Di conseguenza, il valore di Zb (sempre in una distribuzione unilaterale) - usando il
logaritmo naturale (
Zb =
- usando il
logaritmo a base 10 ( Zb = dove - Za deve essere preso in una distribuzione bilaterale oppure unilaterale, in rapporto a quanto esplicitato nell’ipotesi H1
ESEMPIO 1. Per applicare un test parametrico sul confronto tra due medie per due campioni indipendenti, si richiede l’omoschedasticità della varianza. In uno studio preliminare, sui campione A e B si sono ottenuti i seguenti risultati
con i quali F (12,11)
=
non era stata rifiutata l’ipotesi nulla H0: - poiché il loro rapporto F è uguale a 2,093 - mentre il valore critico di F(12,11) per il livello di probabilità a = 0.05 è 2,79.
Calcolare a) Quanti dati ( - alla probabilità a = 0.05 - con un rischio d’errore di II tipo (b) = 0.10 (o una potenza 1-b = 0.90)?
b) Quale è la
potenza (
Risposte A) E’ un test bilaterale, in cui - per a = 0.05 in una distribuzione bilaterale il valore di Z è 1,96 - per b = 0.10 in una distribuzione unilaterale il valore di Z è 1,28 con
si ottiene
un numero minimo Anche con questa dimostrazione si mostra quanto fosse errato, in un esempio precedente con un campione piccolo, arrivare alla conclusione che le due varianze erano simili, semplicemente perché non era stata rifiutata l’ipotesi nulla alla probabilità del 5%. Sarebbe stato sufficiente raddoppiare il numero di osservazioni (passare rispettivamente da 12 e 13 dati nei due gruppi a 22 per ognuno) per giungere alla conclusione che le due varianze sono significativamente differenti, con una probabilità del 90 per cento.
B) Con due campioni sbilanciati, in cui i dati della varianza al numeratore sono 13 e quelli della varianza al denominatore sono 12,
si ricava e che il valore di Zb Zb= con - il valore di Za, alla probabilità a = 0.05 in una distribuzione bilaterale, uguale a 1,96 - risulta Zb =
Zb = uguale a 0,425. In una distribuzione unilaterale, ad esso corrisponde un valore di probabilità collocato tra 0,337 e 0,334. In conclusione, - la probabilità - e quindi la
potenza del test
| ||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |

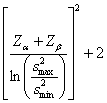
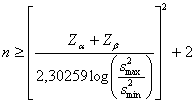
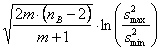 - Z
- Z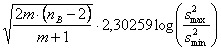 - Z
- Z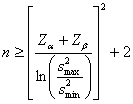
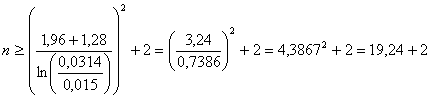 = 21,24
= 21,24