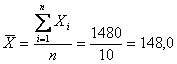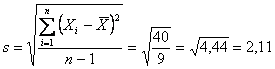VERIFICA DELLE IPOTESI

TEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTA

E TEST SULLA VARIANZA

CON INTERVALLI DI CONFIDENZA

 

 

 

 

4.23.   PRECISIONE E ACCURATEZZA DI UNO STRUMENTO O DI UNA ANALISI

Quando con uno strumento si rileva una misura (il dato), l’informazione raccolta è formata da due componenti, che si sommano:

-  una è sistematica, uguale per tutti,

-  l’altra, chiamata errore, non è spiegata e varia tutte le volte in modo imprevisto.

Ad esempio, nella serie di 10 misure riportate nella prima riga (,

 -  ogni dato può essere visto come la media del gruppo (), uguale per tutti, più o meno una quantità () ignota e diversa tutte le volte:

 

 

 

 

La parte costante deve avere la caratteristica di essere vicina al valore vero e di avvicinarsi ad esso sempre di più, all’aumentare del numero di dati raccolti.

Ma nella analisi statistica sono molto importanti soprattutto gli errori, la parte variabile. Questi errori devono avere caratteristiche precise, affinché

-  la parte costante possa essere stimata senza distorsioni,

-  i test che vengono applicati forniscano risultati attendibili.

Essi devono

-  essere distribuiti in modo casuale intorno allo zero: non è corretto che seguano una legge costante, come un alternarsi regolare oppure che la i primi siano tutti positivi e gli ultimi tutti negativi;

- devono essere distribuiti in modo normale, intorno allo zero: non è corretto che vi siano molti valori piccoli e pochi o uno solo molto grandi.

Se nei dati esistono queste caratteristiche che li rendono non adatti all’analisi, come la distribuzione non casuale, significa che nell’esperimento è stato commesso un errore sistematico o periodico, per cui i dati non sono attendibili. Rimane solamente la ripetizione dell’esperimento, per effettuare una raccolta di dati che sia corretta.

 

Se la distribuzione degli errori non è normale, con le trasformazioni si cercherà di renderla normale, come è descritto in un capitolo successivo dopo l'analisi della varianza.

Oltre a questi errori casuali, nei dati possono essere presenti valori molto diversi da tutti gli altri, con un errore molto grande. Si chiamano in italiano valori anomali, in inglese gross errors o più frequentemente outliers, un termine che ora si usa anche in italiano. E’ evidente che uno solo di essi determina la stima di una media, la parte costante per tutti, che è più alta del reale. Inoltre, poiché gli scarti dalla media hanno sempre un totale uguale a zero, i molti errori piccoli avranno tutti lo stesso segno e l’errore grande avrà il segno opposto. In un capitolo successivo è descritto come individuarli e quali analisi statistiche applicare, quando essi sono presenti.

 

 

 

Queste caratteristiche dei dati sono definite, con un linguaggio più tecnico, dalle proprietà che devono avere le misure.

Le due proprietà illustrate per gli stimatori, la precisione e l’accuratezza, sono caratteristiche che spesso sono riferite anche agli strumenti di misura, a un reagente, ai risultati di una analisi chimica o biologica.

Estensivamente, accuratezza e precisione sono quindi riferite anche alle misure ottenute.

La sovrapposizione di concetti già illustrati per gli stimatori è tale che le differenti situazioni possono essere illustrate con le stesse figure.

 

La stima di accuratezza o meglio della inaccuratezza è fondata sulla

- distanza tra la media campionaria  e la media reale m

 

La stima della precisione  o meglio della imprecisione è fondata sulla deviazione standard, concettualmente sulla

- distanza tra le singole misure  e la loro media

 

Si supponga di avere un campione di sale sciolto in un diluente. Poiché sono stati sciolti 150 mg di sale in un dl di diluente, la concentrazione vera è nota: esattamente m = 60 mg/dl.

Per valutare l’accuratezza di uno strumento per l’analisi automatica, di questo campione sono effettuate 10 titolazioni, con approssimate al mg.

Sono stati ottenuti i risultati seguenti:

 

 

Fornire la stima della inaccuratezza e della imprecisione.

 

Risposta. Si calcola prima la inaccuratezza, in quanto è fondata sulla media campionaria  delle  analisi. Si ottiene

 

Con media campionaria  = 148 è stato commesso un errore nella titolazione, poiché sappiamo (avendo preparato la soluzione in modo corretto) che la quantità reale è m = 150 mg. 

La inaccuratezza dello strumento è = 140 - 150 = 2 mg/dl

La misura può essere espressa come percentuale dell’errore, rispetto al valore reale.

Con i dati dell’esempio, è 1,33%.

 

L’imprecisione è determinata dalla variabilità delle misure, dalla differenza di ogni dato rispetto alla media del campione,

-  misurata come deviazione standard  oppure  come coefficiente di variazione.

Da

 

 

 si ricava che l’imprecisione dello strumento

 è

 

  e quindi ha una deviazione standard  = 2,11 mg/dl

 che può essere espressa anche

 come

 

 coefficiente di variazione  con il risultatoseguente:  CV = 1,41% del valore medio vero.