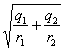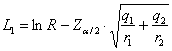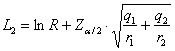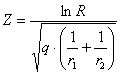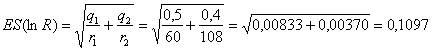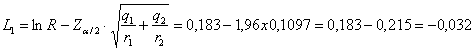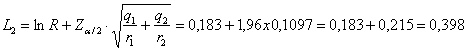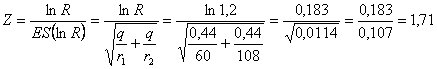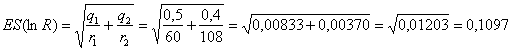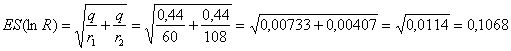PROPORZIONI  E  PERCENTUALI,  RISCHI,  ODDS  E  TASSI

 

 

 

5.15.  IL RAPPORTO TRA DUE PROPORZIONI (R): INTERVALLO DI CONFIDENZA E SIGNIFICATIVITA’; FORMULA TEST-BASED DI MIETTINEN PER R.

 

 

Vari concetti illustrati in questo capitolo sono presentati anche in altri. La differenza tra due proporzioni, trattata nei paragrafi precedenti, è già stata esposta nel capitolo sul chi-quadrato; il rapporto tra due proporzioni e tra due odds, discusso in questo paragrafo, è riproposto nel capitolo sulle misure di associazione. Non si tratta di una banale duplicazione.

Anche quando i concetti sono identici e i metodi sono sovrapponibili, l'approccio è differente. Il confronto tra essi serve per conseguire una visione più ampia del problema, che è didatticamente utile per evidenziare le differenze tra scuole e apprendere come giustificare, in modo più completo, la scelta di un test o di una variante nelle formule, tra i vari che sono stati proposti in 50 anni di sviluppo della metodologia. Anche i pacchetti informatici, presenti su un mercato sempre più ampio ed esigente, quando propongono gli stessi test spesso si rifanno a metodi o formule differenti. In conclusione, conoscere approcci diversi è utile per raggiungere quella cultura statistica che permette di giustificare le differenze tra metodi. Serve, nella presentazione di un rapporto scientifico o una di pubblicazione, anche per controbattere quelle chiusure ideologiche, non insolite nei referee di questa disciplina, che accettano come valida solamente una impostazione statistica. E spesso senza motivazioni, senza giudizi sulla potenza o sulla robustezza del test, sul tipo di scala oppure sulle caratteristiche della distribuzione dei dati, sul rischio a oppure sulle dimensioni del campione.

In questo settore della statistica, le differenze fondamentali tra i test derivano dall’essere fondati su probabilità esatte o asintotiche, dal fatto che le soluzioni siano più o meno approssimate, dal richiedere metodi lunghi e difficili oppure fondati su soluzioni rapide.

 

Un primo aspetto della ricerca è quasi sempre l’uso di un linguaggio scientifico. Nella ricerca epidemiologica e ambientale, sovente si usano termini equivoci.

Ad esempio, se la proporzione di persone che soffrono di allergia in un determinato periodo è del 30% (p₁ = 0,30) e si afferma che nei 10 anni successivi hanno avuto un aumento del 15%, si intende dire che:

1 -  sono diventati il 45% (p₂ = p₁ + d = 0,30 + 0,15 = 0,45)?

Oppure che

2 - sono diventati il 34,5% (p₂ = p₁ x R = 0,30 x 1,15 = 0,345)?

 

Nel primo caso, per confrontare il valore finale con quello iniziale, è stata utilizzata la differenza tra due proporzioni:

Nel secondo, il rapporto tra due proporzioni:

 

Da questa osservazione, derivano due conseguenze.

-  La prima è banale: per evitare fraintendimenti, è utile riportare tre informazioni, in particolare le prime due: (a) il valore iniziale, (b) il valore finale, (c) il valore dell'accrescimento, che può essere la differenza oppure il rapporto; ma, insieme con i primi due, è sempre comprensibile senza equivoci.

-  La seconda è un problema tecnico: come si analizza un rapporto tra due proporzioni e come si confrontano due rapporti, dopo che nei paragrafi precedenti sono state presentate le tecniche per l'analisi di una differenza tra proporzioni.

 

Collegato al concetto di rapporto tra due proporzioni nei testi di statistica applicata spesso è presente anche il concetto del rapporto tra due odds.

Sono differenti, ma quando un fenomeno è raro, quindi le proporzioni sono basse, i risultati dei due metodi sono simili. Ne consegue che in letteratura è facile vedere l’utilizzo di uno al posto dell’altro, inducendo le persone con poca esperienza tecnica a credere che essi siano uguali, una semplice variante matematica come la formula abbreviata e la formula euristica che sono stati presentati per alcuni test.

Il rapporto tra due odds (odds ratio), che a prima vista appare meno semplice, in alcune analisi statistiche offre il vantaggio tecnico non trascurabile di permettere l'uso della regressione logistica. E’ un metodo importante nella interpretazione statistica degli studi caso-controllo, frequenti in medicina, farmacologia ed ecotossicologia.

Utilizzando la simbologia riportata schematicamente nella tabella successiva

 

 

 è evidente

- sia la differenza tra una proporzione       e    un odds  ,

- sia il significato delle due proporzioni   e   

e quindi quello del rapporto tra esse

 

Quando due proporzioni sono uguali, il rapporto è  = 1

Ma se , il rapporto  tende a 0;

 mentre se , il rapporto  tende all’infinito positivo.

Ne deriva che la distribuzione di  ha una forte asimmetria destra.

Approssimativamente, è una distribuzione log-Normale, come dimostrano i dati successivi.

 

 

 

 

Con due proporzioni misurate in due campioni indipendenti,

1  - R può assumere valori come quelli riportati nella prima riga: i rapporti tra  e  variano in modo bilanciato;

 

2  - ma se si calcolano i rapporti, come nella seconda riga, e con essi si costruisce una distribuzione in classi di frequenza con passo 1, è semplice dedurre che tutti i rapporti minori di 1 saranno nella prima classe e gli altri formeranno 32 classi, con molte di esse vuote; risulta visivamente evidente che i valori R determinano una distribuzione con forte asimmetria destra.

 

3 – Infine, applicando a questa ultima distribuzione di dati la trasformazione logaritmica, in questo caso la log normale () come nella terza riga, si ottiene una distribuzione simmetrica, approssimativamente normale.

 

Con , si indica un rapporto campionario tra due proporzioni; il rapporto reale, quello della popolazione, è indicato con il simbolo greco r (rho minuscolo, anche se il precedente è maiuscolo).

 

Dopo la trasformazione di R in R, è possibile utilizzare la distribuzione normale ridotta Z,

- sia per costruire l’intervallo di confidenza di r,

- sia per confrontare due .

 

Nel primo caso, per stimare l’intervallo di confidenza di r a partire da un valore campionario , serve la varianza di .

Dato che

 e poiché le due proporzioni  e  sono indipendenti

 si ricava che

-  la varianza della differenza tra due proporzioni è uguale alla somma delle loro varianze.

 

Questo concetto è facilmente comprensibile con una dimostrazione elementare.

Se è vera l’ipotesi nulla H₀, le due proporzioni reali sono uguali ().

Quindi le proporzioni campionarie  e   possono avere variazioni casuali di entità simile, che

- a volte saranno nella stessa direzione  e  oppure   e , con il risultato che i loro effetti nella differenza si annullano () – () = 0  e  () – () = 0

-  altre volte saranno nella direzione opposta come  e , con il risultato che i loro effetti si sommano () – () =  in modo positivo o negativo () – () = .

Nello stesso modo della differenza tra due medie, questi ultimi due passaggi dimostrano che

-  la varianza di una differenza è uguale alla somma delle due varianze.

 

In conclusione,

1 - per la proporzione

la varianza stimata di  è uguale a   scritto anche  oppure

 

2 – per il  la varianza stimata diventa

 e con la radice quadrata

 =

 diventa l’errore standard (ES) di .

 

Da questa stima dell’errore standard,  si ricava che per la probabilità a,

A)   i limiti dell’intervallo di confidenza di  sono

-  il limite inferiore

-  il limite superiore

 

B)   i limiti dell’intervallo di confidenza di r (quindi del valore ) sono

 1 - il limite inferiore:  scritto anche ,

 2 - il limite superiore:  scritto anche ;

 

C)   la significatività del rapporto R è determinata

 mediante

 

Questa ultima formula dell’errore standard, che

-  richiede l’uso di  al posto di  e  presenti nella formula già indicata per l’intervallo di confidenza,

-   deriva dal fatto che l’ipotesi nulla che si intende verificare è

H₀:

-  nella quale la stima migliore di  è fornita da

 

- quando si  utilizzano i dati di due campioni indipendenti e dove .

Il test per la significatività del rapporto R spesso è scritto

 come

 

 evidenziando ancor meglio il suo errore standard dipende dal valore medio ponderato di .

 

ESEMPIO 1. (RAPPORTO R E SUOI LIMITI DI CONFIDENZA)   Dalle due proporzioni  e  ricavate da due campioni indipendenti, dove   = 108/180  e  = 60/120,

- calcolare il rapporto  e i limiti dell’intervallo di confidenza alla probabilità a = 0.05.

 

Risposta. Dopo aver calcolato  = 60/120 = 0,5   e    = 108/180 = 0,6

1 - si ottiene il rapporto .

 

Ma per avere, almeno approssimativamente, una distribuzione normale delle risposte campionarie possibili e quindi poter calcolare l’intervallo di confidenza mediante la distribuzione Z,

2 - tale rapporto deve essere trasformato in

3 - il cui errore standard (ES di ) con

 

 

    e 

 è

 uguale a 0,1097.

 

Poiché per a = 0.05 in una distribuzione normale ridotta bilaterale è riportato  Z = 1,96

4 – per l’intervallo di confidenza di 

-  il limite inferiore

 è  L₁ = -0,032

-  il limite superiore

 è  L₂ = 0,398.

 con probabilità del 95% che quanto affermato sia vero.

5 -  Infine, dall’intervallo di confidenza di  si ritorna all’intervallo di confidenza di .

Quindi, con i dati dell’esempio, intorno al valore medio campionario  si hanno

-  il limite inferiore  =

-  il limite superiore = .

In conclusione i limiti dell’intervallo fiduciale di r sono 0,969 e 1,489.

Ovviamente, con la trasformazione da  al rapporto R, l’intervallo non è più simmetrico.

 

ESEMPIO 2  (SIGNIFICATIVITA’ DEL RAPPORTO R CON DATI ESEMPIO 1).   Valutare la significatività del rapporto tra le due proporzioni  e  ricavate da due campioni indipendenti, dove   = 108/180  e  = 60/120.

 

Risposta. In un test bilaterale con

H₀:      contro      H₁:

 e dove

-   = 60     e       = 108

-   = 120     e       = 180

 dopo aver calcolato

-   = 60/120 = 0,5     e      = 108/180 = 0,6    

-   =

 

- 

 il rapporto R è

 

 e la sua significatività è verificata

 con

 

 ottenendo Z = 1,71.

In una distribuzione normale ridotta bilaterale, corrisponde alla probabilità P = 0,087.

Quindi non permette di rifiutare l’ipotesi nulla se, come prassi, la soglia di significatività minima è stata indicata in a = 0.05.

 

Come tutti gli intervalli di confidenza, pure quello precedente dovrebbe servire anche per valutare

 la significatività del rapporto

 in un test bilaterale con ipotesi

H₀:      contro      H₁:

In questi test, si rifiuta l’ipotesi nulla H_0,

-  quando nell’intervallo di confidenza di  non è compreso il valore 1 (che si dovrebbe ottenere quando l’ipotesi nulla è vera).

 

Di norma, l’intervallo di confidenza calcolato con la distribuzione normale ridotta Z e il test Z forniscono risposte identiche. Ma non nel caso del rapporto R e del test per la significatività di R, a motivo delle diverse formule utilizzate per calcolare l’errore standard di .

Esistono differenze; ma quasi sempre sono molto piccole, quando i campioni hanno dimensioni non troppo diverse. In pratica, anche per il rapporto R l’intervallo di confidenza è utilizzato per l’inferenza sulla sua significatività. La dimostrazione dell’esistenza di differenze trascurabili è data dalle due conclusioni precedenti, qui riportate:

 

A)  Nell’esempio 1 del paragrafo precedente, con   che varia tra

- il limite inferiore L₁ = 0,969

- il limite superiore L₂ = 1,489

-  il valore  = 1,0 è compreso nell’intervallo e quindi l’ipotesi nulla non è stata rifiutata, sempre con probabilità  a = 0.05 di un errore di Tipo I e in un test bilaterale.

 

B)  Per verificare la stessa ipotesi

H₀:      contro      H₁:

 con il test Z

 

 

 nel quale si è ottenuto Z = 1,71

-  non è stato possibile rifiutare l’ipotesi nulla, poiché corrisponde alla probabilità P = 0,087.

-  sempre in una distribuzione bilaterale e con la soglia di significatività minima a = 0.05.

 

Come già affermato, i due risultati non coincidono poiché l’errore standard è calcolato con due formule differenti. Con i dati dell’esempio

- per l’intervallo di confidenza

 

 

 si è ottenuto ES() = 0,1097

- per il test di significatività

 

 

si è ottenuto ES() = 0,1068

Ma è una differenza trascurabile, minore del 3% rispetto al valore inferiore.

 

FORMULA TEST BASED DI MIETTINEN

Un metodo rapido e approssimato per calcolare l’intervallo di confidenza di , cioè del valore vero del rapporto R tra due proporzioni, è stata proposta da Olli S. Miettinen nel 1976 (con l'articolo Estimability and estimation in case referent studies pubblicato su American Journal of Epidemiology Vol. 103, p.: 226-235). In letteratura è chiamato formula test-based di Miettinen, in quanto ricorre all’errore standard utilizzato nella formula per verificare la significatività della differenza tra due  proporzioni.

Tralasciando la lunga dimostrazione matematica e i passaggi logici che permettono di derivarla dalle formule precedenti, alla probabilità del 95% i limiti dell’intervallo di confidenza di r possono essere determinati

 con la formula

 dove

 e in parole

-   Z₁ è la Deviata Normale Standardizzata della differenza tra due proporzioni.

 

Questa riportata è la formula più semplice. Al posto della differenza, altre varianti sempre proposte da Miettinen utilizzano il rapporto R tra due proporzioni, tra due odds oppure tra due tassi. Ma appunto perché sono rapporti, hanno una distribuzione log-Normale, con forte asimmetria destra, che può essere ricondotta alla normale solamente con una trasformazione logaritmica. Il calcolo diventa più complesso e lungo, rispetto a questa formula. Per ulteriori informazioni sulla metodologia, si rimanda a testi specifici.

La corrispondenza con l’intervallo di confidenza calcolato in precedenza è dimostrata con l’esempio seguente.

 

 

ESEMPIO 3 (USO DELLLA FORMULA DI MIETTINEN, CON I DATI DELL’ESEMPIO 1). Dalle due proporzioni  e   ottenute con due campioni indipendenti, dove   = 108/180  e  = 60/120,

- ricavare il rapporto  e i suoi limiti di confidenza alla probabilità a = 0.05.

 

Risposta. Dopo aver calcolato  = 60/120 = 0,5   e    = 108/180 = 0,6

 si ottiene il rapporto .

Successivamente si deve stimare

 e il valore

 

 

Infine con

 si trovano

- il limite inferiore L₁ =  = 0,974

- il limite superiore L₂ =  = 1,479.

E’ semplice osservare che, con i dati dell’esempio 1, intorno al valore medio campionario  per il valore reale r, con la distribuzione normale applicata a , si erano stimati

-  il limite inferiore  =

-  il limite superiore =

E’ una dimostrazione empirica dell’equivalenza dei due metodi.

In questo caso, la formula di Miettinen determina un intervallo leggermente minore.