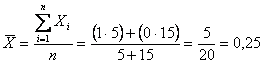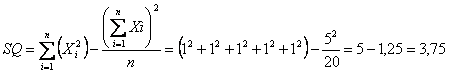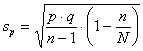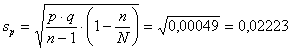PROPORZIONI E PERCENTUALI, RISCHI, ODDS E TASSI

5.3. PERCHE’ LA VARIANZA DI P E’ PQ E SUE CONSEGUENZE; VARIANZA E ERRORE STANDARD DI UNA FREQUENZA RELATIVA O ASSOLUTA, IN UNA POPOLAZIONE INFINITA E FINITA

Dopo la presentazione di alcuni termini del linguaggio tecnico, per l’analisi statistica di una proporzione è necessario riprendere i concetti presentati nella distribuzione binomiale.

Nei fenomeni binari, quindi con risposte Si-No, Vivo-Morto, che per l’analisi statistica sono tradotti in numeri con 1 – 0, in una popolazione di N individui nella quale X presentano la caratteristica A (indicata con 1), per essa

la proporzione p nella popolazione è

Quando da questa popolazione si estrae un campione di dimensione ,

la proporzione campionaria p è

e la proporzione q della caratteristica alternativa B (indicata con 0)

oppure

All’infuori dei due casi estremi, in cui = 0 oppure = 1

- se dalla popolazione si estraggono casualmente vari campioni di dimensione ,

- si hanno altrettante stime campionarie .

La proporzione , anche se può apparire una singola osservazione, in realtà è una media di un fenomeno binario, che come misure singole ha 0 oppure 1.

La sua varianza è la varianza di una media e può essere ricavata rapidamente con le due formule abbreviate seguenti:

- per la popolazione di individui, è

- per un campione di individui, è

Quando è grande, come quasi sempre richiesto per una stima sufficientemente accurata di una proporzione, le differenze tra le due formule sono minime. Per tale motivo, molti testi suggeriscono la prima anche per un campione.

Per comprendere in modo semplice che queste formule sono equivalenti a quelle classiche per il calcolo della varianza, è utile una dimostrazione elementare. Si supponga di avere somministrato un tossico ad un gruppo di 20 cavie e che tra esse 5 abbiano presentato sintomi di intossicazione.

La proporzione di individui intossicati

è = 0,25

e con la formula abbreviata

la sua varianza

è = 0,009868

(sono utilizzati più decimali, solo per dimostrare empiricamente l'uguaglianza dei due risultati).

Se a ognuno dei 5 soggetti intossicati si attribuisce convenzionalmente valore 1 e a ognuno degli altri 15 non intossicati valore 0,

- la media del fenomeno

è uguale a 0,25

- la sua devianza SQ

è uguale a 3,75

- e, da questa, la sua varianza

è uguale a 0,197368.

Ma questa è la varianza dei dati (0 e 1), mentre nel caso della proporzione p la varianza prima calcolata con la formula abbreviata è riferita alla media.

Poiché la deviazione standard della media (quindi l'errore standard),

e la varianza di una media è

con i dati del problema, si ottiene che

la varianza della proporzione media p

è = 0,009868.

Il risultato ( = 0,009868) è identico a quello ottenuto con il calcolo abbreviato.

Evidenziando nuovamente i concetti principali, questo risultato mostra che

- la varianza

è la varianza di una media p.

Nello stesso modo,

- la sua deviazione standard ()

in realtà è l'errore standard di p

e misura la dispersione delle medie di elementi, intorno al valore centrale.

Questi stessi concetti sono dimostrati in modo più scolastico, con una serie di passaggi logici e matematici da George W. Snedecor e William G. Cochran nel loro testo del 1974 Statistical Methods (6^th ed., The Iowa State University Press, Ames, Iowa, XIV + 593, vedi pag. 208).

(1)	(2)	(3)	(4)	(5)	(6)

La loro successione può essere schematizzata in 6 punti, riportati nelle colonne.

1) In una scala a intervalli o di rapporti la misura è continua e viene indicata con X; in una classificazione binaria in cui si misura la assenza - presenza del fattore, i valori possono essere tradotti in numeri con 0 e 1.

2) Raggruppando i dati per gli stessi valori, la frequenza relativa per la variabile continua è ; in una classificazione binaria, le frequenze relativa di è e la frequenza della relativa di è

3) La media , in una variabile continua è ; in una classificazione binaria è =

Quindi la prima conclusione è che

4) Per calcolare la varianza, si deve partire dagli scarti: per la variabile continua sono , mentre per la variabile discreta sono per i valori e per i valori .

5) Questi valori devono essere elevati al quadrato, ottenendo rispettivamente

- per la variabile continua ,

- per la variabile binaria per i valori e per i valori .

6) Considerato che , e sono frequenze relative, si ricava che la varianza =

E’ la seconda conclusione, che si voleva dimostrare.

La varianza della popolazione e quella campionaria della proporzione q (con )

sono identiche a quelle di p

Ne deriva che anche la deviazione standard di una proporzione p o q,

è totalmente determinata dal suo valore medio.

I calcoli sono semplici:

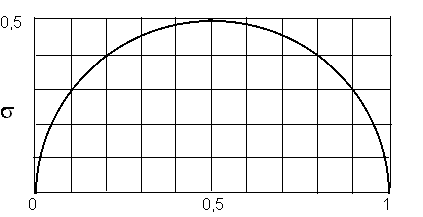
	0,5	0,4 o 0,6	0,3 o 0,7	0,2 o 0,8	0,1 o 0,9	0,05 o 0,95	0,01 o 0,99
	0,500	0,490	0,458	0,400	0,300	0,218	0,099

In una rappresentazione grafica, la corrispondenza risulta visivamente molto chiara.

Se in un diagramma cartesiano si riportano

- la media p sull’asse delle ascisse

- la sua deviazione standard s = sull’asse delle ordinate

è evidente il loro rapporto in campioni costanti di dimensioni .

Questa relazione pone problemi rilevanti, quando alle proporzioni o percentuali sono applicati test parametrici per il confronto tra le medie quali , quali il test t di Student e il test F di Fisher-Snedecor. Infatti non può essere rispettata una delle condizioni fondamentali di validità per confrontare due o più medie, rispetto alla quale questi test sono poco robusti:

- i vari gruppi a confronto devono avere la stessa varianza, anche quando le loro medie sono differenti.

Per confrontare la significatività della differenza tra medie diverse, si dovrà quindi

- nella statistica parametrica, ricorrere a trasformazioni dei dati, come quella in arcoseno;

- in altri casi, che saranno discussi in seguito, sarà più conveniente utilizzare test non parametrici;

Più recentemente, diffusi in particolare dai programmi informatici, ma spesso criticati nella letteratura statistica, sono proposti test t tra due medie e test ANOVA tra due o più medie, che possono essere utilizzati anche quando le varianze sono differenti, sulla base della proposta di Beherens-Fisher.

Un’altra conseguenza molto importante di questa relazione nelle proporzioni o frequenze relative

- tra la media

- e la sua varianza

che nel caso di conteggi o frequenze assolute diventa la relazione

- tra la media

- e la sua varianza

è che non è necessario avere misure ripetute per calcolare la varianza di un campione, ma è sufficiente conoscere la sua media.

CORREZIONE PER UNA POPOLAZIONE FINITA

Già diffusa da W. G. Cochran nel 1977 nel volume Sampling Techniques (3^rd ed., John Wiley, New York, p. 428) e, fra i testi internazionali di statistica applicata a maggior diffusione, riportata da Jerrold H. Zar nel volume del 1999 Biostatistical Analysis (4^th ed., Prentice Hall, Upper Saddle River, New Jersey, XII + 663 p. + App. 212 )

- quando la proporzione è stimata con un campione, che è una parte non trascurabile della popolazione intera, la varianza deve essere corretta utilizzando

1 - per la frequenza relativa p

- la varianza

- l’errore standard

2 – per la frequenza assoluta F con

- la varianza

- l’errore standard

dove

- = numero di unità che formano il campione raccolto,

- = numero di unità che formano la popolazione finita.

Il concetto è semplice:

- Se si calcola una proporzione ,

- utilizzando tutti gli elementi di una popolazione finita (quindi p),

- non esiste l’errore di campionamento.

Ad esempio, se una popolazione è composta solo di = 200 individui, come possono essere quelli sottoposti a una operazione all'anca presso la stessa clinica, e a un controllo successivo 120 pazienti si dimostrano totalmente riabilitati, dal conteggio su tutti gli individui della popolazione risulterà sempre che la proporzione di guariti della popolazione è anche se viene ripetuta da persone differenti.

La varianza della proporzione è uguale a 0.

Ma se, per stimare la proporzione vera o reale di guariti, si utilizza solamente un campione di pazienti (con ) e si ripete l'operazione ricampionando, tutte le volte le proporzioni rilevate saranno differenti tra loro e dalla proporzione vera .

Nella formule precedenti,

- è chiamata quota di campionamento (sampling fraction),

- può essere scritta anche come ed è chiamata correzione per la popolazione finita (finite population correction).

Dalle formule precedenti è ovvio dedurre che, quando ,

- la varianza e l’errore standard diventano uguali a 0,

- sia nella frequenza relativa che nella frequenza assoluta.

ESEMPIO 1. In una popolazione di 350 pazienti sottoposti a una operazione all'anca presso la stessa clinica, si vuole valutare dopo 6 mesi dall'operazione quale è la proporzione di individui che presentano ancora difficoltà di deambulazione. Dato il costo dell’indagine, è stato utilizzato un campione più ridotto. Dall’elenco completo, sono stati estratti casualmente 160 individui e sottoposti a controllo; tra essi 28 presentavano ancora difficoltà.

Calcolare la varianza e l’errore standard

- (a) della proporzione

- (b) della frequenza assoluta

Risposta. Prima di tutto, con = 350 e = 160 occorre calcolare la proporzione o frequenza relativa e la frequenza assoluta

ottenendo = 0,175 e = 61,25.

Con i dati dell’esperimento, si stima che nella popolazione di 350 pazienti

- la frequenza relativa di persone ancora non guarite è , anche se in realtà è stata calcolata solamente su 160 individui;

- la frequenza assoluta di persone ancora non guarite è , nell’ipotesi che la proporzione calcolata sul campione di 160 individui sia vera anche nella popolazione totale di 350.