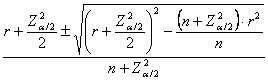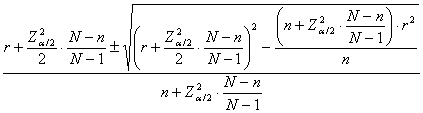PROPORZIONI E PERCENTUALI, RISCHI, ODDS E TASSI
5.4. INTERVALLO DI CONFIDENZA DI UNA FREQUENZA RELATIVA O ASSOLUTA CON LA NORMALE, IN UNA POPOLAZIONE INFINITA O FINITA; METODI GRAFICI PER L’INTERVALLO FIDUCIALE E LA STIMA DEL NUMERO DI DATI.
Per stimare i limiti
di confidenza di una proporzione o frequenza relativa
- l’errore
standard di
Nella ricerca
statistica, qualche volta è nota la proporzione vera o reale,
detta più tecnicamente anche proporzione della popolazione (p). Ad esempio, in
un processo industriale di selezione della frutta per scartare quella troppo
piccola o immatura, può essere nota quale sia la proporzione di scarti di
quella annata almeno a grandi linee. Ma con una macchina o un gruppo di
operai che selezionano
Conoscendo la
proporzione reale p di una popolazione, è possibile stimare la
distribuzione della proporzione campionaria
mediante la relazione
P
Essa significa che, - con una
probabilità di affermare il vero uguale a
- il valore
della proporzione campionaria
- si trova
tra la proporzione vera
Per la probabilità del 95% (a = 0.05) può essere scritta come
P
Gli stessi
concetti sull’intervallo di confidenza della proporzione
dove, in una distribuzione normale bilaterale (quindi a/2 in ogni coda), il valore di Z - per la probabilità del 95% è Z = 1,96 - per la probabilità del 99% è Z = 2,576 (spesso arrotondato nei testi in 2,58).
ESEMPIO 1 (DALLA POPOLAZIONE AL CAMPIONE). Con numerose ricerche è stato dimostrato che un tossico diluito in acqua alla concentrazione standard determina mediamente la morte del 30% degli individui della specie A. Alla probabilità del 95% entro quali limiti sarà compresa la frequenza relativa dei decessi in un esperimento con 80 individui?
Risposta. Con Z = 1,96 associata alla probabilità a = 0.05, con p = 0,3 e n = 80 come risulta dai dati dell’esempio
si ottiene - una
proporzione
- come limite inferiore ha L1 = 0,2 - come limite superiore ha L2 = 0,4.
ESEMPIO 2 (DALLA POPOLAZIONE AL CAMPIONE). Il tossico X determina la morte del 4% delle cavie utilizzate. Entro quali limiti alla probabilità del 99% sarà compresa la percentuale di decessi in un esperimento con 500 individui?
Risposta. Con Z = 2,58 associata alla probabilità bilaterale a = 0.01 e con p = 0,04 e n = 500
per il
valore campionario di frequenza relativa - si stima un intervallo che al 99% di probabilità è compreso tra - il limite inferiore L1 = 0,017 - il limite superiore L2 = 0,063.
Per un uso più immediato, sovente i testi di statistica applicata riportano, in forma grafica oppure in tabelle, il campo di variazione (alla probabilità 1-a prefissata) di una percentuale campionaria p, estratta da una popolazione con percentuale vera p. Un esempio dei valori, indicati come proporzioni, sono quelli della tabella successiva.
Intervallo di variazione di
della popolazione e alla dimensione
alla probabilità del 95 % .
La sua lettura è semplice. Per esempio, estraendo da una popolazione che ha una proporzione p = 0.30 un campione di 20 individui, la percentuale campionaria p con probabilità del 95% è compresa nell’intervallo tra .099 e .501. E’ un intervallo obiettivamente molto grande. Ma deriva dal fatto che una classificazione qualitativa fa perdere molta informazione, rispetto a una misura quantitativa, come utilizzata nel capitolo precedente. Mantenendo costante la probabilità a di un errore di I Tipo, all’aumentare del numero di osservazioni (n) il campo di variazione della stessa percentuale campionaria p si riduce. Continuando l’esempio sempre per p = 0.30 e a = 0.05, - con 50 osservazioni p è compresa tra 0,173 e 0,427; - con 100 osservazioni tra 0,210 e 0,390; - con 200 osservazioni tra 0,236 e 0,364; - con 500 osservazioni tra 0,260 e 340; - con 1000 osservazioni tra 0,272 e 0,328.
La tabella mostra anche che, alla stessa probabilità di affermare il vero del 95% e con lo stesso numero (n) di osservazioni, - il campo di variazione di p è massimo quando p= 0,50 - e minimo verso gli estremi 0 e 1, in modo simmetrico.
Nella tabella, è utile osservare che non sono stati riportati i valori dell’intervallo fiduciale o di confidenza per le proporzioni p vicine a 0 né per quelle vicine a 1, con dimensioni campionarie (n) ridotte. Il motivo è che - quando i campioni sono piccoli e p è vicino agli estremi, - la distribuzione non può essere approssimata alla normale standardizzata. Nella stima
dell’intervallo di confidenza, essa potrebbe fornire estremi L1
e L2 negativi oppure superiori a 1, che sono valori
privi di significato per una proporzione. Questa anomalia deriva dal
fatto che con valori vicino agli estremi, la distribuzione delle probabilità
Molto spesso, negli esperimenti in laboratorio e nella raccolta dei dati in natura, la situazione è opposta a quella appena illustrata: con un esperimento, - è frequente ottenere la stima di una proporzione campionaria p (r/n), - dalla quale si vuole ricavare la stima della frequenza relativa p, chiamata proporzione vera oppure proporzione della popolazione.
Come suggerito da vari autori di testi di statistica, tra i quali W. G. Cochran (vedi del 1977 il testo Sampling Techniques, 3rd ed. John Wiley, New York, 428 pp.), il modo più semplice - per stimare l’intervallo di confidenza di una proporzione campionaria p, - che sia stata calcolata su n dati, - estratti casualmente da una popolazione teoricamente infinita e con proporzione reale p, utilizza la distribuzione normale e la sua deviazione standard:
dove - per la probabilità del 95% (a = 0.95) il valore di Z è 1,96 - per una probabilità del 99% (a = 0.99) il valore di Z è 2,58.
Scritto in modo più formale, P
ESEMPIO 3 (DAL CAMPIONE ALLA POPOLAZIONE). In un campione di 80 fumatori, il 35% ha presentato sintomi di polmonite. Quali sono i limiti entro i quali alla probabilità del 95% e del 99% si troverà la media reale (p) di individui con sintomi di polmonite, nella popolazione dei fumatori?
Risposta. Dopo aver individuato i termini della domanda
si calcola
entro quale intervallo si troverà la proporzione vera
1 – Con probabilità di affermare il vero
del 95% ( la proporzione vera p si troverà tra
- il limite inferiore L1 = 0,2448 - il limite superiore L2 = 0,4552.
2 - Con probabilità di affermare il vero
del 99% ( la proporzione vera p si troverà tra
- il limite inferiore L1 = 0,2115 - il limite superiore L2 = 0,4885.
La probabilità di errore a o di I Tipo che è associata all’intervallo fiduciale di p ha un significato identico a quello della probabilità a per l’intervallo di confidenza della media vera m: - se dalla popolazione si estraessero tutti i possibili campioni e si costruissero tutti i possibili intervalli di confidenza, - una frazione uguale a 1-a comprenderebbe il valore reale di p, - mentre la rimanente frazione a non lo comprenderebbe.
ESEMPIO 4 (DAL CAMPIONE ALLA POPOLAZIONE). Su un campione di 148 individui che vivono in un’area ad alto inquinamento atmosferico, 31 hanno presentato sintomi di malattie dell’apparato respiratorio. Stimare l’intervallo di confidenza della proporzione p, detta proporzione vera o della popolazione, al 95% di probabilità.
Risposta. Per utilizzare la formula appena presentata, il calcolo dell’intervallo, entro il quale si troverà la proporzione reale p con una probabilità del 5% di errare, richiede di conoscere - p = proporzione del campione, che è 31/148 = 0,209 - n = numero di dati del campione, che è 148 - Z per la probabilità a = 0.05 bilaterale, che è 1,96
Da essi, si stima l’intervallo
fiduciale o intervallo di confidenza (confidence
interval) di
- per limite inferiore
è L1 = 0,142 - per limite superiore
è L2 = 0,276.
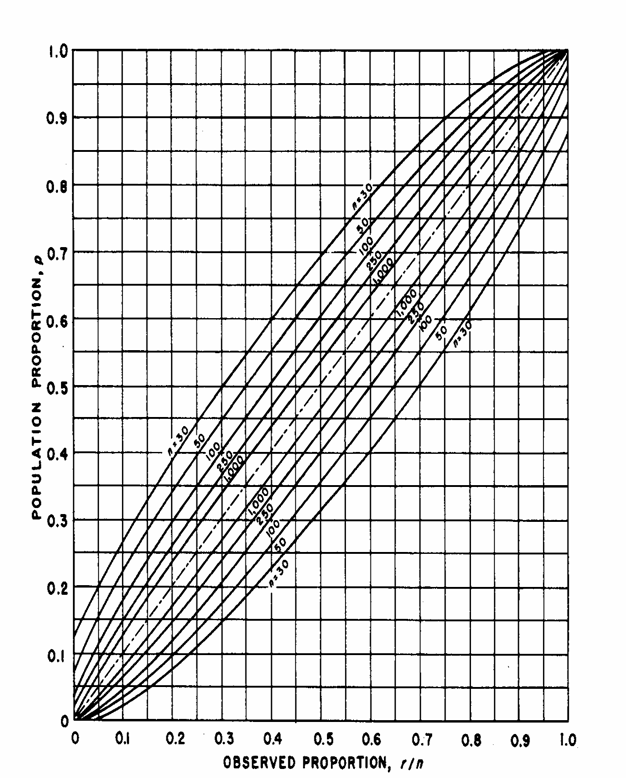
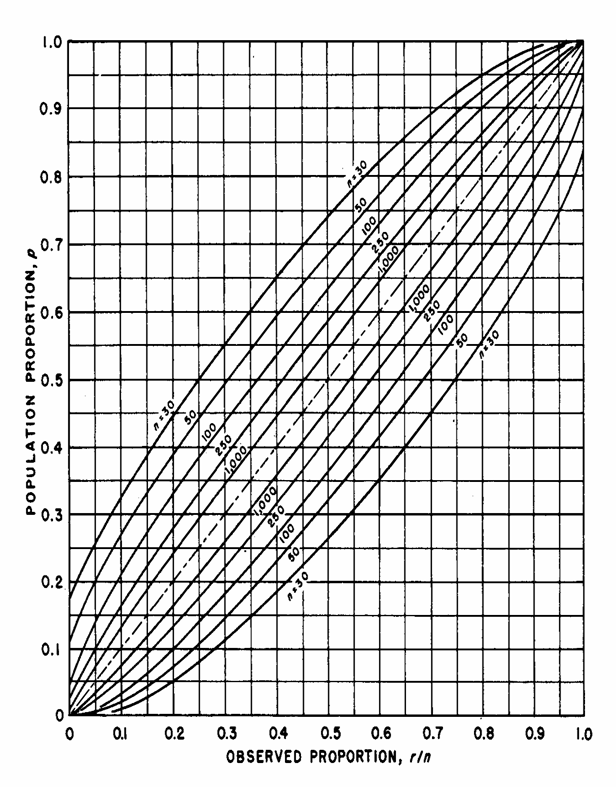
UN METODO GRAFICO In modo molto più rapido, seppure più approssimato, è possibile ottenere gli stessi risultati sull’intervallo confidenza di p ricorrendo a tabelle, come quella illustrata in precedenza. In altro metodo simile alle tabelle, operativamente più lungo ma concettualmente altrettanto semplice, è l’uso di grafici, come i due riportati nelle pagine seguenti. Tratti dall’articolo di C. J. Clopper e E. S. Pearson del 1934 The Use of Confidence or Fiducial Limits Illustrated in the Case of the Binomial (pubblicate su Biometrika Vol. 26, pp.: 404-413) sono riportati anche nel manuale del Dipartimento di ricerca della Marina militare Americana, pubblicato nel 1960, dal titolo Statistical Manual (by Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, Research Department U. S: Naval Ordnance Test Station, Dover Pubblications, Inc., New York, XVII + 288 p.).
E’ un metodo che ora è superato dall’uso dei computer, con i quali è possibile una stima sia rapida, sia precisa. Ma è sempre utile una conoscenza dei vari metodi storici, seppure a volte obsoleti, per giustificare in modo più completo la scelta del test. Queste curve
di confidenza delle proporzioni (confidence belts for proportions),
delle quali sono state riportate solamente i grafici di uso più frequente (a = 0.05 e a = 0.01), sono valide
per campioni abbastanza grandi. In questo caso, gli autori del testo
definiscono tale limite quando
L’uso delle curve di confidenza è semplice.
a = 0.05 Strisce di
confidenza per le proporzioni campionarie
a = 0.01 Strisce di
confidenza per le proporzioni campionarie
Calcolata la proporzione
campionaria
e dopo aver scelto il grafico per la probabilità a desiderata, esse servono: 1 - per trovare i limiti
l’intervallo di confidenza di
2 – per valutare
quale sia la dimensione campionaria
Ovviamente si ottengono misure approssimate, - sia per la natura stessa del metodo grafico, - sia per
la natura discreta dei dati originali, i conteggi
L’uso del grafico è illustrato nei due esempi successivi, con la presentazione di due situazioni classiche della ricerca applicata: 1 – (esempio 5)
dopo aver trovato una proporzione
2 –
(esempio 6) stimare quale deve essere la dimensione
ESEMPIO 5 (DAL CAMPIONE ALLA POPOLAZIONE) L’analisi di un campione di 250 sacche di plastica per la conservazione del sangue ha rilevato che, dopo un mese di custodia in frigo, quelle degradate erano esattamente 30, corrispondenti al 12% del campione analizzato. Con una probabilità del 95% di affermare il vero, indicare quale è la proporzione vera di scarti con quel metodo di conservazione.
Risposta. Dopo aver scelto la figura per a = 0,05 - sull’asse
delle ascisse si individua il punto che identifica
- salendo
verticalmente, si incontra la curva per
- la prima in un punto che sull’asse delle ordinate corrisponde alla proporzione p = 0.08, - la seconda in un punto che sull’asse delle ordinate corrisponde alla proporzione p = 0.17. In conclusione, nella popolazione la percentuale di sacche degradate è compreso tra l’8% e il 17%. Questa affermazione ha una probabilità a = 0,05 di essere errata (o del 95% di essere vera). E’ importante
osservare che, a differenza di quanto succede con la distribuzione normale, i
due limiti dell’intervallo di confidenza non sono simmetrici rispetto alla
proporzione
ESEMPIO 6
(STIMARE
Risposta.
Non avendo alcuna idea sul valore che è possibile trovare, per il
principio di cautela occorre mettersi nella condizione meno favorevole.
Con le proporzioni, è quando il campione è
Scelto il grafico
per a = 0.05 e salendo
verticalmente da
- per le
due curve
- per le
due curve
Il primo
intervallo (0,14) è troppo grande, rispetto al valore massimo desiderato di
0,10; quindi un campione di dimensioni
Il secondo
intervallo (0,06) è piccolo, rispetto al valore massimo desiderato di 0,10;
quindi un campione di dimensioni
Si deve ricavare una stima, utilizzando l’interpolazione lineare.
Poiché la dimensione massima individuata
mediante le curve è
Dopo aver valutato che le dimensioni del campione variano tra 250 e 1000, - si calcola che, nell’unità di
misura
- la quantità minore
- per cui la distanza tra i due rapporti è: 3 = 4-1.
Successivamente, per la lunghezza degli intervalli, si stima la distanza: 0,14 - 0,10 = 0,04 - e la distanza 0,14 – 0,06 = 0,08
Dalla relazione lineare
si ricava che il valore
Da questo rapporto si perviene alla stima conclusiva:
Il campione deve avere
In un paragrafo successivo, questa stima è effettuata con l’uso della distribuzione normale. Per una sua presentazione dettagliata si rimanda ad esso. Tuttavia per un confronto dei risultati, con essa
si ottiene una
stima abbastanza simile sulla dimensione del campione richiesto con l’uso
del grafico e l’interpolazione lineare:
Nell’ultima formula, -
Quando a
priori, almeno in modo approssimato, la proporzione
Ad esempio (usando la distribuzione normale), se il tecnico avesse avuto una indicazione esterna, come aver letto su un rapporto oppure aver ricavato da un esperimento preliminare che la quantità di sacche degradate approssimativamente era del 12%, mantenendo costanti Z = 1,96 e d = 0.05 avrebbe ricavato
una stima
FORMULE PER UNA FREQUENZA ASSOLUTA O CONTEGGIO L’intervallo di confidenza può essere calcolato anche per la frequenza assoluta o conteggio, con una formula più complessa di quella utilizzata per la frequenza relativa, ma sulla base di concetti del tutto uguali. E’ sufficiente illustrare la metodologia con un esempio. Riprendendo i dati dell’esempio 5, nell’analisi di un lotto di 250 sacche di plastica per la conservazione del sangue si ipotizzi di voler stimare il numero o frequenza assoluta di quelle che saranno quelle da scartare, in lotti di 250 sacche, sempre alla probabilità a = 0.05 che tale affermazione sia errata. Nel Manuale della Marina Americana, già citato, è proposta la formula
dove -
-
Nel caso di una popolazione finita, come può essere un
lotto di
tale formula diventa
dove, - rispetto al prima formula, la quantità
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
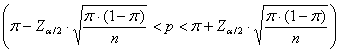 = 1-
= 1-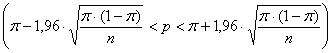 = 0,95
= 0,95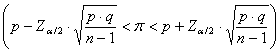 = 1-
= 1-