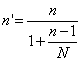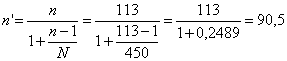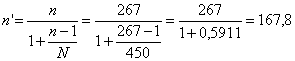PROPORZIONI E PERCENTUALI, RISCHI, ODDS E TASSI
5.6. CALCOLO DEL CAMPIONE MINIMO NECESSARIO, PER LA STIMA DI UNA PROPORZIONE CAMPIONARIA CON UN ERRORE MASSIMO PREFISSATO
Quando p e q sono non troppo vicini a 0 oppure a 1, è possibile utilizzare la distribuzione normale anche per calcolare il numero n di osservazioni, che è necessario per ottenere una stima p (quindi anche q) con un errore inferiore alla quantità d prefissata. A tale scopo, W. G. Cochran (nel testo già citato del 1977 Sampling Techniques, 3rd ed. John Wiley, New York, 428 pp.) propone
dove -
Quando, ovviamente in una popolazione finita di dimensione N, il numero n del campione ne rappresenta una frazione non trascurabile, si può pervenire ad una stima corretta n’, con
ESEMPIO 1. Nella popolazione, la proporzione di individui affetti da allergie è p = 0,12. La presenza di sostanze inquinanti aumenta tale proporzione. Quanti individui occorre analizzare, per ottenere una stima di p che abbia un errore massimo di 0,06 con un rischio di sbagliare a = 0.05?
Risposta. Con p = 0,12 (quindi q = 0,88) d = 0,06 Z = 1,96 per a = 0.05 bilaterale è richiesto
un campione di almeno
Nell’utilizzo di queste formule per il
calcolo di
1 - Il
valore d, cioè l’errore
massimo accettabile, deve essere espresso in proporzione come il
valore della media
- se
si indica che il valore reale
- il limite inferiore L1= 0,19 (0,25 - 0,006) - il limite superiore L2 = 0,31 (0,25 + 0,06).
2 - Un altro
aspetto importante del valore d da tenere in considerazione è il suo effetto sulla
dimensione
- un dimezzamento dell’errore d massimo accettato - comporta
che le dimensioni
Ad esempio con d = 0,03 al posto di d = 0,06 precedente
si ricava
Quindi attenzione
a non diminuire eccessivamente il valore d, poiché la
quantità
3 - Il
valore d tuttavia è legata al valore
Diminuire d quando
Ad esempio con d = 0,02 e p = 0,04
si ricava
Gli effetti sono simmetrici, per cui il discorso è ugualmente valido per la proporzione p = 0,96.
4 – Ha un peso non trascurabile, seppure inferiore, anche
la scelta dell’errore
con Z = 2,576
si ricava
ESEMPIO 2. In piccolo centro abitato nel quale vivono 450 persone adulte, è presente un’azienda che scarica fumi ritenuti tossici. Nella popolazione, la proporzione di individui affetti da allergie è p = 0,12. La presenza di sostanze inquinanti aumenta tale proporzione. Quanti individui occorre analizzare, per ottenere una stima di p che abbia un errore massimo di 0,06 con un rischio di sbagliare a = 0.05? Nel caso di una popolazione infinita, si era stimato n = 113. Nel caso di una popolazione con N = 450, quanti individui occorrerà sottoporre a visita di controllo?
Risposta. Con n = 113 e N = 450, il numero minimo di individui da sottoporre a visita per mantenere gli stessi parametri dell’esempio precedente è
n’ = 91. Il numero di individui da controllare è minore: scende da 113 a 91.
Nella prassi della ricerca, è frequente il caso in cui a priori non è possibile indicare il valore di p, neppure in modo approssimato. Quando si analizzano gli effetti di una nuova sostanza tossica, somministrata in dose elevata a cavie, non sempre è possibile stimare quale sarà la proporzione p di individui che risulteranno positivi, neppure in modo largamente approssimato: potrebbe essere solamente p = 0,03 ma anche p = 0,41.
Anche in questa condizione, è possibile stimare il numero n di dati minimo per misurare p con un errore che non superi la quantità d prefissata alla probabilità a. Ma occorre porsi nella situazione sperimentale peggiore, cioè quella con la varianza massima. Poiché la varianza è massima quando p = 0,5 la formula precedente
diventa
Essa può essere semplificata in
Anche in questo caso, se la popolazione è finita e n è una quota non trascurabile di N, si può pervenire ad una stima corretta n’, utilizzando la formula già presentata:
ESEMPIO 3. Riprendendo i dati dell’esempio 1, quanti individui occorre analizzare per ottenere con un rischio di sbagliare a = 0.05 una stima campionaria della proporzione p di individui affetti da allergie, che abbia una differenza massima d = 0,06 rispetto al valore ignoto della popolazione?
Risposta. Nell’ipotesi peggiore per le dimensioni del campione e quindi - con p = 0,5 - per una differenza massima d = 0,06 - e alla probabilità a = 0.05 bilaterale quindi con Z = 1,96 è richiesto
un campione di almeno 267 persone. Nell’esempio 1 (con p = 0,12), si
era stimato
ESEMPIO 4. Se la popolazione complessiva N è di 450 individui e il campione stimato n = 267, quante persone occorrerà sottoporre a visita di controllo?
Risposta. Con n = 267 e N = 450, il numero minimo di individui da sottoporre a visita è
n’ = 168. Nell’esempio 2
(con p = 0,12), si era ottenuto
Le due ultime
conclusioni sono due dimostrazioni empiriche dell’importanza e della
convenienza di analizzare seriamente il problema, prima di effettuare un
campionamento. Avere un’idea su quale sarà la proporzione
Nella ricerca applicata, è quanto si richiede quasi sempre a uno statistico professionale. Da alcuni anni, con una sempre maggiore richiesta di cultura statistica, per ogni progetto serio di ricerca si richiede sempre che venga espressa la dimensione del campione da raccogliere, per rispettare i parametri fissati. Un errore in queste ipotesi può determinare conseguenze gravi, tali da annullare buona parte della validità della ricerca. E’ semplice dedurre che, per esempio, se si ipotizza una proporzione p = 0,12 e poi nell’esperimento a posteriori si trova p = 0,47 la stima della proporzione reale p avrà un errore a o un intervallo d maggiori di quanto richiesto nella ricerca. L’impostazione di una ricerca richiede anche una competenza elevata nel settore, non solamente buone conoscenze statistiche.
|
|
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |