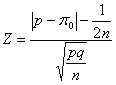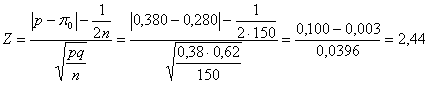PROPORZIONI  E  PERCENTUALI,  RISCHI,  ODDS  E  TASSI

 

 

5.7. IL CONFRONTO TRA UNA PROPORZIONE CAMPIONARIA E UNA PROPORZIONE ATTESA CON IL TEST Z; DIMENSIONE MINIMA DEL CAMPIONE, PER L’USO DELLA DISTRIBUZIONE NORMALE.

 

 

Nel capitolo 3 sul chi quadrato, è stato presentato l’uso della distribuzione normale Z

-  sia per il confronto di una proporzione osservata con una proporzione attesa,

-  sia per il confronto tra due proporzioni osservate,

 quando i campioni sono di grandi dimensioni.

Infatti, in tali condizioni, esiste corrispondenza (già illustrata) tra distribuzione  con un gdl e la distribuzione Z:

Per una verifica empirica, è sufficiente controllare sulle tabelle dei valori critici che per a = 0.05

- nella distribuzione normale bilaterale si ha Z = 1,96

- nella distribuzione chi-quadrato con un gdl si ha c² = 3,84

 

Nell’analisi statistica dei dati, è quindi possibile utilizzare indifferentemente metodi che si rifanno alle due distribuzioni.

Ad esempio, nello studio dell’effetto di 4 farmaci con i dati seguenti

 

 

 

 

 mediante  la distribuzione normale o test Z è possibile verificare

1 - se la proporzione  di guariti con il farmaco A (dove  = 0,339 o 33,9%) è statisticamente  differente da una proporzione  prefissata;

 

2 – se la proporzione di guariti del farmaco C (con  = 0,314) è statisticamente differente  da quella del farmaco D (con  = 0,205).

 

Per confrontare tra loro l’effetto di tre o più farmaci sulle frequenze di guarigione, è opportuno ricorrere al test  o al test G, già presentati. Quindi si utilizzano i dati della tabella 2 x k seguente:

 

 

 

Ma, come illustrato nel capitolo 3, è possibile servirsi di queste due distribuzioni  ( o G ) anche per risolvere i primi due problemi.

 

Con  i test sono sempre bilaterali, poiché le ipotesi alternative all’ipotesi nulla

H₀: p_A = p_B = p_C = p_D

 sono sempre multiple, esprimibili con la frase

H₁: almeno una p è diversa dalle altre

oppure

H₁: almeno due p sono differenti tra loro  o il test G

 

Rifiutata l’ipotesi nulla, con metodi più sofisticati è possibile poi verificare tra quali proporzioni  campionarie esiste una differenza significativa. La prassi di applicare il test generale prima di passare a confronti a coppie, è un principio di cautela illustrato nei paragrafi dedicati ai confronti multipli. Non tutti gli autori concordano su questa cautela, ritenendo che i test siano equivalenti. In realtà la prassi di applicare un test generale, prima di utilizzare i confronti singoli, dipende dalla probabilità a complessiva, che deve essere calcolata tenendo presenti le singole probabilità a di tutti i confronti effettuati. Con il metodo generale, la stima è data molto semplicemente dal valore di a prescelto.

 

Se in un esperimento con  casi, un numero  di essi è risultato positivo,

- per confrontare se è statisticamente significativa

- la differenza tra la proporzione (con ) e una proporzione  di una popolazione,

- è possibile utilizzare sia  (1) la frequenza assoluta, sia  (2)  la frequenza relativa:

 

1 – con la frequenza assoluta  

2 – con la frequenza relativa  

 

La parte – 0,5 (spesso scritta – )

-  riportata al numeratore nella formula con la frequenza assoluta,

-  è chiamata correzione per la continuità o correzione di Yates

(Frank Yates, inglese 1902–1994. Laureato in matematica, assistente di Ronald Fisher nel 1931 quando lavora nell’istituto di ricerche agrarie Rothamsted Agricultural Research Institute. Diventatone direttore, nel 1954 dirige l’installazione del primo computer inglese, l’Elliot 401, scrivendo programmi per l’analisi della varianza).

 

La correzione di Yates è motivata dal fatto che  è un conteggio, quindi un numero intero che viene collocato su una scala continua, come è il valore .

Ad esempio, se nella tabella precedente prendiamo

-  che i guariti con il farmaco A sono  = 37 e il valore atteso era  = 40,3

-  occorre considerare che il valore 37 non è da intendere come un valore continuo (37,00) ma un valore di una unità, collocato sul 37;

-  quindi l’unità 37 su una scala continua occupa lo spazio unitario da 36,5 a 37,5.

Ne deriva che la distanza  

 in realtà è

 = 2,8

I suoi effetti sono ovvii: il valore di Z risulta minore.

Con l’uso di una frequenza relativa, la correzione di Yates diventa 

 

Per utilizzare la distribuzione Z in test sulle proporzioni, si richiede che le dimensioni  del campione siano abbastanza grandi. Questo valore  non è costante, ma dipende da quello della proporzione .

Quando  è compreso tra 0,3 e 0,7 è ritenuto adeguato un campione di dimensioni .

Negli altri casi, è ritenuto adeguato solamente

 un campione di dimensioni

 dove al denominatore

-  è da intendere il valore minore tra  e .

Devono essere esclusi i valori estremi, minori di 0,02  oppure maggiori di 0,98.

Ovviamente, come è possibile vedere in altre parti del testo, non esiste uniformità tra le diverse scuole di statistica anche su questo piccolo problema su quando un campione può essere definito abbastanza grande: alcune richiedono un campione  ancore maggiore, altre si accontentano di un valore minore.

 

ESEMPIO 1. Calcolare le dimensioni minime  del campione per poter utilizzare la distribuzione normale Z, quando (a)  = 0,5 e  (b)  = 0,92.

Risposte.

A) Quando  = 0,5 si ha che anche  = 0,5;

Con il calcolo

 si stima che il campione minimo sarebbe .

 

B) Quando  = 0,92 si ha che anche  = 0,08;

Ne deriva

 che il campione minimo sarebbe .

 

Quando ci confronta il valore sperimentale  con un valore atteso o teorico , questo test per un campione può essere sia bilaterale o a due code, sia unilaterale o a una coda.

Nel caso di un test bilaterale, le ipotesi sono formalmente scritte come

H₀:         contro        H₁:

 dove l’ipotesi nulla significa che

- la proporzione  della popolazione, dalla quale è stato estratto il campione di proporzione , è uguale a quella  della popolazione di confronto;

- oppure, espressa con altre parole, il campione con proporzione  è stato estratto dalla popolazione con proporzione .

 

Nel caso di un test unilaterale, l’ipotesi alternativa è scritta come

H₁:         oppure         H₁:

La loro ipotesi nulla,

-  in alcuni testi, è scritta come nel caso bilaterale H₀:

- in altri e formalmente più corretta, considera anche il segno opposto.

Pertanto le ipotesi unilaterali possono essere scritte come

H₀:         contro        H₁:

oppure

H₀:         contro        H₁:

 

ESEMPIO 2.  Un farmaco contro l’asma determina una netta riduzione dei sintomi nel 28% dei pazienti, già dopo una settimana di somministrazione. Per valutare gli effetti di un nuovo principio attivo, su 150 pazienti ai quali è stato somministrato nelle stesse condizioni, il numero di individui con la stessa riduzione dei sintomi è stato 57. Il nuovo principio attivo è statisticamente migliore?

 

Risposta. La proporzione di individui che hanno risposto positivamente alla somministrazione del farmaco nel campione con  = 150 è stato

.

 

Il test è unilaterale, poiché si tratta di decidere se la proporzione reale  del nuovo farmaco, della quale p = 0,38 è solamente la risposta di un campione, è statisticamente maggiore di  = 0,280.

In termini più formali si scrive

H₀:         contro        H₁:

 Usando la formula con

-  la frequenza relativa

 

 

 si stima Z = 2,44.

 Usando la formula con

- la frequenza assoluta

 

 

 si stima lo stesso valore Z = 2,44 (a meno delle approssimazioni nei calcoli)

In una distribuzione normale unilaterale, a Z = 2,44 corrisponde una probabilità P = 0,007.

Questo risultato significa che,

-  se H₀ fosse vera, cioè se la proporzione vera p di guarigione del farmaco nuovo fosse 0,28 come per il farmaco vecchio,

-  esiste una probabilità P = 0,007 che il farmaco nuovo dia in risultato come quello ottenuto o ancora migliore.

Una probabilità P = 0,007 ( o del 7 per mille) è oggettivamente bassa. Di conseguenza, si decide di rifiutare l’ipotesi nulla e quindi implicitamente di accettare l’ipotesi alternativa.

La dizione estesa di tale conclusione è: con probabilità P = 0,007 di errare (perché può essere che H₀ sia vera e che il risultato sia stato ottenuto effettivamente solo per caso) rifiuto l’ipotesi nulla e accetto l’ipotesi alternativa.

Oppure, più sinteticamente: con probabilità P = 0,007 il farmaco nuovo è statisticamente migliore.