|
INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT
6.17. LIMITI DI TOLLERANZA E POPULATION COVERAGE, CON METODI PARAMETRICI
Nella gestione dell’ambiente e in un processo industriale, il termine limiti di tolleranza ha varie accezioni. Quella più nota, diffusa quotidianamente dai media e che nei non esperti genera fraintendimenti con l’analisi statistica, fa riferimento ai valori di legge per situazioni ambientali, come la qualità dell’acqua e dell’aria, non diversamente da qualsiasi altro prodotto alimentare che può danneggiare la salute. Ad esempio, per la qualità dell’aria, vengono rilevati il biossido di zolfo (SO2), il biossido di azoto (NO2), il monossido di carbonio (CO), l’ozono (O3), la frazione delle polveri inalabili caratterizzate da un diametro aerodinamico medio che è inferiore a 10 mm (PM10). Norme, leggi o decreti individuano il Valore Limite e il Margine di Tolleranza di questi inquinanti. A concentrazioni ancora superiori, si parla di Livello di Attenzione e di Livello di Allarme. Sempre per chiarire i concetti e non generare equivoci con l’analisi statistica, è utile rivedere la definizione di questi limiti, individuati a partire da effetti medici, biologici o ambientali. Il Valore Limite è il livello fissato al fine di evitare, prevenire o ridurre gli effetti dannosi sulla salute umana o per l'ambiente nel suo complesso. Il Margine di Tolleranza è la percentuale tollerata di superamento del valore limite. Lo Stato di Attenzione è la situazione che, se persistente, attiva lo stato di allarme. Lo Stato di Allarme è la situazione che può determinare una condizione di rischio ambientale e sanitario. Per migliorare costantemente la situazione, si fissa l’Obiettivo di Qualità, definito come il valore medio annuale di riferimento, da raggiungere e rispettare a partire da una determinata data. In molti settori industriali, dalla meccanica alla farmaceutica, sono utilizzati principi analoghi, per i parametri attinenti la funzione del prodotto. I limiti sono espressamente dichiarati e ogni singolo prodotto deve rispettare le caratteristiche fissate, per non essere scartato.
L’intervallo di tolleranza statistico o i limiti di tolleranza naturale (tolerance interval, natural tolerance limits, ) è un concetto analogo all’intervallo di confidenza o intervallo di fiducia. Ma mentre questo ultimo è riferito a una media o a una varianza, cioè alla distribuzione di un parametro, l’intervallo di tolleranza fa riferimento alla distribuzione dei dati e indica i limiti entro i quali è atteso che si trovi una proporzione specifica della popolazione di dati. L’intervallo di tolleranza può essere stimato sia con metodi parametrici, sia con metodi non parametrici. In questo paragrafo sono presentati i metodi parametrici.
Quando - la distribuzione dei dati è normale e - sono note nota sia la deviazione standard della popolazione s, sia la media reale m,
per individuare i
limiti della distribuzione delle medie campionarie
mentre per i singoli valori, quindi per individuare i limiti di tolleranza, si usa
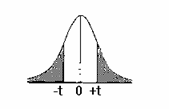
I limiti di tolleranza bilaterale stabiliscono un intervallo che comprende almeno la proporzione P (in %) dei dati della popolazione, considerando contemporaneamente le due code. Ad esempio, il 95% dei dati in una distribuzione bilaterale è compreso tra
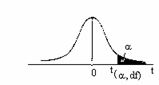
Ma spesso il limite, come negli inquinanti e in vari prodotti industriali, è collocato solo in una coda. In tal caso, si usa
Ad esempio,
individua - il limite di tolleranza unilaterale superiore (ls) - e esclude il 5% dei valori maggiori.
Ma quasi sempre la richiesta di conoscenza è nell’altra direzione: come, dai dati di un campione, pervenire alla conoscenza delle caratteristiche della popolazione. In tal caso, se - la distribuzione dei dati è normale e
- è ignota la
deviazione standard
s della popolazione, per cui si utilizza la deviazione
standard campionaria
-
contemporaneamente è ignota anche la media
m reale o della popolazione, per cui si
utilizza la media campionaria
l’intervallo di
confidenza o di fiducia della media
m della popolazione è stimato a partire
dalla media campionaria
dove - il valore di t è individuato nella tabella dei valori critici, da a e dal numero di gradi di libertà. A differenza della distribuzione Z, che può servire per definire i limiti sia di una media sia di una proporzione prestabilita di dati, la distribuzione t di Student è specifica per le medie campionarie.
Per una proporzione di popolazione a partire da dati campionari, si utilizza l’intervallo di tolleranza delimitato da
dove
-
- la probabilità
- la proporzione P minima di dati, che è compresa nell’intervallo di tolleranza (le tabelle allegate riportano solamente tre proporzioni di dati P = 0,90 P = 0,95 P = 0,99); in termine tecnico, la percentuale P è chiamata population coverage;
- il numero
Per gli intervalli di tolleranza, la tabella dei valori critici della distribuzione bilaterale è stata divulgata da A. H. Bowker nel 1947 con l’articolo Tolerance limits for normal distribution, (pubblicato nel volume Selected Techniques of Statistical Analysis, p: 97-110, ed. by Eisenhart, Hastay and Wallis, McGraw-Hill, New York). A differenza di quella riportata nella pagina successiva, la tabella originale di Bowker contiene - cinque valori della proporzione P (population coverage), - per quattro valori della probabilità a,
- e include un
numero maggiore di dimensioni
Ad essa si rimanda per una maggiore ampiezza di stime degli intervalli di tolleranza. I valori possono comunque essere stimati a partire da una distribuzione normale, con il metodo descritto nel prosieguo del paragrafo. Per meglio comprendere la corrispondenza tra i valori k, la distribuzione normale e la distribuzione t di Student, si osservi che con un numero infinito di osservazioni (ultima riga della prima tabella) il valore di k per la proporzione P = (1 - a) x 100coincide - sia con i valori Z alla stessa probabilità a, - sia quelli del t di Student per la stessa probabilità e gdl infiniti.
Infatti nella tabella è semplice osservare che - k = 2,576 per P = 99% e a = 0.01
FATTORI K PER LIMITI DI TOLLERANZA A DUE CODEDELLA PROPORZIONE P ALLA PROBABILITA’ a
CON
ESTRATTO DA UNA POPOLAZIONE CON DISTRIBUZIONE NORMALE
FATTORI K PER LIMITI DI TOLLERANZA A UNA CODADELLA PROPORZIONE P ALLA PROBABILITA’ a
CON
ESTRATTO DA UNA POPOLAZIONE CON DISTRIBUZIONE NORMALE
ESEMPIO 1. (STIMA
DI UN INTERVALLO DI TOLLERANZA BILATERALE). Un campione di 20 misure della
quantità di principio attivo presente in un farmaco ha permesso di calcolare
la media Stimare i limiti di tolleranza statistica per una proporzione uguale o superiore al 95% di tutta la produzione, alla probabilità di 1% di commettere un errore di I tipo.
Risposta. Dalla tabella dei valori k dei limiti di tolleranza a due code, per
si ricava
Di conseguenza, con
- il limite inferiore li = 9,72 - il limite superiore ls = 10,74. Con probabilità di errare non superiore all’1%, si può affermare che almeno il 95% di tutta la produzione ha un valore che è compreso tra 9,72 e 10,74.
Successivamente all’analisi statistica, l’accettabilità di tale intervallo di tolleranza deve essere valutata entro la disciplina scientifica. Ad esempio, se l’intervallo appena calcolato, come ipotizzato, fosse la differenza tra i mg. di principio attivo in singole fiale di un farmaco, facilmente tale variazione è largamente ammissibile, in quanto biologicamente trascurabile. Fosse invece quella in cm. del diametro di un pezzo meccanico da inserire in un altro, presumibilmente il campo di variazione sarebbe totalmente inaccettabile, in quanto impedirebbe il corretto funzionamento dello strumento.
La tabella dei valori k può essere ricavata da una distribuzione normale. Ad esempio, i valori k della distribuzione unilaterale dei limiti di tolleranza può essere ricavata dalla distribuzione normale a una coda. - Z1-P il valore di Z che lascia in una coda la proporzione 1-P o minore di dati, - Za il valore di Z per la probabilità a in una coda (i concetti di proporzione e probabilità in questo caso coincidono),
dapprima si stabilisce
con
Infine si calcola k con
Come esempio è utile seguire le indicazioni del manuale del dipartimento di ricerca della marina militare americana pubblicato nel 1960 (Statistical Manual by Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, Research Department U. S: Naval Ordnance Test Station, Dover Pubblications, Inc., New York, XVII + 288 p.).
Per una distribuzione
unilaterale il valore di
- per la proporzione P = 90% o maggiore è Z0.10 = 1,282 - per
una probabilità
In un
campione di dimensione
dopo aver calcolato
e
risulta
Si ottiene k =1,826 che risulta molto vicino al valore k = 1,838 riportato nella tabella specifica.
Per eliminare questa parte di calcolo, è riportata anche una tabella unilaterale per i valori k di uso più frequente, in campo biologico e ambientale, ripresa dal testo di Douglas C. Montgomery del 2001 Introduction to statistical quality control (4th ed., John Wiley Sons, Inc. XIX + 796 p.). Il termini relativi, la differenza tra i due valori è inferiore a 1%, più esattamente 0,67%. (forse imputabile al numero di decimali utilizzati nel calcolo).
ESEMPIO 2. (STIMA
DI UN INTERVALLO DI TOLLERANZA UNILATERALE). Su un campione con
Quale è la quantità minima presente in una proporzione del 90% alla probabilità del 5%.
Risposta. Dalla tabella dei valori k dei limiti di tolleranza a due code, per
è riportato k = 1,926. Da
si ottiene che il livello inferiore del limite di tolleranza è Li = 9,77 Con una probabilità non superiore al 5% di affermare il falso, almeno una proporzione del 90% del prodotto avrà una quantità di conservante superiore a 9,77 grammi.
Valori critici della distribuzione t di Student per un test bilaterale
Valori critici della distribuzione t di Student per un test unilaterale (prima parte)
Valori critici della distribuzione t di Student per un test unilaterale (seconda parte)
Confronto dei valori critici della distribuzione t tra un test bilaterale e un test unilaterale
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
di
dati, cioè l’intervallo di
confidenza o di fiducia, si usa
oppure
,
di un gruppo di
(riportato nelle
tabelle seguenti) è individuato da tre parametri:
(in una
distribuzione bilaterale) che l’affermazione sia vera,
CALCOLATI IN UN CAMPIONE DI
e
= 10,02 - 1,926 x 0,13 =
10,02 - 0,25 = 9,77
