INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

 

6.1.    DALLA POPOLAZIONE INFINITA AL CAMPIONE PICCOLO: LA DISTRIBUZIONE t DI STUDENT

 

 

Nella prassi della ricerca sperimentale, utilizzare un test di inferenza sulla media campionaria () conoscendo s², la varianza della popolazione, è un caso più teorico che reale. E’ una procedura possibile, ricorrendo a pubblicazioni o ad esperienze personali fondate su molti dati; ma per un ricercatore che raccoglie dati in natura o in laboratorio è un fatto poco frequente.

Quando la media della popolazione (m) non è nota, di norma anche la sua varianza () è ignota.

Di conseguenza, occorre utilizzare un sostituto della varianza della popolazione e la varianza del campione () ne rappresenta la stima più logica ed attendibile.

Con  ignota ed il ricorso all’uso di  in sua sostituzione, la distribuzione delle probabilità non è più fornita dalla distribuzione normale Z, ma da quella del t, detta t di Student, dallo pseudonimo di William Sealy Gosset (1876-1937).

Questo chimico inglese, allievo di Karl Pearson e collega di Fisher seppure non coetaneo (più vecchio di 14 anni), ebbe un'iniziale carriera accademica. Ma, in assenza di prospettive all’Università, dal 1907 prima andò a lavorare in una azienda, la birreria Guinness di Dublino, eseguendo analisi statistiche su campioni dei prodotti. Era una funzione simile a quello che oggi viene chiamato “controllo di qualità”. Usando campioni necessariamente ridotti per motivi economici e di praticità, studiò lo scarto tra le medie dei campioni estratti dalla stessa popolazione e la media dell'universo, in rapporto all'errore standard. Ne derivò una distribuzione che è diversa dalla normale, nel caso di piccoli campioni.

Nella sua situazione contrattuale, non poteva diffondere i risultati delle sue ricerche: i suoi datori di lavoro temevano che ciò potesse aiutare la concorrenza. Pubblicò ugualmente i suoi studi e descrisse le caratteristiche della nuova distribuzione in due articoli su Biometrika (la rivista fondata pochi anni prima da Karl Pearson (1857- 1936) e proseguita dal figlio Egon Sharpe Pearson (1896 - 1980) negli anni 1907 e 1908, ma firmandosi con un "nom de plume" o pseudonimo A. Student.

In testi di storia della statistica, in questa firma viene evidenziato un intento polemico: la soluzione del problema era stata raggiunta da uno studente (a student), un ricercatore che non avevano voluto come professore all’Università.

Quei suoi due lavori di Student rappresentano, storicamente, i fondamenti della distribuzione  t.

 

In realtà, Gosset chiamò la sua distribuzione Z.

Fu R. A. Fisher, intorno al 1925  e quindi quasi 20 anni dopo, che sviluppò questo metodo, la cui estensione a più gruppi e a situazioni sperimentali differenti porterà alla nascita e allo sviluppo dell’analisi della varianza.

In onore di Gosset e a ricordo delle sue pubblicazioni lo chiamò “t” di Student (nell’articolo Applications of “Student’s” distributions, pubblicato su Metron vol. 5, pp. 90-104). Ripropose questi concetti nella prima edizione del suo testo, Statistical Methods  for Research Workers (1^st ed. Oliver and Boyd, Edinburgh, Scotland, 239 pp. + 6 tables).

 

E' interessante evidenziare come nei primi vent’anni e fino al testo di Fisher tale scoperta di Student non fosse compresa, in particolare dal suo maestro Karl Pearson. Passare dal modello della distribuzione normale, formata da un gruppo di dati teoricamente infinito, a un modello di distribuzione che può essere applicato a campioni limitati, necessariamente formati da poche unità, era visto come una stravaganza, un’idea da cultura di basso rango, pure da parte del mondo accademico che stava ponendo le basi della statistica.

E’ quanto emerge dalla lettura dell’articolo postumo di Egon Sharpe Pearson del 1990 “Student”. A statistical Biography of William Sealy Gosset ( R. L. Plackett and G. A. Barnard eds., Clarendon Press, Oxford, England). A Gosset, che presentò le sue proposte e i suoi dubbi sui campioni piccoli, le idee che successivamente portarono allo sviluppo dei test  fondati sulla distribuzione t, il maestro Karl Pearson replicò (pag. 73) in termini sprezzanti : “Only naughty brewers deal in small samples”.

 

A questa impostazione molto più tardi rispose Ronald Aylmer Fisher (1890-1962), divenuto nel 1819 direttore del Rothamsted Agricultural Research Institute di Londra, il più importante centro di ricerche agrarie del Regno Unito. Nella prefazione della prima edizione del suo testo Statistical Methods  for Research Workers del 1925, il suo linguaggio è altrettanto deciso nel difendere l’approccio della ricerca applicata e nel condannare quella accademica, nel riproporre l’uso di campioni piccoli nei confronti della statistica fondata su popolazioni infinite di dati: “… the traditional machinery of statistical processes in wholly unsuited to the needs of practical research. Not only does it take a cannon to shoot a sparrow, but it misses the sparrow! The elaborate mechanism built on the theory of infinitely large samples is not accurate enought for simple laboratory data. Only by systematically tackling small sample problems on their merits does it seem possible to apply accurate tests to practical data”.

 

Nasce la statistica moderna.

Ha origine l’inferenza: la deduzione dal campione all’universo, lo studio di casi per conoscere le leggi della natura.

 

In una sperimentazione statistica elementare, nella quale si voglia ripetere l’esperienza di Gosset, la distribuzione t può essere ottenuta,

-  con un campione costante di dati (n),

-  analizzando le variazioni ottenute con il rapporto

 

t  =   =

 

Per una migliore comprensione dei concetti fondamentali di questo approccio e per una corretta applicazione dei test che ne sono derivati, è importante evidenziare le caratteristiche specifiche che differenziano questa distribuzione dalla gaussiana:

-  la distribuzione normale () considera solamente la variazione di campionamento della media  campionaria () rispetto a quella della popolazione (),

- la distribuzione t di Student tiene conto congiuntamente delle variazioni sia della media campionaria () sia della deviazione standard () calcolata sullo stesso campione di dati.

 

Per attuare una inferenza sulla media di una popolazione partendo da dati campionari, occorre pertanto considerare nello stesso tempo

-  sia la variazione di come stima di

-  sia la variazione di  come stima di .

 

All'aumentare del numero di dati campionari () le differenze si riducono poiché,

-   diventa una stima sempre migliore di .

Quando  è sufficientemente grande (teoricamente infinito, ma in pratica oltre 100; oppure, secondo altri testi più cautelativi o prudenziali, oltre 150 gdl),

-   e  s  hanno valori praticamente identici.

 

Nella ricerca applicata, i campioni raccolti in natura o in laboratorio con frequenza sono formati da poche osservazioni. In queste condizioni, la differenza tra il valore del t di Student e il corrispondente valore di Z alla stessa probabilità a è rilevante.

 

 

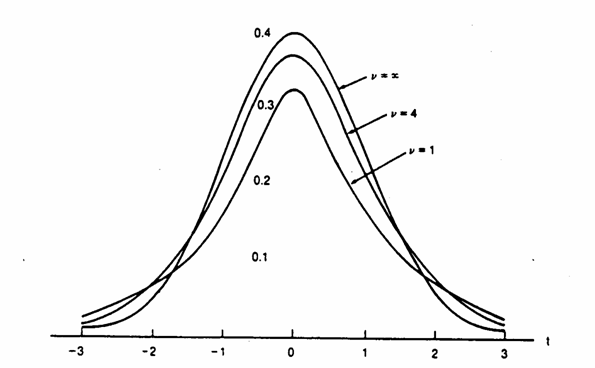
Distribuzione normale standardizzata

CORRISPONDENTE ALLA DISTRIBUZiONE t DI STUDENT CON GDL n = ¥

e distribuzione t di Student per 4 E 1 gradi di libertà (n = 4  e n = 1).

 

 

La rappresentazione grafica della curva t di Student mostra le sue caratteristiche di distribuzione di probabilità teoriche.

La sua forma

-  è simmetrica e a campana come la normale,

-  ma con una dispersione maggiore, quanto minore è il numero di gradi di libertà.

Le diverse curve e le tabelle della distribuzione t (riportate alla fine del capitolo) evidenziano che

-  non vi è una sola curva t ma, a differenza di quanto avviene per la gaussiana

- esiste una intera famiglia di distribuzioni t, una per ogni grado di libertà.

 

Dovrebbero quindi essere pubblicati interi volumi di tabelle dei suoi valori critici. In realtà, come già visto per il chi quadrato, anche per la distribuzione t abitualmente si utilizza una sola tavola sinottica, una pagina ordinata di sintesi, che riporta i valori critici più importanti.

Alla fine del capitolo, per favorire la comprensione dei concetti e la stima delle probabilità, sono state riportate 3 differenti tabelle:

-  la prima è per un test bilaterale,

-  la seconda è per un test unilaterale,

-  la terza  permette un confronto rapido tra le probabilità associate ai due casi.

Il modo di lettura delle tre tabelle è identico:

-  la parte superiore di ogni colonna indica l'area sottesa nelle rispettive code della distribuzione,

-  mentre ogni riga fa riferimento ad uno specifico grado di libertà, riportato nella prima colonna.

 

I valori critici

-  per l'area in una coda alla probabilità  coincidono con quelli della probabilità  nella distribuzione a due code;

-  viceversa, quelli associati alla probabilità  in due code coincidono con i valori associati alla probabilità  nella distribuzione a una coda.

 

Per esempio, confrontando le rispettive tabelle si osserva che

-   con 10 gdl in un test ad una coda per = 0.05 il valore critico t =  1,8125;

-  sempre con 10 gdl ma per un test a due code, per  = 0.05 il valore critico è t = 2,634;

-  nella distribuzione ad una coda, i valori di t per  = 0.05 coincidono con quelli riportati nella colonna di  = 0.10 della distribuzione a due code;

- inversamente, i valori per  = 0.05 nella tabella per test a due code coincidono con la colonna dei valori di a = 0.025 nella tabella per test ad una coda.

 

Quando la distribuzione t di Student è applicata a test di verifica delle ipotesi, è necessario rispettare le condizioni di validità. Poiché essa è derivata direttamente dalla normale, occorre rispettare le condizioni richieste per i test parametrici (media e varianza sono detti i parametri della distribuzione normale)

E' condizione di validità della distribuzione t di Student, e quindi dei test che la utilizzano,

- -  che la distribuzione dei dati sia normale e

- - che le osservazioni siano raccolte in modo indipendente.

La seconda condizione dipende dalla modalità di organizzazione della raccolta dei dati. Ad esempio, le osservazioni non sono indipendenti se entro un gruppo di persone delle quali si misura il peso esistono più fratelli; se, in un esperimento sulla conducibilità elettrica di un metallo a temperature diverse, si utilizzano campioni di metallo diversi ma un campione è misurato più volte.

Rispetto alla condizione di normalità la distribuzione t è robusta. Con tale termine tecnico si intende affermare che rimane approssimativamente valida, anche quando le distribuzioni di dati non rispettano esattamente la condizione dalla normalità.

 

Nella statistica applicata, il test t è utilizzato in quattro casi: per il confronto tra

1 - la media di un campione e la media dell’universo o una generica media attesa;

2 – un singolo dato e la media di un campione, per verificare se possono appartenere alla stessa popolazione;

3 - la media delle differenze di due campioni dipendenti con una differenza attesa;

4 - le medie di due campioni indipendenti.

 

Per ognuno dei tre casi sulle medie

-  media di un campione,

-  media delle differenze tra due campioni dipendenti,

-  differenza tra le medie di due campioni indipendenti,

è possibile calcolare l’intervallo di confidenza.

Come già visto con la distribuzione Z, con esso si può conoscere l’intervallo entro il quale è collocato il valore reale della popolazione alla probabilità a, partendo dalla misura campionaria.

Inoltre, il metodo dell’intervallo di confidenza rappresenta un’alternativa ai test d’inferenza bilaterali.

 

Come emergerà più volte nel testo, le distribuzioni fondamentali della statistica sono 4 :

-  la distribuzione normale ,

-  la distribuzione  di Student,

-  la distribuzione  di Fisher,

-  la distribuzione  di Pearson.

Per la stessa probabilità a, esiste

 la relazione

 dove

-   = valore di  alla probabilità  in una distribuzione bilaterale;

-   = valore di  alla probabilità  in una distribuzione bilaterale, per gradi di libertà infiniti;

-   = valore di  alla probabilità , per gradi di libertà 1 al numeratore e infiniti al denominatore;

-   = valore di  alla probabilità , per 1 grado di libertà.