|
INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT
6.2. CONFRONTO TRA UNA MEDIA OSSERVATA E UNA MEDIA ATTESA,
CON CALCOLO DEI LIMITI DI CONFIDENZA DI UNA MEDIA, CON
La distribuzione t con n-1 gdl (indicata con tn-1) è data dal rapporto - tra la
differenza della media campionaria - con il suo
errore standard s/ come espresso dalla formula
t(n-1) =
dove - -
E’ importante ricordare che, come ampiamente presentato nel capitolo sulla statistica descrittiva, la deviazione standard è ottenuta a partire dalla devianza mediante la formula
dove la parte sotto radice è chiamata varianza campionaria corretta o stima corretta della varianza.
Ai fini pratici del calcolo, la devianza
è stimata più rapidamente e con maggiore precisione, in quanto non prevede arrotondamenti caratteristici delle medie, ricorrendo alla formula abbreviata
Per verificare l’ipotesi relativa alla
media - l'ipotesi alternativa H1 è scritta come H1 : m ¹ m0 - e l’ipotesi nulla H0 H0: m = m0 dove - m è la media della popolazione da cui è
estratto il campione con media osservata - m0 è la media attesa o di riferimento per il confronto.
Con la medesima simbologia, in un test unilaterale - l'ipotesi alternativa H1 è scritta come H1 : m < m0 - e l’ipotesi nulla H0 corrispondente H0: m ³ m0 al fine di verificare se la media del campione è significativamente minore della media attesa (con formulazione più estesa e precisa, se la media della popolazione dalla quale è stato estratto il campione è minore della media attesa) oppure nelle direzione opposta l’ipotesi nulla H0 è scritta come H0: m £ m0 e l'ipotesi alternativa H1 come H1 : m > m0 al fine di verificare se la media della popolazione m da cui è estratto il campione è maggiore di quella attesa m0.
Dalla precedente formula da utilizzare per verificare la differenza tra media campionaria e media attesa t(n-1) =
si può derivare
quella dell'intervallo di confidenza (confidence interval,
tradotto spesso anche intervallo fiduciale), entro il quale alla
probabilità a è compresa la media reale Lo sviluppo dei concetti di intervallo di confidenza, che è applicato a diverse misure (varianza, coefficiente angolare nella retta, ecc.…) e non solo alla media come in questo caso, è attribuito a Jerzy Neyman per averlo introdotto nel 1934 con i termini confidence interval o confidence coefficient, benché il concetto fosse già stato proposto un secolo prima. In varie situazioni come in questo testo, si usa come sinonimo benché non lo sia in tutte le situazioni, anche il termine fiducial interval sviluppato da R. A. Fisher nel 1930 (per ulteriori chiarimenti vedi di J. Pfanzagl del 1978 Estimation: Confidence interval and regions, pp. 259-267 in Kruskal and Tanur). La formula per il calcolo dell’intervallo di confidenza diventa
dove Sommando alla media campionaria le due parti, la quota positiva e quella negativa, si ottiene l'intervallo che comprende la media con probabilità a prefissata
ESEMPIO 1. In un appezzamento di terreno adibito a vivaio, sono coltivate pianticelle della specie A; una lunga serie di misure ha dimostrato che dopo due mesi dalla semina raggiungono un’altezza media di 25 centimetri. A causa di un incidente, su quel terreno sono state disperse sostanze tossiche; si ritiene che esse incidano negativamente sulla crescita di alcune specie, tra le quali la specie A. Per una verifica di tale ipotesi, vengono seminate sul terreno inquinato 7 pianticelle che, controllate dopo 2 mesi, raggiungono le seguenti altezze in cm.: 22, 25, 21, 23, 24, 25, 21. Si intende rispondere a due quesiti. 1 - Si può sostenere che le sostanze tossiche disperse inibiscano la crescita della specie A? 2 - Quale è la media reale dell’altezza delle piante dell’età di due mesi, nella nuova condizione del terreno?
Risposta 1. E’ un test ad una coda in cui l’ipotesi nulla è H0 : m ³ m0 e l’ipotesi alternativa è H1 : m < m0 Infatti, se le sostanze tossiche inibiscono la crescita, la media m della popolazione da cui è estratto il campione di 7 piante può solo essere inferiore alla media m0 della popolazione precedente pari a 25. Il test assume
significato solamente se la media campionaria Scegliendo una probabilità a = 0.05 e applicando la formula t(n-1) =
dove, sulla base dei 7 dati campionari,
si ottiene un valore t(6) = di t con 6 gdl uguale a - 3,05. Il segno negativo indica solamente che la differenza è negativa rispetto al valore atteso; ai fini della significatività, il valore di t viene preso in modulo. Per un test ad una coda, il valore critico del t alla probabilità 0.05 con 6 gdl è uguale a 1,943. Il valore calcolato in modulo è superiore a quello riportato nella tabella sinottica della distribuzione t. Pertanto, con probabilità inferiore a 0.05 (di commettere un errore) si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa: le sostanze tossiche disperse inibiscono la crescita delle piante della specie A in modo significativo.
Risposta 2. L’altezza media reale m della popolazione dalla quale sono stati estratti i 7 dati può essere stimata mediante l’intervallo di confidenza
Con i dati del campione
e il valore del t associato alla
probabilità 0.05 per un test a due code con 6 gdl si calcola che
Pertanto, alla probabilità complessiva a = 0.05 - il limite inferiore l1 ed il limite superiore l2 dell’intervallo di confidenza risultano rispettivamente:
In questo caso, non è possibile il confronto diretto tra le due risposte poiché - nella prima è un test unilaterale (con t(0.05, 6) = 1,943), - mentre nella seconda l’intervallo di confidenza utilizza il valore di t corrispondente a un test bilaterale (con t(0.025,6) = 2,447).
Esempio 2. Disponendo di un campione di 13 individui di Heterocypris incongruens pescati in un fiume, dei quali sono riportate le lunghezze (in mm),
si vuole verificare se alla probabilità P = 0.99 la loro lunghezza media è significativamente differente dalla media di 1,25 mm stimata per la stessa specie nei laghi della regione, in varie ricerche precedenti.
Risposta. E’ possibile fornire una risposta sia mediante l’applicazione del test t per un campione (1), sia attraverso la stima dell’intervallo di confidenza della media campionaria (2).
1 - Dai 13 dati campionari, devono essere calcolati il valore della media e della deviazione standard:
La domanda dell’esempio richiede un test a due code o bilaterale, poiché prima della raccolta dei dati è ugualmente logico che la media del campione abbia un valore sia significativamente minore sia maggiore della media attesa. Indicando con m la media reale del campione estratto dal fiume e con m0 la media della popolazione che vive nei laghi, l’ipotesi nulla è H0 : m = m0 e l’ipotesi alternativa H1 : m ¹ m0
Mediante il test t t(12) =
si ottiene un valore di t(12) uguale a -0,917. Alla probabilità a = 0.01 per un test bilaterale con 12 gdl il valore critico riportato è uguale a 3,055. Il valore calcolato in modulo è nettamente inferiore a quello corrispondente riportato nella tavola sinottica; di conseguenza, non si è in grado di rifiutare l’ipotesi nulla. La dimensione media dei 13 individui della specie Heterocypris incongruens pescati nel fiume non è significativamente diversa da quella degli individui della stessa specie che vivono nei laghi della regione.
2 - Per la stima dell’intervallo di confidenza, dopo il calcolo dei medesimi parametri si deve scegliere il valore del t con 12 gdl - alla probabilità a = 0.01 per un test a due code oppure - alla probabilità a= 0.005 per un test a una coda trovando in entrambi i casi t0.005; 12 = 3,055. I valori del limite inferiore l1 e del limite superiore l2 dell’intervallo fiduciale
risultano rispettivamente La media della popolazione m0 uguale a 1,25 è compresa nell’intervallo fiduciale della media campionaria. Pertanto, non esiste una differenza significativa alla probabilità prefissata di a = 0.01 in un test bilaterale.
Si può osservare come questo risultato coincida con quello ottenuto nella prima parte della risposta: il valore atteso m0, risulta non significativamente differente dal valore della media campionaria; pertanto alla stessa probabilità a risulta compreso nel suo intervallo fiduciale. Se fosse stata rifiutata l’ipotesi nulla, il valore atteso risulterebbe escluso dall’intervallo fiduciale calcolato.
Con un numero maggiore di osservazioni, la differenza facilmente sarebbe risultata significativa. Per la stima del numero di dati utili, è importante osservare che - un aumento del numero di dati campionari agisce doppiamente sulla riduzione dell'intervallo di confidenza e sulla significatività del t: - attraverso il valore del t(n-1), che diminuisce al crescere di gdl, - mediante la
riduzione dell'errore standard, come evidenzia il rapporto
| |||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
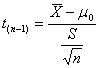
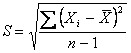
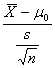
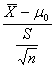
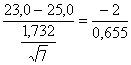 = -3,053
= -3,053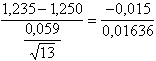 = -0,917
= -0,917