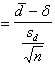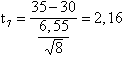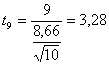INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

 

6.5.  IL TEST t PER 2 CAMPIONI DIPENDENTI O PER DATI APPAIATI CON INTERVALLO DI CONFIDENZA DELLA MEDIA DELLE DIFFERENZE

 

 

Caratteristica distintiva del confronto tra 2 campioni dipendenti è poter accoppiare ogni osservazione di un campione con una e una sola osservazione dell'altro campione; necessariamente, i due gruppi hanno sempre lo stesso numero di dati. Le tecniche sono tre:

1 – dati auto-appaiati,

2 – dati naturalmente appaiati,

3 – dati artificialmente appaiati.

 

1 - La situazione più semplice è quella dell'auto-accoppiamento, in cui ogni soggetto serve come controllo di se stesso; si parla anche di dati auto-appaiati e si confrontano i valori presi sugli stessi soggetti in 2 momenti diversi.

Un esempio classico è la comparazione tra i livelli di inquinamento rilevati

- nello stesso gruppo di località in due momenti differenti,

 al fine di verificare se vi siano state in media variazioni significative; oppure prima e dopo interventi di risanamento, al fine di valutare la loro efficacia.

In medicina e in ecotossicologia si parla di autoappaiamento dei dati quando gli stessi individui sono misurati prima e dopo l’intervento, appunto per valutarne l’efficacia.

 

2 - Tuttavia questa tecnica non sempre è possibile: se si deve analizzare l’effetto di due sostanze tossiche, l’effetto di due interventi chirurgici su cavie non è possibile somministrale entrambe agli stessi individui, ma è necessario formare due gruppi distinti, cercando di fare in modo che gli individui che li compongono siano tra loro simili a coppie.

E’ la seconda situazione, quando le osservazioni nei due gruppi sono naturalmente appaiate: le misure non sono tratte dagli stessi individui, ma sono effettuate su coppie di individui scelti appositamente.

E' il caso in cui, per esaminare l’effetto di due tossici, si deve avere a disposizione alcune nidiate per scegliere coppie di animali, entro ognuna. Ovviamente, i due individui della coppia sono uguali per età e hanno gli stessi genitori; inoltre possono essere scelti dello stesso sesso, delle stesse dimensioni o qualsiasi altro parametro utile al confronto nel caso specifico. Il primo individuo della coppia viene assegnato casualmente ad un gruppo ed il secondo all’altro gruppo. Nella scelta degli individui dalla nidiata e nell’attribuzione al gruppo può essere presente un certo grado di soggettività, che tuttavia è in gran parte eliminata con la scelta casuale, la randomizzazione, effettuata mediante l’estrazione di numeri casuali.

Un altro esempio di dati naturalmente appaiati può essere tratto da esperimenti di etologia, con il confronto nella cura dei figli tra il comportamento della madre e quello del padre, ovviamente riferiti agli stessi cuccioli.

 

3 - La terza situazione è l'appaiamento artificiale, un procedimento relativamente frequente nella ricerca ambientale. Si supponga di avere alcuni laghi con un tasso elevato d’inquinamento e di non avere raccolto da essi misure in condizioni normali o standard. Per ogni lago inquinato è possibile cercare un lago non inquinato (relativamente simile per vicinanza fisica, altezza sul livello del mare, configurazione del terreno e per altri vari fattori), che si presume possa essere rappresentativo del corrispondente prima dell’inquinamento. Le differenze nel parametro rilevato tra i tassi di ogni coppia di laghi diviene una stima dell’effetto dell’inquinamento. E’ ovvio che ricercatori differenti potrebbero scegliere coppie di laghi diverse, pure agendo nelle stesse condizioni sperimentali.

E’ una procedura in cui la componente di soggettività è  molto elevata.

 

Scopo principale della tecnica di appaiamento dei dati è determinare

-  il massimo di omogeneità entro ogni coppia e

-  il massimo di eterogeneità tra le coppie.

Il confronto tra trattamento e controllo, fatto su gli stessi individui o tra situazioni simili, tenta di eliminare alcune sorgenti di variabilità che potrebbero essere in grado di nascondere le reali differenze tra le due serie di misure: l'obiettivo è di esaminare le differenze fra due misurazioni, dopo aver ridotto l'effetto della variabilità dovuta agli elementi o individui, poiché sono gli stessi che compongono i due gruppi.

Ad esempio, scegliendo dalla stessa nidiata due cavie dello stesso sesso, si elimina l’eventuale differenza degli effetti di una sostanza tossica nei due sessi o in individui di età diversa.

 

Tecnicamente il confronto tra le medie di 2 serie di osservazioni appaiate è semplice: l'analisi è applicata ad una nuova serie di dati, quelli risultanti dalle differenze tra gli elementi di ciascuna coppia.

Per il test t di Student, nel caso di un test bilaterale l'ipotesi nulla H₀ è che la media dell'universo delle differenze sia uguale a 0

H₀: d = 0

 mentre l'ipotesi alternativa H₁ è

H₁: d  0

 

In un test unilaterale, l'ipotesi nulla H₀ è che la media dell'universo delle differenze sia maggiore o uguale a 0

H₀: d  ³ 0

 mentre l'ipotesi alternativa H₁ afferma che la differenza è minore della quantità prefissata (spesso 0); può essere scritta come

H₁: d < 0

 

Nel caso opposto, l'ipotesi nulla H₀ è che la media dell'universo delle differenze sia minore o uguale a 0

H₀: d  £ 0

 mentre l'ipotesi alternativa H₁ afferma che la differenza è maggiore della quantità prefissata (spesso 0); può essere scritta come

H₁: d > 0

 

Per la scelta tra l’ipotesi nulla H₀ e l’ipotesi alternativa H₁, formulata a priori, la significatività della media delle differenze è verificata con il rapporto

 

t_(n-1) 

dove

-      è la media della colonna delle differenze;

-   d    è la differenza media attesa: spesso, ma non necessariamente, è uguale a 0;

-   s_d     è la deviazione standard calcolata sulla colonna delle differenze;

-   n    è il numero di differenze, corrispondente anche al numero di coppie di dati.

 

L’intervallo di confidenza della media delle differenze  tra i due campioni dipendenti, entro il quale alla probabilità a è compresa la media reale   delle differenze, con la medesima simbologia della formula precedente,

 è calcolato mediante

 dove  

  indica il valore della distribuzione t con n-1 gradi di libertà alla probabilità  .

 

ESEMPIO 1. Un programma di disinquinamento, applicato sui dati di una regione, ha abbassato la presenza di sostanze inquinanti di 30 punti. Su 8 laghi è stata applicata una procedura differente; di questi ultimi sono riportati i valori d’inquinamento prima e dopo l’intervento:

 

 

 

Ai fini di una valutazione dei risultati è necessario rispondere a due quesiti:

1- Il secondo programma di disinquinamento è significativamente migliore del primo?

2 - Quale è il reale valore di abbattimento del tasso di inquinamento alla probabilità a = 0.05?

 

Risposta 1.   E’ un test ad una coda, dove

-  l’ipotesi nulla H₀ assume che la media  delle differenze tra le coppie di dati non è significativamente maggiore della precedente, che era risultata uguale a +30;

H₀ :  d  =  30

-  l’ipotesi alternativa H₁ è unilaterale: afferma che la media delle differenze tra prima e dopo l’intervento negli 8 laghi sia significativamente maggiore di 30, la media della sperimentazione precedente.

H₁ : d  >  30

Per l’applicazione del test t di Student nel caso di due campioni dipendenti, dapprima si deve calcolare la colonna delle differenze (d) tra coppie di dati campionari (riportati in grassetto nella tabella sottostante).

Per tutti i calcoli successivi si utilizzano solamente questi valori, ignorando i dati originali rilevati prima e dopo gli interventi; in questo modo, si elimina l’effetto di avere laghi che hanno livelli medi (tra prima e dopo) d’inquinamento diversi.

 

Lago	Prima	Dopo	D
A	180	140	40
B	175	145	30
C	165	140	25
D	195	160	35
E	180	150	30
F	180	145	35
G	200	160	40
H	190	145	45

 

 

Dalla colonna delle differenze (d), si stimano

-  la media  

-  la devianza s_d 

 ottenendo i valori:

 necessari per calcolare un t con 7 gdl,

 

Il risultato è uguale a 2,16.

Nella tavola sinottica, il valore critico di t

-  con 7 gdl e  per un test ad una coda

- alla probabilità a = 0.05  è uguale a 1,895.

 

Il valore calcolato (2,16) è superiore a quello tabulato: la probabilità P che questa differenza tra media osservata e media attesa sia dovuta al caso è inferiore a 0.05. Di conseguenza, si rifiuta l'ipotesi nulla H₀ e si accetta l'ipotesi alternativa H₁.

Il nuovo metodo di disinquinamento è più efficace del precedente: abbatte i valori d’inquinamento di una quantità significativamente superiore a 30 punti.

 

Risposta 2. Per conoscere la media reale (d) di riduzione della presenza di liquami con il secondo esperimento, si deve calcolare l’intervallo fiduciale della media delle differenze associato alla probabilità a = 0.05.

Applicando alla formula generale

 i dati delle differenze campionarie già stimate

 ed utilizzando il valore di t_{(0.025, 7)} = 2,365

si ottiene un intervallo

d = 35 ± 2,365 ×    =   35 ± 5,485

in cui

-  il limite inferiore è l₁ = 29,515

-  il limite superiore è l₂ = 40,485.

La media reale (d) di abbattimento dei liquami con il secondo processo alla probabilità a = 0.05 varia da 29,515 e 40.485. Il valore di 30 è compreso in questo intervallo. Quindi, in un test bilaterale associato alla probabilità a = 0.05 non si sarebbe rifiutata l’ipotesi nulla.

E’ utile porre attenzione al fatto che questo risultato non coincide esattamente con quello precedente, poiché l’intervallo di confidenza è sempre bilaterale, mentre il test precedente era unilaterale. Prima è stato possibile dimostrare un miglioramento significativo, solo perché il test t verificava un’ipotesi alternativa H₁ ad una coda, che è più potente del corrispondente test bilaterale.

 

ESEMPIO 2.   Si vuole verificare se un conservante per alimentazione umana abbia effetti sui fattori di crescita. A questo scopo, un gruppo di 10 cavie adulte è stato sottoposto a un regime di alimentazione contenente la sostanza da testare.

Ogni soggetto è stato pesato sia prima che dopo la nuova dieta, per misurarne le variazioni.

Nella tabella sottostante sono riportati i pesi in grammi prima e dopo la dieta, per ognuna delle 10 cavie:

 

 

Si vuole sapere:

1 - Se la sostanza può essere la causa di variazioni significative di peso.

2 - Quale è la reale variazione (d) di peso determinata dal conservante, alla probabilità a = 0.05.

 

Risposta 1.   E’ un test bilaterale, in cui (come sempre)

- l’ipotesi nulla H₀ afferma che la media reale (d) delle differenze (d) è uguale a 0

H₀: d = 0

 

- mentre l’ipotesi alternativa H₁ afferma che è diverso da 0:

H₁: d ¹ 0

Dalla colonna delle differenze (D) tra le 10 coppie di valori osservati

 

 

 

 si calcolano

-  la somma delle D che risulta uguale a +90 e

-  la somma delle (d - )²  (cioè la devianza) che risulta uguale a 676.

Da esse, si ricavano

-  la media (),

-  la deviazione standard (s_d)

 

-  il numero di coppie di osservazioni (n) o di differenze sulle quali sono stati effettuati i calcoli

n = 10

Infine si stima

 un valore di t con 9 gdl uguale a 3,28.

 

Per un test a due code, il valore critico della distribuzione t per 9 gdl e d  = 0.05 è uguale a 2,262.

Il valore calcolato (3,28) è superiore: la probabilità P che la differenza riscontrata sia dovuta al caso è minore di 0.05.

Si rifiuta l'ipotesi nulla H₀ e si accetta l'ipotesi alternativa H₁: la nuova dieta determina nelle cavie una differenza ponderale che è significativa.

 

Risposta 2.   Il valore reale (d) della differenza è ottenuto mediante la stima dell'intervallo fiduciale della differenza media, che per due campioni dipendenti è dato da

 

 

Con i dati dell'esercizio,

-  per la probabilità a = 0.05 alla quale corrisponde

-  un valore con t_0.025 in entrambe le code o t_0.05 bilaterale uguale a 2,262

 si ottiene

d =

 dalla quale risulta un intervallo

d₁ = -2,81     e    d₂ = -15,19

 

La nuova dieta alla quale sono state sottoposte le cavie determina una riduzione media (d) di peso uguale a 9; alla probabilità a = 0.05  essa ha come valori estremi - 3,81 e -15,19. Si può osservare che il valore di d espresso nell'ipotesi nulla () è escluso dall'intervallo fiduciale calcolato; quindi si discosta dal valore medio sperimentale in modo significativo alla probabilità prescelta.

In un test a due code, alla medesima probabilità con cui nel test t per dati appaiati la differenza media risulta significativa, il valore dell'ipotesi nulla è escluso dall'intervallo fiduciale.

Per quanto riguarda la significatività, i due approcci forniscono la medesima informazione.

 

Secondo vari autori di testi di statistica applicata, quando il numero di coppie di dati appaiati è superiore a 40 (altri indicano 50 o addirittura 150), la distribuzione t di Student è approssimata in modo sufficiente dalla distribuzione normale standardizzata Z. Confrontando i valori riportati nelle tabelle, si può infatti osservare che alla probabilità a = 0.05 il valore critico di t (uguale rispettivamente a 2,02 per 40 gdl e 2,01 per 50 gdl) si discosta di una quantità trascurabile (circa il 2% in percentuale) dal corrispondente valore di Z (uguale a 1,96).

Nella formula per il calcolo della varianza, con una differenza di risultati che da molti ricercatori è ritenuta trascurabile, quando n è di alcune decine è possibile sostituire il valore critico di t con il valore di Z associato alla probabilità a prefissata, sia in test ad una coda che in test a due code.

 

Di conseguenza,

- il test Z per la significatività della media diventa

 

Z 

 

- l’intervallo fiduciale è stimato con