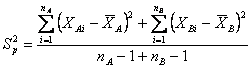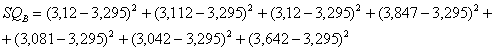INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

 

6.7.   IL TEST t PER 2 CAMPIONI INDIPENDENTI O PER DATI NON APPAIATI

 

 

In molti casi, non è tecnicamente possibile formare due campioni dipendenti. Spesso non è possibile misurare gli effetti di due differenti trattamenti sugli stessi individui: è il caso in cui si confrontano misure di accrescimento somatico in animali o piante sottoposte a condizioni ambientali differenti oppure si confrontano livelli d’inquinamento idrico tra due fiumi differenti con rilevazioni in varie stazioni. Altre volte, non è possibile nemmeno fare appaiamenti naturali o artificiali, perché le situazioni non si ripetono a coppie nelle medesime condizioni e la dose di soggettività è ritenuta eccessiva.

L'unica possibile strategia di analisi dei dati è quella di confrontare due campioni indipendenti, due campioni formati da individui differenti. Aumenta la variabilità tra i due gruppi: nel caso di cavie, in uno possono essere presenti più maschi o più femmine, più individui anziani o più giovani, più sani o ammalati, per cui la variabilità delle risposte aumenta. Ma si ottengono due vantaggi:

-  poter utilizzare un numero differente di osservazioni,

-  avere dati che più facilmente sono espressione della variabilità casuale,

-  utilizzare per il confronto con il proprio un campione raccolto da altri.

 

Con il test di significatività per due campioni indipendenti, viene verificata la stessa ipotesi del caso di dati appaiati, seppure espressa in forma diversa. E' infatti fondamentale comprendere che

-  per due campioni dipendenti i calcoli vengono effettuati sulla sola colonna delle differenze, mentre

-  nel caso di due campioni indipendenti i calcoli vengono effettuati sulle due serie di osservazioni.

In un test a due code o bilaterale, l'ipotesi nulla H₀ è che i due campioni (indicati con A e B) siano estratti dalla stessa popolazione oppure da due popolazioni differenti ma con media (m) uguale; essa può essere scritta come

H₀: m_A = m_B      oppure      H₀: m_A - m_B  = 0

 

  e  la sua ipotesi alternativa H₁ come

H₁:  m_A ¹ m_B       oppure        H₁:  m_A - m_B ¹ 0

 

In un test ad una coda o unilaterale  si possono avere due impostazioni alternative:

 

-  in un caso, l’ipotesi nulla può essere

H₀: m_A £ m_B      oppure      H₀: m_A - m_B  £ 0

 contro l’ipotesi alternativa

H₁:  m_A > m_B       oppure        H₁:  m_A - m_B > 0

 

-  nell’altro caso l’ipotesi nulla può essere

H₀: m_A ³ m_B      oppure      H₀: m_A - m_B  ³ 0

 contro l’ipotesi alternativa

H₁:  m_A < m_B       oppure        H₁:  m_A - m_B < 0

 

Nel caso di 2 campioni indipendenti, i gradi di libertà del t sono uguali a (n_A–1) + (n_B-1), che possono anche essere scritti come (n_A + n_B - 2) oppure (N-2).

Il valore del t è ottenuto mediante

 dove

-   e    sono le medie rispettivamente del campione A e del campione B,

-  m_A e  m_B  sono le rispettive medie attese, espresse nell’ipotesi nulla,

-  n_A e n_B   sono il numero di osservazioni nei campioni A e B,

-   è la varianza associata (pooled) dei due gruppi a confronto,

-  N = n_A + n_B

 

La varianza associata o varianza pooled (s²_p) è data dal rapporto tra la somma delle due devianze e la somma dei rispettivi gradi di libertà

 

 

dove

-    e    sono nell’ordine i dati e la media del gruppo A,

-    e    sono rispettivamente i dati e la media del gruppo B,

-    sono il numero di osservazioni nei campioni A  e  B.

La varianza pooled è una varianza media ponderata, calcolata sempre a partire dalle due devianze e dai loro gdl, che attribuisce una importanza proporzionalmente maggiore al gruppo che ha un numero maggiore di dati.

 

Nella ricerca biologica, medica e ambientale, ricorre con relativa frequenza il caso in cui si debbono confrontare i risultati di due ricercatori diversi (indicati con A  e  B), ognuno dei quali ha pubblicato solo i tre valori fondamentali dei suoi dati:

-  la media campionaria ,

-  una misura della variabilità, quali varianza (S²) o deviazione standard (S) o errore standard (es),

-  numero di dati raccolti (n).

Per verificare se tra le due medie campionarie esiste differenza, è possibile utilizzare il test t con la solita formula

dopo aver calcolato la varianza pooled ().

Come risulta dalla formula precedente,

 

occorre ritornare alla devianza

di ognuno dei due gruppi.

A questo scopo è utile ricordare che

-  se si dispone della varianza S²  oppure delle deviazione standard (S)

 si ottiene la devianza attraverso la relazione

 

-  mentre se si dispone dell’errore standard (es)

 si ottiene la devianza attraverso la relazione

 

ESEMPIO. Si intende verificare due gruppi del Cladocero Daphnia magna (del quale sono stati misurati 5 individui per il campione 1 e 7 individui per il campione 2, come riportato nella tabella sottostante) dopo 20 giorni dalla schiusa delle uova hanno raggiunto dimensioni medie significativamente differenti.

 

 

 

Risposta.  E’ un test bilaterale, in cui

H₀: m_A = m_B     e     H₁: m_A ¹ m_B

Dopo aver calcolato

- la media del gruppo X_A

 

- la media del gruppo X_B

 

- la devianza del gruppo A (SQ_A)

 

- la devianza del gruppo B (SQ_B)

 

 si stima

- la varianza associata ()

 

Con   n_A = 5  e   n_B = 7

 si calcola il valore di t con 10 gdl

 

 che risulta uguale a 4,26.

Poiché il valore di t con 10 gdl per un test bilaterale (vedi tabella relativa alla fine del capitolo)

-  alla probabilità a = 0.05 è uguale a 2,228

-  alla probabilità a = 0.01 è uguale a 3,169

-  alla probabilità a = 0.001 è uguale a 4,587

 si rifiuta l’ipotesi nulla, con probabilità inferiore a 0.01 di commettere un errore di I Tipo (rifiutare l’ipotesi nulla quando essa è vera). Pertanto, si deve concludere che la differenza tra le medie dei due campioni risulta molto significativa.

 

Per ognuno dei due campioni, i dati possono essere riassunti in una tabella come la seguente

 

 

 

 

In realtà, oltre al numero di dati raccolti e alla media, è sufficiente riportare una sola coppia di valori delle ultime 3 (varianza, deviazione standard, errore standard), potendo da una qualsiasi di esse ricavare le altre due, quando appunto si conoscano le dimensioni del campione (n) oppure i suoi gdl (n-1).

 

Per valutare la significatività della differenza tra le due medie, sempre con un test bilaterale in cui

H₀: m_A = m_B     e     H₁: m_A ¹ m_B

prima di tutto è necessario ricavare la devianza (SQ) di ognuno dei due campioni:

-  dalla varianza S²

 

                         

 

-  dalla deviazione standard S

 

                    

 

-  dall’errore standard es

 

                    

 

 si perviene sempre alle stesse stime delle due devianze (SQ_A = 0,1595  e  SQ_B = 0,6246) a meno delle approssimazioni utilizzate nei calcoli.

Da esse si ricava la varianza associata

 

 e quindi il valore del t

 

 

 che ovviamente è uguale a quello calcolato in precedenza, utilizzando i singoli dati.