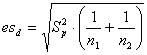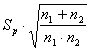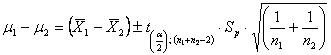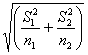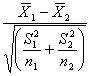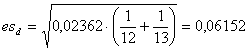INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

 

6.9.   SIGNIFICATIVITA’ E INTERVALLO DI CONFIDENZA DI UNA DIFFERENZA

 

 

Se le varianze risultano statisticamente differenti, si può utilizzare il test t solo dopo adeguata trasformazione dei dati originali (che sarà discussa alla fine dei capitoli sull’analisi della varianza). Con la trasformazione dei dati,

-  le medie devono rimanere differenti mentre le varianze devono diventare uguali.

Se le varianze dei due gruppi a confronto restano significativamente differenti, si deve ricorrere a un test di statistica non parametrica per 2 campioni indipendenti.

 

Le stesse condizioni sono richieste per

- l'intervallo fiduciale della differenza tra le 2 medie campionarie .

Il metodo è simile al test t di Student per due campioni dipendenti, ricordando che

-  i gdl di t sono (n₁-1) + (n₂-1) (scritti anche come n₁ + n₂ -2)

- e soprattutto che l'errore standard della differenza (es_d )

 è

 

L’errore standard della differenza tra due campioni indipendenti può essere calcolata anche

 mediante

es_d =

 

Per calcolare l'intervallo fiduciale della differenza tra due medie con varianze uguali

si applica la formula

 

 

Quando le due varianze non sono omogenee, si può calcolare

- l’errore standard della differenza (es_d)

 

es_d =

-  il valore d con

 

d =

 

 che è una deviata normale standardizzata, quando n₁ e n₂ sono abbastanza grandi.

-  l'intervallo fiduciale con

 

m₁  - m₂ = 

 

Quando n₁ e n₂ sono piccoli si deve ricorrere ad altre soluzioni,

-  come il metodo proposto da Welch oppure quello di Behrens (discusso in modo approfondito in un paragrafo successivo),

-  intervalli di confidenza non parametrici.

 

L’ultima formula riportata

d =

 

nella parte che considera l’errore standard evidenzia che

-  la varianza di una differenza tra due serie di dati è uguale alla somma delle due varianze.

 

Anche nel caso di due campioni dipendenti, il calcolo della varianza attuato sulla colonna delle differenze risponde allo stesso principio: le variazioni d’errore (o residuo) presenti in ognuna delle due colonne dei dati possono essere nella stessa direzione, avere lo stesso segno rispetto alla media, e quindi annullarsi nella colonna delle differenze; possono altresì essere di segno opposto e quindi sommarsi.

 

Esempio 1.   Si vuole saggiare se la concentrazione algale influisce positivamente sulla crescita del Cladocero Daphnia magna. In laboratorio sono stati allevati 40 individui dello stesso ceppo: con attribuzione casuale, successivamente 20 individui sono stati posti in una soluzione con concentrazione algale di 120.000 cellule per ml e gli altri 20 in una soluzione con concentrazione algale di 24.000 celle per ml.

Dopo 20 giorni, è stata misurata la lunghezza (in mm) dei 20 individui di ognuno dei due gruppi e si sono ottenuti i valori riportati nella tabella sottostante:

 

 

 

 

Più dettagliatamente, si vuole sapere

1- se gli animali cresciuti nella soluzione con concentrazione algale maggiore (gruppo X₁)  hanno raggiunto dimensioni significativamente superiori a quelli cresciuti nella soluzione con concentrazione algale minore (gruppo X₂);

2- quale è il vero valore della differenza (d) nella crescita tra le due differenti situazioni di cibo

a)  alla probabilità a = 0.05

b)  alla probabilità a = 0.01

 

Risposta 1.   Saggiare se esistono differenze significative nelle dimensioni degli animali allevati nelle due differenti situazioni significa verificare l’ipotesi nulla

H₀: m₁ £ m₂

con ipotesi alternativa unilaterale

H₁: m₁ > m₂

 

Per ognuno dei due gruppi (X₁ e X₂), dai dati campionari si devono calcolare

-  il numero di osservazioni (n),

-  la media (),

-  la devianza  (SQ) e la varianza (S²)

 

 

Campione	X1	X2
	20	20
Media  ()	4,0443	3,04335
Devianza  (SQ)	0,30075	0,15326
Varianza  (S2)	0,015828	0,008066

 

 

Prima di procedere all’applicazione del test t, si deve controllare se le due varianze sono statisticamente uguali.

E’ possibile utilizzare il rapporto fra la varianza maggiore (che dal confronto risulta essere quella del gruppo X₁) e quella minore (del gruppo X₂):

 

F_(19,19)  =

 

Si confronta il risultato (1,962) con il valore critico di  per il livello del 5% (2,16); poiché il valore calcolato è minore di quello tabulato, si può assumere che le due varianze campionarie sono statisticamente uguali (anche se tale conclusioni potrebbe essere contestata, data la differenza ridotta con il valore critico prefissato).

E’ quindi corretto calcolare la varianza pooled

 mediante

 

e da essa ricavare  l'errore standard della differenza (es_d) fra le medie:

 

 

Il valore del t con 38 gdl è dato da

e risulta uguale a 28,96.

Si tratta di un test ad una coda perché interessa valutare se la maggior concentrazione algale produce anche una maggiore crescita delle Daphnie. Il valore critico del t di Student associato alla probabilità 1% con 38 gradi di libertà è 2,429, nettamente inferiore al 29,157 calcolato; si conclude quindi che la maggior concentrazione algale influisce in modo altamente significativo sulla maggior crescita delle Daphnie.

 

Risposta 2.

a - L'intervallo fiduciale alla probabilità a = 0.05 della differenza fra le due medie dato da

 

con i dati campionari diviene

(4,0443 - 3,04335) ± 1,686 ×0,034554

 

Da essa si calcolano i due limiti dell’intervallo

 

 

b - L'intervallo fiduciale alla probabilità a = 0.01 della differenza fra le due medie dato da

 

con i dati del campione è

 (4,0443 - 3,04335) ± 2,429 × 0,034554

 

I due limiti dell’intervallo (l₁ e l₂)

 risultano

l₁ = 0,917              l₂ = 1,086

 

Si può osservare come, sia alla probabilità a = 0.05 che a quella a = 0.01,

- l'intervallo fiduciale calcolato non comprenda lo 0, espresso come differenza attesa (d) nell’ipotesi nulla.

L'intervallo di confidenza mostra che la differenza reale (d) è positiva e significativa; di conseguenza, si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa espressa. Ovviamente con una probabilità pari a a che tale affermazione sia errata

 

ESEMPIO 2.  E’ stato misurato il valore del pH in due gruppi di laghi appenninici: 12 laghi hanno un bacino imbrifero ricco di rocce carbonatiche affioranti (X₁) e 13 laghi sono collocati in un bacino imbrifero senza rocce carbonatiche affioranti (X₂).

I valori misurati sono riportati nella tabella sottostante:

 

 

Si vuole conoscere:

1 - se la differenza media del pH dei 2 gruppi di laghi collocati in bacini imbriferi con diversa presenza di rocce carbonatiche è statisticamente significativa;

za media del pH tra le due situazioni

a)  alla probabilità a = 0.05

b)  alla probabilità a = 0.01.

 

Risposta  1.   In mancanza di conoscenze aprioristiche certe sul valore del pH nelle due differenti situazioni ambientali, il test è bilaterale; sono due campioni indipendenti e le ipotesi possono essere espresse mediante

H₀: m₁ = m₂               H₁: m₁ ¹ m₂

 

Dalle rilevazioni campionarie raccolte, si calcolano i dati necessari alla stima del valore del t per 2 campioni indipendenti

 

 

Prima di procedere all’applicazione del test si deve controllare se le due varianze possono essere considerate statisticamente simili, mediante il rapporto fra la varianza maggiore (che risulta essere quella appartenente al gruppo X₂) e quella minore (del gruppo X₁):

 

F _(12,11) =

 

Si confronta il risultato con il valore critico di F_(12,11) per il livello di probabilità 0.05 che è 2,79; poiché il valore calcolato (2,093) è minore di quello tabulato, le due varianze possono essere giudicate statisticamente uguali.

Di conseguenza, è possibile confrontare le due medie con il test t.

Dapprima si calcola la varianza pooled :  

 

 

 e da essa l'errore standard della differenza fra le due medie (es_d):

 

 

Applicando alla formula del test t per due campioni indipendenti

 

 

 i dati precedentemente calcolati, si stima il valore del t con 23 gdl

 

 che risulta uguale a 15,946.

Il valore critico del t di Student associato alla probabilità a = 0.01 con 23 gradi di libertà è 2,807 e risulta nettamente inferiore al valore calcolato (15,946).

I due gruppi di laghi hanno un pH medio statisticamente molto diverso.

 

Risposta 2.

a)  L'intervallo fiduciale della differenza fra le due medie associato alla probabilità a = 0.05 può essere calcolato mediante la formula:

 

Applicata ai dati dei due campioni a confronto, diventa

(8,117 - 7,136) ± 2,069 × 0,06152

 

 e permette di stimare i due limiti dell’intervallo

l₁ = 0,851              l₂ = 1,111

 

b)  L'intervallo fiduciale della differenza fra le due medie associato alla probabilità a = 0.01

 è:

(8,117 - 7,136) ± 2,807 × 0,06152

 e i limiti sono

l₁ = 0,804              l₂ = 1,158