METODI NON PARAMETRICI PER UN CAMPIONE

 

 

 

7.10.   TEORIA DEL TEST T DI WILCOXON  E  DELLA CORREZIONE PER I TIES.

 

 

E’ già stato chiarito che, se la condizione di simmetria è realizzata, per valutare la significatività della differenza (d) tra la mediana di una distribuzione sperimentale (me) e di quella attesa (me₀)

-          se l’ipotesi nulla H₀ è vera, la somma totale dei ranghi positivi (T⁺) e quella dei ranghi negativi (T^-) sono approssimativamente uguali,

-          se l’ipotesi nulla H₀ è falsa, una è maggiore dell’altra; in casi estremi, una è uguale a 0 (zero) e l’altra raggiunge il valore massimo, che dipende dal numero di dati (N).

In termini generali, tra le due somme dei ranghi (positivi = T⁺  e  negativi = T^-)

esiste la relazione

Ad esempio, con 7 dati (N = 7), se gli scarti dalla mediana attesa sono tutti positivi, si ha

-          T^- = 0

-          T⁺ = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28

Il secondo concetto importante è che, se l’ipotesi nulla H₀ è vera, con N dati il numero di possibili risposte è 2^N e quindi ognuna di esse ha una probabilità P = 1/2^N.

Applicato all’esempio significa che, poiché ognuno dei 7 ranghi può assumere valore positivo oppure negativo, si possono avere 128 (2⁷) risposte differenti e ognuna di esse, se indipendente come richiede la condizione di validità di questi test, ha una probabilità di realizzarsi P = 1/128.

 

Il testo di statistica non parametrica di P. Sprent pubblicato nel 1993 (Applied Nonparametric Statistical Methods, 2^nd ed., Chapman & Hall, London, 338 p.) spiega in modo semplice e dettagliato, con un esempio, come si associ ogni valore di T⁺ alla sua probabilità.

Sempre se l’ipotesi nulla è vera, con N = 7 si ha

-          T⁺ = 0  solo nel caso in cui tutte le differenze sono negative; la sua probabilità è P = 1/128;

-          T⁺ = 1  nel caso in cui solo la differenza di rango 1 è positiva; la sua probabilità è P = 1/128;

-          T⁺ = 2 nel caso in cui solo la differenza di rango 2 è positiva; la sua probabilità è P = 1/128;

-          T⁺ = 3 in due casi: quando è positiva solo la differenza di rango 3; quando sono positive contemporaneamente solo le differenze di rango 1 e 2; la sua probabilità totale è P = 2/128;

-          T⁺ = 4 in due casi: quando è positiva solo la differenza di rango 4; quando sono positive contemporaneamente solo le differenze di rango 1 e 3; la sua probabilità è P = 2/128;

-          T⁺ = 5 in tre casi: quando è positiva solo la differenza di rango 5; quando sono positive contemporaneamente solo le differenze di rango 1 e 4; quando sono positive solo le differenze di rango 2 e 3; la sua probabilità totale è P = 3/128;

-          T⁺ = 6 in quattro casi: solo rango 6; rango 1 e 5; rango 2 e 4; rango 3, 2 e 1; la sua probabilità totale è P = 4/128.

 

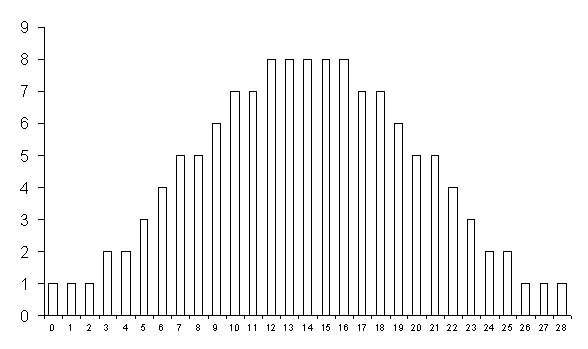
Nella tabella successiva sono riportati tutti i 28 possibili valori di T⁺ che è possibile ottenere con N uguale a  7 e la probabilità associata ad ognuno di essi.

 

 

 

 

La rappresentazione grafica evidenzia la simmetria della distribuzione.

 

Frequenze (in ordinata, su 128 casi possibili) dei valori di T (in ascissa, da 0 a 28) con N = 7

 

 

Tuttavia non appare normale, ma platicurtica. Inoltre i valori di probabilità si differenziano non in modo continuo ma con valori discreti, dato il basso numero di risposte possibili (128).

Per ottenere la normalità, almeno in modo approssimato, è necessario avere un numero (N) di osservazioni maggiore; secondo alcuni autori (come già accennato nei paragrafi precedenti) la distribuzione normale è già sufficientemente approssimata con N = 12.

 

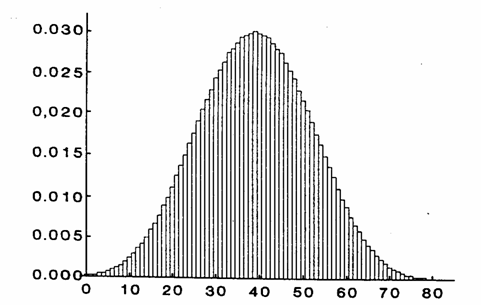
Con N = 12, il valore di T⁺ varia da 0 (zero ) a 78 (12 x 13 / 2) e il numero di possibili risultati sperimentali è 4096 (2¹²). La figura, che riporta (in ordinata) la probabilità associata ad ogni valore di T (in ascissa); appare molto simile alla normale.

Dalla distribuzione delle probabilità è semplice ricavare i valori critici di T⁺, quelli che delimitano la zona di rifiuto.

 

Se, sempre nell’esempio con N = 7, la regione critica scelta è a = 0.05,

-          in un test bilaterale permettono di rifiutare l’ipotesi nulla i valori di T⁺ uguali a 0, 1 e 2 in una coda e 26, 27 e 28 nell’altra coda; infatti la loro probabilità complessiva è P = 6/128 = 0,047;

-          in un test unilaterale permettono di rifiutare l’ipotesi nulla i valori di T⁺ uguali a 0, 1, 2 e 3 poiché la loro probabilità complessiva è P = 5/128 = 0.039; per T⁺ = 4 la probabilità complessiva diventa P = 7/128 = 0,0546 e pertanto supera il valore critico, non permettendo di rifiutare l’ipotesi nulla;

-          simmetricamente, se l’ipotesi unilaterale è nell’altra direzione, permettono di rifiutare l’ipotesi nulla valori di T⁺ uguali a 25, 26, 27 e 28; infatti la probabilità è P = 6/128 = 0,047;   T⁺ = 25 cade nella zona di non rifiuto, per lo stesso motivo di T⁺ = 4.

 

 

Distribuzione delle probabilità (in ordinata) associate ai valori T⁺ (in ascissa) con N = 12

 

 

 

Quando sono presenti dei valori identici (ties), si determina una alterazione nella distribuzione delle probabilità associate ai valore di T⁺.

A dimostrazione di questo concetto, si assuma un campione fortemente anomalo, rispetto alla condizione di continuità: un campione con N = 7 dati, che abbia prodotto le seguenti 7 differenze, di cui le 4 minori e le 3 maggiori tra loro uguali:

 

 

La trasformazione in ranghi diviene

 

 

Con questi 7 ranghi, calcolati sui loro valori medi, si ottengono i seguenti T⁺:

-          T⁺ = 0  solo nel caso in cui tutte le differenze sono negative; la sua probabilità è P = 1/128;

-          T⁺ = 2,5  quando uno solo dei 4 valori 2,5 è positivo; la sua probabilità è  P = 4/128;

-          T⁺ = 5 quando 2 dei 4 valori 2,5 sono positivi; tale evento può avvenire in 6 casi: quando sono positivi 1 e 2, oppure 1 e 3, oppure 1 e 4, oppure 2 e 3, oppure 2 e 4, oppure 3 e 4; la sua probabilità è  P = 6/128;

-          T⁺ = 6 in tre casi: quando uno solo dei 3 valori con rango medio 6 è positivo; la sua probabilità è P = 6/128.

 

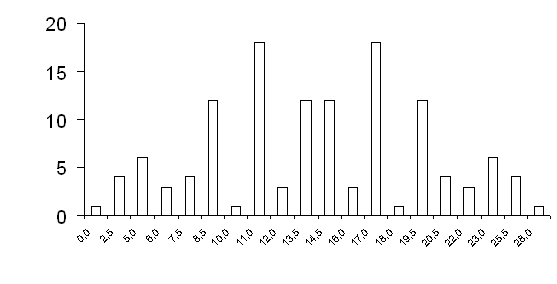
I valori possibili di T⁺ diventano 20 con le probabilità esatte riportate nella tabella sottostante

 

 

 

La rappresentazione grafica mostra le caratteristiche della distribuzione:

Frequenze (in ordinata, su 128 casi possibili) dei valori di T (in ascissa) con N = 7 e due ties.

 

Dal confronto con la precedente distribuzione per 7 dati, emerge che

1)       in ogni caso, anche con un numero eccezionalmente alto di ties come in questo esempio, la distribuzione è simmetrica,

2)       pure passando da una distribuzione unimodale a una distribuzione fortemente plurimodale,

3)       in cui le discontinuità sono molto più marcate;

4)       tuttavia, come sarà dimostrato successivamente, esse hanno pochi effetti sulla stima della probabilità;

5)       in conclusione, il metodo T è molto robusto.

 

Per chiarire questi concetti, cioè i ridotti effetti dei ties sulla potenza e sulla stima delle probabilità (robustezza) del test, è utile confrontare le probabilità associate ai valori di T nelle due diverse distribuzioni di dati.

In un test unilaterale,

-          nella distribuzione senza ties a T = 0  corrisponde una probabilità P = 1/128; nella distribuzione con i ties, la probabilità è identica;

-          nella distribuzione senza ties a T £ 1 corrisponde una probabilità P = 2/128; nella distribuzione con i ties, la probabilità è P = 1/128;

-          nella distribuzione senza ties a T £ 2 corrisponde una probabilità P = 3/128; nella distribuzione con i ties, la probabilità è P = 1/128;

-          nella distribuzione senza ties a T £ 3 corrisponde una probabilità  P = 5/128; nella distribuzione con i ties, la probabilità è identica;

-          nella distribuzione senza ties a T £ 4 corrisponde una probabilità  P = 7/128; nella distribuzione con i ties, la probabilità è  P = 5/128;

-          nella distribuzione senza ties a T £ 5 corrisponde una probabilità P = 10/128; nella distribuzione con i ties, la probabilità P = 11/128.

Esistono differenze nelle probabilità associate ai valori di T; ma esse sono piccole e concentrate solamente su alcuni valori. Soprattutto occorre tenere in considerazione che il caso utilizzato rappresenta una situazione estrema, per la quale tutti i testi affermano che non è corretto applicare il test T di Wilcoxon, ma che si deve ricorrere al test dei segni, proposto appunto quando si hanno molti valori identici o misurati in modo molto approssimato.