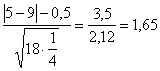METODI NON PARAMETRICI PER UN CAMPIONE

 

 

 

7.4.   TEST DEI SEGNI PER UN CAMPIONE

 

 

Il test dei segni (the sign test) per un campione è il test non parametrico più semplice per la verifica di ipotesi sulla tendenza centrale; è l’equivalente non parametrico del test t di Student per un campione.

Al posto dell’ipotesi nulla

H₀:

 contro l’ipotesi alternativa bilaterale

H₁: m ¹ m₀

 il test dei segni come misura di tendenza centrale utilizza la mediana, sia nella metodologia, sia nell’ipotesi nulla. Quindi

in test bilaterali verifica

H₀: me = me₀

 contro l’alternativa bilaterale

H₁: me ¹ me₀

 

Nel caso di test unilaterali,

 mentre nel test t di Student si verifica

H₀: m £ m₀    contro    H₁: m > m₀

oppure

H₀: m ³ m₀    contro    H₁: m > m₀

nel test dei segni si verifica

H₀: me £ me₀    contro    H₁: me > me₀

oppure

H₀: me ³ me₀    contro    H₁: me > me₀

(In alcuni testi, l’ipotesi nulla è sempre riportata come H₀ : me = me₀, anche nei test unilaterali).

 

La differenza fondamentale tra il test t e il test dei segni consiste nel fatto che il primo utilizza la distribuzione t di Student mentre il secondo si avvale della distribuzione binomiale, bene approssimata dalla distribuzione normale nel caso di grandi campioni.

Il test dei segni rappresenta una delle procedure più antiche nella statistica inferenziale. E’ stato utilizzato già nei primi anni del 1700 da Arbuthnot, per verificare se a Londra il rapporto fra maschi e femmine alla nascita superava il valore di 0,5. In tempi più recenti, ma sempre nelle fasi iniziali della statistica moderna, è stato riproposto da Sir R. A. Fisher nel suo testo Statistical methods for research workers del 1925. Da qui il nome, in alcuni testi, di Fisher’s sign test.

Nella ricerca sul campo ed in laboratorio, è frequente il caso in cui non tutti i dati hanno la stessa precisione o attendibilità. Nelle misure strumentali, quasi sempre si valutano correttamente quantità intorno alla media; ma sovente non si riesce a determinare valori troppo piccoli, che vengono indicati con minore di X, e/o valori molto grandi, fuori scala indicati con maggiore di Y. La serie dei dati riporta quantità intorno alla tendenza centrale, che possono essere ordinati ed altri agli estremi con molte sovrapposizioni.

Ad esempio, disponendo di un campione di N (12) osservazioni già ordinate in modo crescente,

 

<1     <1     1     2     4     5     8     9     10     12     19     >20

 

 può sorgere il problema di valutare se la mediana (me) sia significativamente minore di un valore di confronto, indicato nel caso in 15 (me₀).

E’ un test unilaterale, dove l’ipotesi nulla è

H₀:  me ³ me₀

e l’ipotesi alternativa è

H₁:  me < me₀

 

La procedura del test dei segni per un campione è semplice:

-          si confronta ogni punteggio con il valore di paragone (15), trasformando in segni negativi i punteggi inferiori ed in segni positivi quelli maggiori, ottenendo

 

-   -   -   -   -   -   -   -   -   -   +   +

 

- si contano i segni negativi (10) ed i segni positivi (2); la scala utilizzata dovrebbe essere continua e quindi non dovrebbero esistere valori uguali a quello di confronto, che danno una differenza di 0 da esso; qualora esistessero, le differenze uguali a 0 devono essere ignorate, con una pari riduzione delle dimensioni N del campione;

 

- se fosse vera l’ipotesi nulla, i segni negativi e quelli positivi dovrebbero essere approssimativamente uguali, con differenze imputabili alla casualità; si sceglie uno dei due valori, di solito quello minore (2): se è vera l’ipotesi nulla, dovrebbe non discostarsi troppo da N/2, corrispondente a 6 con i dati dell’esempio;

 

- con la distribuzione binomiale,

 

        nella quale   N = 12       r = 2       p = q = 1/2

        si stima la probabilità di trovare la distribuzione osservata e quelle più estreme nella stessa direzione (quindi per r che varia da 2 a 0); per evitare tanti calcoli si può ricorrere a tabelle che già forniscono le probabilità cumulate, per p = 1/2, con N e r che variano fino a 20 (riportata nella pagina successiva);

 

 

PROBABILITA’  CUMULATE  DELLA  DISTRIBUZIONE  BINOMIALE

 

 

 

 N = numero di osservazioni

 r = numero minore tra segni positivi e negativi

 

 

N

 

 

 

- applicando la distribuzione binomiale, si somma la probabilità relativa alla distribuzione osservata (r = 2) con quelle più estreme nella stessa direzione; se insieme determinano un valore inferiore alla probabilità a prefissata (di solito 0.05 quando si dispone di campioni piccoli), si può rifiutare l’ipotesi nulla in un test unilaterale.

 

Con i dati dell’esempio, N = 12   e   r = 2,

la tabella riporta una probabilità uguale a 0.019, corrispondente a 1,9% quando espressa in percentuale. Questo risultato significa che, se fosse vera l’ipotesi nulla, si ha una probabilità pari a 1,9% di trovare per caso una risposta uguale a quella trovata o ancor più estrema.

E’ una probabilità piccola, inferiore a 5%; di conseguenza, si rifiuta l’ipotesi nulla ed implicitamente si accetta quella alternativa, con la stessa probabilità di commettere un errore di I Tipo

 

- Per un test bilaterale, e quindi con ipotesi nulla

H₀:  me = me₀

 contro l’ipotesi alternativa

H₁:  me ¹ me₀

poiché la distribuzione binomiale è simmetrica quando p = 1/2 come atteso nell’ipotesi nulla, si deve moltiplicare la probabilità calcolata per 2: si rifiuta l’ipotesi nulla, quando questo ultimo valore è inferiore alla probabilità a prefissata.

Con i dati dell’esempio, l’ipotesi bilaterale ha una probabilità pari a 3,8% (1,9 x 2); di conseguenza anche in questo caso si rifiuta l’ipotesi nulla, ovviamente con una probabilità di errare pari a 3,8%.

 

Per N > 12 la distribuzione binomiale è già ritenuta sufficientemente grande per essere giudicata come approssimativamente normale; altri autori, più rigorosi, spostano questo limite a N >  20 osservazioni.

 

Per una distribuzione asintoticamente normale, si utilizza la distribuzione Z

Z =

in cui

-          X è il numero di segni positivi oppure negativi (di solito, in molti test viene consigliato di scegliere il numero minore, per motivi pratici, collegati alla tabella delle probabilità),

-          m è il numero atteso del segno prescelto ed è uguale a N/2 (con N = numero d’osservazioni),

-           s   è uguale a

 

Passando dalla distribuzione binomiale a quella normale, quindi da una misura discreta ad una continua, si deve apportare il termine di correzione per la continuità, come illustrato in vari esercizi d’applicazione della distribuzione normale.

 

ESEMPIO.  Da una serie di rilevazioni sulla quantità delle specie presenti in alcuni ambienti, sono stati derivati i seguenti 20 valori di biodiversità, già ordinati in modo crescente:

2,5  2,7  2,9  2,9  3,1  3,1  3,1  3,8  3,9  4,2  4,5  4,9  5,3  6,5  6,5  8,9  9,7  11,7  15,7   18,9

Si vuole valutare se la tendenza centrale di questa serie di rilevazioni è significativamente differente da 6,5 risultato il valore centrale dell’area in studi precedenti.

 

Risposta.

Per verificare l’ipotesi nulla

H₀: me = 6,5

con ipotesi alternativa bilaterale

H₁: me ¹ 6,5

con il test dei segni, si calcolano le 20 differenze.

Poiché 2 risultano uguali a 0, restano N = 18 osservazioni, delle quali solo 5 maggiori della mediana, per cui r = 5.

In un test unilaterale occorre calcolare le sei probabilità Pi

P_i =

con r che varia da 5 a 0.

La tabella delle probabilità cumulate in una distribuzione binomiale con p = q = 1/2, all’incrocio della colonna N = 18 e della riga r = 5 riporta 0,048.

Pertanto, in una serie di 18 misure, la probabilità di trovare per caso 5 valori positivi, o meno, è uguale a 4,8%. Poiché il test è bilaterale, si deve considerare anche la probabilità di avere 5 valori negativi.

In una distribuzione simmetrica come la binomiale con p = 1/2, la probabilità è uguale alla precedente; di conseguenza, si deve concludere che la probabilità di trovare scarti dall’atteso che siano uguali o superiori a quello trovato è uguale a 9,6%. Non è possibile rifiutare l’ipotesi nulla.

 

Per dimostrare come 18 osservazioni possano già essere considerate un grande campione ai fini pratici e per richiamare l’uso della distribuzione normale al posto della binomiale,

con i dati dell’esempio si stima

 

Z =

un valore di Z uguale a 1,65.

In una coda della distribuzione normale corrisponde ad una probabilità di circa 0,047. E’ quasi identica a quella fornita (0,048) dalla distribuzione binomiale cumulata.

 

In particolare quando si dispone di pochi dati, nella scelta del test più adatto insieme con il tipo di scala utilizzato e le caratteristiche della distribuzione dei dati assume importanza rilevante anche la potenza-efficienza dei test a confronto.

Come già ripetuto, l’ipotesi

H₀:  m = m₀

 

in campo parametrico è verificata mediante il test t di Student. Pertanto, l’efficienza asintotica relativa del test dei segni deve essere confrontata con il test t di Student.

 

Poiché la potenza-efficienza di un test dipende dalla forma di distribuzione dei dati, in vari testi di statistica, dei quali si riportano solo le conclusioni, i confronti sono fatti nelle condizioni che i dati abbiano

- una distribuzione normale,

- una distribuzione rettangolare,

- una distribuzione esponenziale doppia.

La potenza-efficienza relativa del test dei segni rispetto al test t di Student

-          con una  distribuzione normale dei dati è uguale a circa 0,64 (2/p),

-          con una distribuzione rettangolare dei dati è uguale a 0,33 (1/3),

-          con una distribuzione esponenziale doppia è uguale a 2.

 

Significa che, per avere la stessa probabilità di rifiutare l’ipotesi nulla, per ogni 100 dati ai quali sia stato applicato il test dei segni, il test t di Student richiede

-          64 dati nel caso di una distribuzione normale,

-          33 nel caso di una distribuzione rettangolare,

-          200 nel caso di una esponenziale doppia.

 

Quando i dati hanno una distribuzione fortemente asimmetrica, il test dei segni si fa preferire al test t di Student non solo per il rispetto delle condizioni di validità, ma anche perché è più potente.

Per la potenza a posteriori (b) e a priori (n) di questo test, fondato sulla distribuzione binomiale, si utilizzano le procedure illustrate nel capitolo IV per la proporzione con una binomiale.

E’ discussa anche nel capitolo successivo, nel test dei segni per due campioni dipendenti, che ha metodi identici a questo.