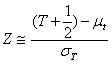METODI NON PARAMETRICI PER UN CAMPIONE

 

 

 

7.8.  Il test dei segnI PER RANGHI di Wilcoxon

 

 

Nel caso di una variabile continua, quindi

-  ordinabile in ranghi senza sovrapposizioni (anche se è accettato che pochi valori siano identici, eventualmente apportando una correzione chiamata correzione per i ties) e che

-  abbia una distribuzione simmetrica,

 l’ipotesi nulla sulla mediana

H₀: me = me₀

con ipotesi alternativa sia bilaterale che unilaterale può essere verificata anche ricorrendo al test proposto da  F. Wilcoxon nel 1945 (con l’articolo Individual comparison by ranking methods pubblicato su Biometrics Bulletin (diventato poi Biometrics) n. 1, pp. 80-83).

Utilizzando non solo il segno ma anche i ranghi, il test è più potente di quello dei segni come sarà quantificato alla fine del paragrafo; è quindi ad esso preferibile, quando i dati contengono tale livello ordinale d’informazione.

 

L’impostazione classica del test dei segni per ranghi di Wilcoxon (the Wilcoxon signed rank test), detto più semplicemente anche test T di Wilcoxon, nel caso di un campione permette di verificare se la tendenza centrale di una distribuzione si discosta in modo significativo da un qualsiasi valore prefissato di confronto.

 

Analogo al test t di Student per il confronto tra una media campionaria ed una media attesa, come termini di confronto utilizza la mediana e viene utilizzato quando

-  non è rispettata la condizione di normalità della distribuzione e/o

-  i dati raccolti sono stati misurati con l’attendibilità di una scala di rango.

 

La procedura del test dei segni di Wilcoxon per un campione può essere facilmente spiegata con l’applicazione ad un esempio.

Si supponga di voler verificare se un terreno abbia una quantità unitaria di sostanze azotate pari a 300 oppure significativamente minore, come lasciano supporre alcuni indicatori indipendenti da queste misure. A questo scopo, su un campione di 13 lotti (indicati con lettere da A ad O) con caratteristiche geologiche e di coltivazione molto differenti, è stata misurata la quantità unitaria di sostanze azotate.

 

Dalle analisi chimiche, si sono ottenuti i risultati () seguenti:

 

 

 

 

I dati confermano l’ipotesi espressa, cioè che la quantità reale media sia inferiore al valore di 300?

 

Risposta.   Si tratta di un test ad una coda, con ipotesi che utilizzano la mediana

H₀: me ³ 300       contro      H₁: me < 300

 

I motivi della scelta della mediana al posto della media sono diversi:

-          la mediana, come noto, è meno influenzata dai valori anomali;

-          se la distribuzione fosse normale, media e mediana coinciderebbero; quindi le inferenze sulla mediana possono essere estese alla media;

-          se la distribuzione dei dati mediante trasformazione diventa normale, il valore che identifica la nuova media coincide con quello della mediana precedente, ovviamente trasformato.

Nel caso specifico, l’asimmetria dei dati, come indicano i due valori molto più alti (430 e 440) e come sarebbe possibile quantificare esattamente attraverso il calcolo di g₁, non permette di utilizzare il test t di Student. E’ quindi necessario utilizzare un test non parametrico.

 

I passaggi logici fondamentali del metodo T di Wilcoxon sono:

1 - Calcolare le differenze d, con relativo segno, tra i dati raccolti () ed il valore () dell'ipotesi nulla (eliminando le eventuali differenze, non presenti in questo esempio, che risultassero uguali a zero):

 come riportato nella tabella sottostante

 

 

 

2 - Calcolare i ranghi () delle differenze (), considerate in valore assoluto (cioè ordinare gli N valori assoluti dal minore al maggiore; se esistono valori che hanno lo stesso rango, assegnare ad ognuno di essi un punteggio dato dalla media dei loro ranghi).

Dalla precedente distribuzione delle differenze, si ottiene la seguente serie di ranghi:

 

 

 

3 - Attribuire ad ogni rango il segno della differenza, già calcolata al punto 1; si ottiene la stessa serie di ranghi del punto 2, ma con il segno:

 

 

4 - Sommare i ranghi () dello stesso segno per calcolare T.

Ai fini del test, è indifferente scegliere il valore minore o maggiore tra somma dei ranghi positivi e la somma dei negativi. Abitualmente, si sceglie il valore ottenuto con il numero minore di dati, per il motivo semplice, ma spesso seguito nella prassi statistica, che richiede meno lavoro.

Con i dati dell’esempio, la scelta cade sulla somma dei ranghi con segno positivo (R+) appunto perché essi sono in numero minore. (Questi ranghi positivi sono già stati evidenziati in grassetto nella tabella precedente, per essere fatti risaltare maggiormente).

Da essi si ottiene

un valore di T uguale a 27.

 

 

5 - Stimare il valore medio, al quale dovrebbe tendere la somma dei ranghi T, nella condizione che l’ipotesi nulla H₀ sia vera: i ranghi positivi e quelli negativi dovrebbero essere casualmente distribuiti e dare quindi la stessa somma, in funzione del numero di dati.

La somma di N ranghi è

 

Quindi la media dei valori positivi o negativi m_T, che è la metà della somma di tutti i ranghi, dovrebbe essere

 

Calcolata sui 13 dati dell’esempio, la media (m_T) attesa nella condizione che l’ipotesi nulla sia vera, è

 m_T = 45,5.

 

6 - Se il valore espresso nell'ipotesi nulla (nell'esempio = 300) fosse la vera tendenza centrale della popolazione, la somma dei ranghi di segno positivo (T = 27) non dovrebbe essere significativamente differente dalla media dei ranghi ().

 

Nel caso di piccoli campioni (N £ 20), la significatività è fornita dalla tavola che riporta il valore critico inferiore (vedere la tabella sottostante e quella, più dettagliata, riportata nella pagina successiva).

 

 

Valori critici per il test dei ranghi con segno di Wilcoxon

per test unilaterali e bilaterali, alle probabilità a = 0.05   e   a = 0.01

(per campioni con N da 6 a 20)

 

 

Dove è riportato l’asterisco *  il campione è troppo piccolo, per un test significativo al livello di probabilità a stabilito.

 

 

Con i dati dell’esempio, per N = 13 nella colonna a = 0.05 per un test unilaterale il valore massimo di T è 21, al quale (nella tabella della pagina seguente) corrisponde una probabilità (calcolata in modo più preciso) a = 0.0471.

Il valore T calcolato (T = 27) con i dati dell’esempio è superiore a quello riportato nella tabella (21). Di conseguenza, nell’ipotesi che H₀ sia vera, la probabilità a di trovare un valore uguale o inferiore a 27 è superiore a 0.05.

Non si è in grado di rifiutare l'ipotesi nulla: la tendenza centrale dei dati raccolti non è significativamente minore di 300.

 

Se il test fosse stato bilaterale, quindi se la domanda fosse stata semplicemente se 300 poteva essere la tendenza centrale (la mediana) della distribuzione, i valori critici di confronto per il T (con N = 13) sarebbero stati

-          T = 17 per una probabilità a = 0.05

-          T =  9 per una probabilità a = 0.01.

 

 

Tavola dei valori critici di T nel test di Wilcoxon per un campione

e per due campioni dipendenti.

Le probabilità sono riferite ad un test unilaterale. Per un test bilaterale occorre moltiplicare per 2 il valore di a. Si può rifiutare l’ipotesi nulla alla probabilità a se il valore di T calcolato sui dati è minore o uguale a quello riportato in grassetto alla colonna corrispondente.

Per i valori critici di T intorno al valore a è riportata la probabilità esatta.

 

 

Nel caso di grandi campioni (N > 20), sempre nella condizione che H₀ sia vera, la somma dei ranghi dello stesso segno segue approssimativamente la distribuzione normale

 

 dove

-           è calcolata con la formula precedente

-           è la deviazione standard di T, determinata solamente da N

 secondo la relazione

 

Vari autori di testi di statistica applicata affermano che la formula di approssimazione per grandi campioni fornisce buoni risultati già quando N è maggiore di 10-12 osservazioni.

E' quindi possibile applicare le formule all'esercizio (con N = 13), per calcolare prima la deviazione standard

 

 e successivamente il valore di Z

 

Come è possibile verificare sulla tabella della distribuzione normale standardizzata, Z = 1,29 corrisponde ad una probabilità a uguale a 0.0985 (o 9,85%) in una coda della distribuzione.

Anche con questi calcoli, che permettono una stima più precisa della probabilità rispetto a quella abitualmente fornita dalla tavola sinottica dei valori critici, si deve concludere che i dati raccolti non permettono di rifiutare l’ipotesi nulla. Non  è possibile rifiutare l’affermazione che il valore 300 può essere la tendenza centrale della popolazione, dalla quale sono stati estratti i 13 valori campionari.

 

Il test dei segni per ranghi di Wilcoxon, come illustrato dalla metodologia, utilizza una quantità maggiore dell’informazione contenuta nei dati, rispetto al test dei segni.

Nei confronti del test dei segni, la sua efficienza relativa asintotica

-          con una  distribuzione normale dei dati è uguale a circa 1,50 (3/2);

-          con una distribuzione rettangolare dei dati è uguale a 3,00 (3/1);

-          con una distribuzione esponenziale doppia è uguale a 0,75 (3/4).

Significa che quando per un test con il T di Wilcoxon si hanno 100 dati, con il test dei segni ne servono

-          150 se la loro distribuzione è normale,

-          300 se la distribuzione è rettangolare ,

-          75 se la distribuzione è esponenziale doppia.

Il test T di Wilcoxon è più efficiente del test dei segni, eccetto quando la distribuzione dei dati è fortemente asimmetrica, come nel caso di una esponenziale doppia.

 

Per la scelta tra test parametrico e test non parametrico, è importante il confronto della potenza - efficienza tra

-          il test dei ranghi con segno T di Wilcoxon e

-          il test t di Student.

L’efficienza relativa asintotica del test T di Wilcoxon rispetto al test t di Student

-          con una  distribuzione normale dei dati è uguale a circa 0,95 (3/p),

-          con una distribuzione rettangolare dei dati è uguale a 1,

-          con una distribuzione esponenziale doppia è uguale a 1,50 (3/2).

Significa che il test T di Wilcoxon ha

-          un grado di efficienza molto vicina a quella del test t di Student (seppure leggermente inferiore e pari a 0,95), quando la distribuzione dei dati è approssimativamente normale;

-          una efficienza uguale (1), quando la distribuzione è rettangolare;

-          una efficienza sensibilmente maggiore (1,5), quando la distribuzione si allontana dalla normale.

Nella pratica della ricerca ambientale, in cui la distribuzione dei dati è spesso lontana dalla normalità, il test T di Wilcoxon è pertanto preferibile al test parametrico: assicura condizioni di validità più generali, senza perdere in potenza-efficienza (a volte aumentandola)

 

Inoltre, il test T di Wilcoxon, pur richiedendo la simmetria della distribuzione dei dati, è molto più robusto del test t di Student: fornisce risultati attendibili, anche quando i dati si allontanano sensibilmente dalle condizioni teoriche di validità.

 

 

ESEMPIO 1.   Con una serie di esperimenti è stato dimostrato che, in condizioni ottimali di temperatura, in 15 giorni una popolazione planctonica aumenta in media del 45 per cento.

Per valutare l’effetto inibente di una temperatura ambientale più bassa, sono stati misurati in natura i tassi di crescita di 10 campioni, composti necessariamente da un numero iniziale di individui molto variabile.

La tabella sottostante riporta il tasso di crescita (), in percentuale, di ogni campione:

 

 

Il loro tasso di crescita complessivo è significativamente minore del 45%?

 

Risposta.    Poiché i gruppi campionari sono di dimensioni nettamente diverse, i tassi di crescita misurati forniscono essenzialmente un’informazione di rango. Per confrontare tassi, rapporti o percentuali con test parametrici, è indispensabile che i dati siano riferiti a campioni di dimensioni simili. Infatti campioni con dimensione diversa hanno un’attendibilità diversa, come ha dimostrato l’intervallo fiduciale di una percentuale (vedi capitolo IV).

Inoltre, nel caso di percentuali o rapporti, a valori centrali differenti corrispondono varianze differenti. Di conseguenza, l’uso di test parametrici richiederebbe la trasformazione dei dati (nel caso specifico servirebbe la trasformazione in arcoseno, che sarà trattata ampiamente nel capitolo dedicato alle trasformazioni).

 

La domanda sulle percentuali di crescita richiede un test unilaterale; infatti, si vuole verificare se il valore centrale dei 10 dati sperimentali è inferiore al 45% stimato in condizioni ottimali.

Pertanto l’ipotesi nulla è

H₀: me ³ 45

e l’ipotesi alternativa unilaterale è

H₁: me < 45

 

Per rispondere a questo quesito, la procedura del test T di Wilcoxon prevede alcuni passaggi.

1 - Dapprima si calcolano le differenze () rispetto a 45:

 

 

 ottenendo 8 valori negativi e 2 positivi.

2 - Successivamente tali differenze devono

 essere trasformate in ranghi (), considerandone () il valore assoluto

 

 

 

3 – Ad ogni rango si attribuisce il segno della differenza già calcolata,

 ottenendo

 

 

 

4 -  Si sommano separatamente i ranghi () positivi e quelli negativi; in questo caso la somma con il minor numero di dati è quella dei ranghi positivi, il cui valore T è uguale a 3 (+1 e +2).

 

5 – Per la significatività, trattandosi di un campione piccolo, si ricorre alle tabelle dei valori critici.

Con N = 10, la tabella dei valori critici nella colonna con a =  0.05  fornisce la probabilità relativa a T = 10, che risulta uguale a 0.0420.

Il valore di T calcolato (uguale a 3) è nettamente minore di quello critico (uguale a 10) riportato nella tabella; di conseguenza, la probabilità che tale risultato sia casuale è inferiore a a = 0.05.

 

Una lettura più dettagliata della tabella può evidenziare che, per N = 10 e nella colonna della probabilità a = 0.01, a T = 5 corrisponde una probabilità esatta a = 0.0098. Il valore di T calcolato (uguale 3) è minore di quello tabulato (uguale a 5): la probabilità che il risultato ottenuto possa essere attribuito al caso è inferiore anche a 0.01.

In conclusione, si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa: con temperature più basse, i 10 campioni di plancton hanno avuto una crescita relativa la cui tendenza centrale è significativamente inferiore al tasso del 45%.

 

Secondo le indicazioni dei testi di statistica applicata, con 10 osservazioni il campione è troppo piccolo per usare correttamente la distribuzione normale. Tuttavia, per dimostrare la robustezza del metodo e per ricordare il procedimento di calcolo della probabilità ad essa associata, è utile il suo impiego anche ai dati di questo esempio.

Si inizia calcolando che, per   N = 10  e  T = 3 ,  nella condizione che l’ipotesi nulla sia vera

 la media attesa m_T

 è uguale a 27,5

 e la deviazione standard s_T con la formula

 

 risulta

 = 9,81

 uguale a 9,81.

Successivamente da essi, con la distribuzione normale

 si stima un valore di Z

 

 che uguale a 2,497 e che può essere arrotondato in 2,50.

Nella tabella della distribuzione normale, ad un valore di 2,50 in una coda corrisponde una probabilità  uguale a 0.00623 o 0,623%.

E’ una probabilità inferiore a 1%, come stimato mediante la tabella, nella prima parte dell’esempio.

 

In alcuni testi, con l’uso della normale quando il campione non è molto grande è suggerita la correzione per la continuità, per cui la formula

 

diventa

 

Anche in questo caso, per confrontare

-          la probabilità stimata utilizzando Z e

-          quella riportata nella tabella per piccoli campioni,

 si può calcolare Z  per T = 10

 

Con questi dati, il valore di Z risulta uguale a 1,78;  ad esso corrisponde una probabilità P = 0.0378.

Si può osservare che è un valore vicino, ma inferiore, a quello riportato nella tabella (per N = 10 e T = 10) che risulta uguale a 0.0420.

Tra i due valori è più corretto quello riportato dalla tabella. Quello ottenuto con Z è fondato sull’ipotesi che, anche con solamente 10 osservazioni, la distribuzione sia normale. In realtà l’allontanamento da questa condizione determina stime di probabilità inferiori al valore reale: quindi una conclusione non accettabile, perché permette di rifiutare l’ipotesi nulla più facilmente.

La correzione per la continuità

 

 fornisce un valore di Z = 1,73 e quindi una probabilità maggiore (0.0418) di quella precedente stimata con Z. La differenza con il valore di probabilità riportato nella tabella (0.420) è minima.

L’esempio dimostra l’utilità della correzione per la continuità.

 

In generale, quando nella stima della probabilità si commette un errore, la statistica accetta i risultati che forniscono probabilità superiori, non quelli che danno probabilità inferiori al valore reale, poiché con essi è più facile commettere un errore di Tipo II. Se si rifiuta l’ipotesi nulla con probabilità a < 0.05, la probabilità calcolata deve essere realmente minore di tale limite.