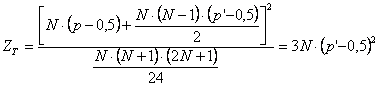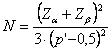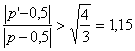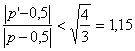8.5.  IL TEST T DI WILCOXON O test dei segni PER RANGHI, CON STIMA DELLA POTENZA.

 

 

Il test dei segni utilizza solo una parte minima delle informazioni contenute nei valori numerici. Ad esempio, non considera se i segni meno numerosi sono riferiti alle differenze maggiori o a quelle minori. Il test T (a volte indicato con W) di F. Wilcoxon per due campioni dipendenti (Wilcoxon paired-sample test) si giova anche dell’informazione relativa al rango ed attribuisce un peso maggiore alle differenze più grandi.

 

Principi e metodi sono identici a quelli del test di Wilcoxon della somma dei ranghi con segno, già applicati nel caso di un campione e derivati dall’articolo del 1945 (vedi Individual comparisons by ranking methods, pubblicato su Biometrics Bulletin (diventato poi semplicemente Biometrics) Vol. 1, pp. 80-83). Il metodo è stato successivamente divulgato nel 1964 dall’autore F. Wilcoxon e da R. A. Wilcox con il volume Some Rapid Approximate Statistical Procedures (edito da Lederle Laboratories, Pearl River, New York. 59 p.).

Il test compare ormai nelle librerie informatiche a maggiore diffusione, per l’uso ampio che ne è fatto nella statistica applicata, a causa della sua alta potenza (0.955 rispetto al test t quando la distribuzione dei dati è normale) e della generalità dei casi in cui può essere applicato. La presentazione della metodologia e le tavole dei valori critici per piccoli campioni sono riportati anche nel testo di statistica non parametrica  del 1975 di E. L. Lehmann (vedi Nonparametrics: Statistical Methods Based on Ranks, San Francisco, Holden Day).

 

Anche in questo caso, il test è più facilmente spiegato ricorrendo ad un'applicazione.

Si supponga di voler verificare se esistono differenze significative nei livelli mediani d’inquinamento tra due giorni (chiamati convenzionalmente X e Y), con caratteristiche meteorologiche nettamente differenti, tenendo in considerazione la variabilità presente tra ore.

A questo scopo, dalle ore 6 alle ore 20 e ogni 60 minuti, nella stessa zona di una città è stato rilevato il tasso di inquinamento atmosferico. I dati sono stati riportati nella tabella precedente (prime tre colonne):

 

 

 

Per rispondere al problema dopo aver definito che si tratta di

-          un test con ipotesi nulla

H₀ : d mediana = 0

-          e ipotesi alternativa bilaterale

H₁ : d mediana ¹ 0

 la metodologia richiede vari passaggi.

 

1 - Calcolare la colonna delle differenze con il loro segno:  (riportate in grassetto nella quarta colonna della tabella precedente).

 

2 - Eliminare dall’analisi le differenze nulle; la numerosità del campione sarà proporzionalmente ridotta (nell'esempio si elimina l’osservazione delle ore 18, poiché la differenza è uguale a 0; di conseguenza, il numero di osservazioni da 15, N diventa 14, come si rileva nella quinta colonna).

 

3 - Trasformare le differenze, considerate in valore assoluto, nel loro rango. Nel caso di due o più dati uguali, assegnare lo stesso valore, calcolato come media dei ranghi.

Nell'esempio sono presenti due differenze (X-Y) uguali in valore assoluto (+20 e -20), che occupano la 3^a e la 4^a posizione: per entrambe il rango è 3,5  dato da (3 + 4) / 2.

Vi sono altre tre differenze tra loro uguali (-30), che occupano la posizione 6^a, 7^a e 8^a: ad ognuna è assegnato rango 7, dato da (6 + 7 + 8) / 3.

Come dimostrato nel capitolo precedente, le misure ripetute (ties) hanno effetti trascurabili sul valore di T e quindi sulla stima della probabilità ad esso associata.

 

 

4 - Attribuire ad ogni rango il segno della differenza corrispondente (si ottengono i valori in grassetto della quinta colonna, sempre della tabella precedente).

 

5 - Sommare i ranghi con lo stesso segno. 

La somma dei ranghi positivi è

1 + 3,5 + 13 = 17,5

 

 mentre la somma dei ranghi negativi è

-3,5  –2  –7  -10  -12  –14  –5  –7 –7 – 9  -11 = 87,5

 

6 - Scegliere il totale minore: è il valore di T.

Nell'esempio, T è dato dai ranghi con segno positivo:

 

Per non commettere errori nei calcoli è utile ricordare, che la somma di N ranghi è uguale a

N (N+1)/2

 

Con i 14 dati dell’esempio (poiché una differenza è stata eliminata in quanto uguale a 0)

 la somma dei valori positivi (17,5) e di quelli negativi (78,5)

17,5 + 87,5 = 105

 deve essere uguale a

(14 x 15) / 2 = 105

 

7 - Secondo l'ipotesi nulla , la differenza tra le due serie di osservazioni appaiate dovrebbe essere uguale a zero. Di conseguenza, nella colonna delle differenze la somma dei ranghi con segno positivo e la somma dei ranghi con segno negativo dovrebbero essere uguali. Perciò il totale minore dovrebbe tendere ad un valore medio atteso m_T determinato da N, il numero di differenze o ranghi, secondo la relazione

 

Con i dati dell'esempio,

 il valore atteso della somma minore tra segni positivi e negativi dovrebbe tendere a 52,5.

 

8 - La significatività della differenza tra le due serie di dati appaiati è tradotta nella significatività della differenza tra T e _T; nell'esempio tra 17,5 e 52,5.

 

 

Per piccoli campioni (N £ 25), la significatività è fornita da tavole che riportano i valori critici di T in rapporto alla numerosità  del campione.

A questo scopo è possibile utilizzare una delle tabelle già presentate per un campione.

Altri testi riportano i valori critici in modo leggermente diverso, come nella pagina successiva che fornisce i valori massimi accettabili di T ai vari livelli di significatività, secondo la dimensione N del campione delle differenze.

 

La mediana della differenza è significativa alla probabilità a prescelta, quando il valore di T è uguale o inferiore a quello riportato nella tabella.

Per N = 14  e   = 0.05 in un test bidirezionale, il valore critico è 21.

Il valore di T (17,5) calcolato con i dati dell’esempio è minore. Si rifiuta l'ipotesi nulla e si accetta l'ipotesi alternativa.

Tra i due giorni esiste una differenza significativa nel valore mediano del tasso d’inquinamento.

 

Quando si programma un esperimento in cui utilizzare il test T di Wilcoxon è importante ricordare che per rifiutare l’ipotesi nulla alla probabilità a = 0.05,

-          in un test ad una coda, occorrono almeno 5 dati appaiati, la cui differenza sia sempre diversa da zero; si è in grado di rifiutare l’ipotesi nulla se le 5 differenze sono tutte dello stesso segno;

-          in un test a due code, servono almeno 6 coppie di dati, con differenze che siano tutte dello stesso segno.

 

Per test a una coda, per ottenere che la mediana delle differenze sia significativa

-          alla probabilità a = 0.01 servono almeno 7 coppie di dati,

-          alla probabilità a = 0.001 servono almeno 10 coppie, tutte dello stesso segno.

 

Valori critici per il test T di Wilcoxon con 2 campioni dipendenti

 

 

 

 

Per grandi campioni (N > 25), il valore della somma dei ranghi (T) è distribuito in modo approssimativamente normale: la significatività della differenza può essere saggiata con la distribuzione Z,

 usando la relazione

 

 dove la media attesa m_T è data da

 e la deviazione standard s_T è data da

 

L’applicazione del test T di Wilcoxon richiede che i campioni siano estratti da popolazioni con una distribuzione simmetrica, ma non necessariamente normale. Per il calcolo delle differenze tra dati appaiati, le osservazioni devono essere misurate in un scala d’intervalli.

La distribuzione normale, utilizzata per grandi campioni, fornisce una buona approssimazione già quando N è uguale 14-15 coppie di dati o differenze tra essi.

Nella tabella dei valori critici per piccoli campioni, per un test ad una coda è possibile osservare che, con N = 14, un valore di T = 25 risulta significativo alla probabilità a = 0.05.

Con la distribuzione normale, dove

m_T =  = 52,5

 e

 si ottiene un valore di Z

 uguale a -1,726.

In una coda della distribuzione ad esso corrisponde una probabilità a uguale a 0.0420, vicino al valore fornito dalla tabella. Si conferma in modo empirico come la normalità della distribuzione dei ranghi sia approssimativamente raggiunta anche con meno di 20 dati.

 

Quando i valori delle differenze sono distribuiti in un intervallo ristretto, si possono avere alcuni punteggi uguali o valutazioni ex-aequo (ties), in particolare in grandi campioni.

Come già presentato nel capitolo precedente per il caso di un campione, la media attesa _T non subisce variazioni; ma la varianza  diviene più ridotta, rispetto ai casi in cui ogni rango è attribuito con precisione.

A causa di queste valutazioni ex-aequo (ties) si impone una correzione di , che nel caso del test T di Wilcoxon consiste in una riduzione della varianza  pari a

dove

-          g è il numero di gruppi di ranghi identici,

-          t è il numero di dati con lo stesso rango entro ogni gruppo.

 

ESEMPIO 1.   I composti poco solubili in acqua e persistenti come alcuni pesticidi clorurati (il DDT e i PCB) si accumulano negli organismi acquatici e per loro tramite si trasferiscono lungo le catene alimentari. Anche nelle catene alimentari terrestri gli inquinanti si concentrano ai livelli trofici più elevati.

E’ stato catturato un gruppo di animali ed in essi è stata misurata la concentrazione di una sostanza tossica nel sangue. Dopo essere stati marcati sono stati liberati in un’area ritenuta inquinata.

A distanza di un mese, 13 sono stati ricatturati e per ognuno di essi è stata valutata nuovamente la presenza di sostanza tossica, rapportata ad un peso unitario (mg/Kg).

 

 

 

 

Si è realizzato un aumento significativo?

 

Risposta.  E’ un test ad una coda:

H₀ :  mediana 1^a  ³  mediana 2^a;           contro          H₁ :  mediana 1^a  <  mediana 2^a;

 

Seguendo i dati nella tabella riportata, la metodologia richiede alcuni passaggi:

1 - si calcolano le 13 differenze con il segno, tra tutte le coppie di misure;

2 - ad esse si attribuisce il rango relativo, considerando la differenza in valore assoluto ed ignorando la differenza nulla (dell’individuo F);

3 - ai 12 ranghi rimasti si attribuisce il segno della differenza;

4 - i valori negativi determinano la somma minore, con  T = 14;

5 - nella tabella per un test ad una coda alla probabilità a = 0.05 per N = 12, il valore critico di T riportato è 17;

6 - Il valore di T calcolato (14) è inferiore a quello tabulato (17) alla probabilità a prefissata (0.05).

Si rifiuta l’ipotesi nulla e quindi si accetta l’ipotesi alternativa: si è realizzato un aumento significativo nella concentrazione della sostanza tossica.

 

Rispetto al test t di Student per due campioni dipendenti, la potenza di questo test non parametrico ha valori identici a quella per un campione.

 

La stima della potenza del test di Wilcoxon per un campione è stata proposta da Gottfried E. Noether in un articolo del 1987 (vedi Sample Size Determination for Some Common Nonparametric Test, pubblicato su Journal of the American Statistical Association, Vol. 82, pp. 645-647). Nello stesso articolo ha proposto soluzioni anche per il test dei segni (già illustrato), il test U di Mann-Whitney per due campioni indipendenti, il test di correlazione t di Kendall. Il metodo proposto per un campione può essere applicato anche a due campioni dipendenti, come in questo caso, per valutare la significatività della mediana delle differenze rispetto a d.

Per determinare in modo approssimato la dimensione campionaria adeguata (N) ad ottenere un test significativo, con N sufficientemente grande da determinare che i valori di T siano distribuiti in modo approssimativamente normale, in accordo con la relazione

 

 

 dove il test T verifica se la quantità  p’-0,5  è maggiore o minore oppure diverso da zero:

 

 

Dall’ultima formula si ricava che N,

 che deve essere almeno uguale a

 dove

-           è il valore di Z alla probabilità a prefissata in un test che può essere sia bilaterale sia unilaterale,

-           è il valore di Z alla probabilità b prefissata in una distribuzione sempre unilaterale,

-          p’ deve essere sempre maggiore di 0,5.

Nelle formule precedenti compiono sia p sia p’.

Con p si indica la proporzione di valori positivi.

Con p’ si indica la proporzione di somme (X + X’) positive, dove X e X’ sono due osservazioni indipendenti. E’ una misura che deriva dalle medie di Walsh (Walsh averages), dato che somme e medie godono delle stesse proprietà.

 

ESEMPIO.  Determinare il numero minimo (N) approssimato di dati per un test bilaterale con a = 0.05 e un rischio b = 0.05  nel quale si vuole dimostrare significativa una differenza p’ = 0,9.

 

Risposta

Con  = 1,96  e  = 1,645 la dimensione (N) approssimata del campione

 è

 

 uguale a 27,08 che deve essere arrotondato a 28.

 

Anche nel test dei segni, illustrato nei paragrafi precedenti, al posto di p è possibile utilizzare p’.

Il valore di odds ratio è indicato con r’

 dove

 

Il valore associato di p’, per ritornare ad esso da r’,  è

 

Il rapporto tra p e p’ permette di valutare quando è conveniente utilizzare il test dei segni oppure quello di Wilcoxon, data la differente potenza dei due test in rapporto alle caratteristiche dei dati.

Secondo Noether,  il test di Wilcoxon

-          richiede meno osservazioni del test dei segni quando

 

 

-          richiede più osservazioni del test dei segni quando

 

 

L’efficienza relativa (relative efficiency), detta anche efficienza di Pitman (Pitman efficiency), del test dei segni il rapporto al test di Wilcoxon sia per un campione che per due campioni dipendneti è data dal rapporto

Efficienza relativa =

In particolare,

-          per la distribuzione uniforme essa risulta uguale a 1/3;

-          per la distribuzione normale essa risulta uguale a 2/3;

-          per la distribuzione logistica essa risulta uguale a 3/4;

-          per la distribuzione di Laplace e Cauchy essa risulta uguale a 4/3.