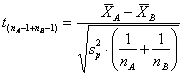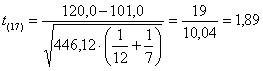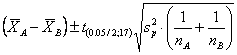METODI NON PARAMETRICI PER DUE CAMPIONI INDIPENDENTI

 

 

 

9.10. TEST S DI KENDALL E SUOI RAPPORTI CON IL TEST T E IL TEST U; POTENZA-EFFICIENZA DEI TRE TEST E CONFRONTI TRA I METODI.

 

 

Un altro test che affronta lo stesso problema, cioè il confronto tra le mediane di due campioni indipendenti, è il test S di Kendall. Fondamentalmente è una variazione del test U di Mann-Whitney, essendo fondato sulla stessa metodologia e esistendo una stretta corrispondenza tra i risultati. In mancanza dei valori critici di S, riportati in pochissimi manuali, con una trasformazione semplice è possibile utilizzare la tabella dei valori U. Tra i testi classici di statistica applicata che hanno una diffusione internazionale, questo test è riportato nel volume di Peter Armitage e Geoffry Berry del 1994 (Statistical Methods in Medical Research, edito da Blackwell Scientific Publication Limited, Oxford, tradotto in italiano nel 1996 con Statistica Medica. Metodi statistici per la ricerca in Medicina. McGraw-Hill, Libri Italia, Milano), dal quale sono tratti la presentazione, gli esempi e vari commenti.

 

Con un linguaggio molto sintetico, forse comprensibile solo a chi già conosce il test, questo volume presenta il test U di Mann-Whitney e il test sui ranghi di Wilcoxon; successivamente, in poche righe, espone il test S di Kendall, proposto appunto da M. G. Kendall nel suo volume del 1955 Rank Correlation Methods (2^nd ed., Charles Griffin and Co., London).

La presentazione di Armitage e Berry è utile soprattutto nella parte dove illustra le relazioni tra i metodi, poiché permette di passare con facilità dai risultati dell’uno a quelli dell’altro, come può essere richiesto nel confronto di pubblicazioni scientifiche appartenenti a scuole differenti.

Allo scopo di approfondire i concetti già presentati nei paragrafi precedenti e in particolare per esercitare lo studente a un linguaggio diverso da quello utilizzato in questo corso, con termini più rispondenti ai canoni classici del linguaggio statistico avanzato anche se spesso poco comprensibili ai meno esperti, si riporta quasi integralmente la trattazione di questi argomenti fatta nel testo. Per approfondimenti ulteriori si rinvia ad esso, consigliato a chi vuole avere a disposizione i testi fondamentali della statistica applicata alle discipline biologiche, mediche e ambientali.

 

Supponiamo di avere due gruppi di osservazioni: un campione casuale di  osservazioni, , proveniente dalla v. c. (variabile casuale) X e un campione casuale di  osservazioni, , proveniente dalla v. c. Y. L’ipotesi nulla da testare è che la distribuzione di  nella v. c. X è esattamente la stessa di Y. Vorremmo un test sensibile innanzitutto a spostamenti di localizzazione  delle distribuzioni, tali per cui le  tendono a essere più grandi (o più piccole) degli .

 

 

Nel test U di Mann-Whitney, le osservazioni sono poste in ordine crescente di grandezza. Vi sono  coppie (); di queste

U_XY è il numero di coppie per cui

U_YX è il numero di coppie per cui

Ogni coppia per la quale  conta 0,5 che è da aggiungere sia a U_XY che a U_YX.

Entrambe queste statistiche possono essere utilizzate come base per un test, con risultati esattamente equivalenti. Utilizzando U_YX, per esempio, la statistica deve essere compresa tra 0 e . In base all’ipotesi nulla, la sua attesa è

 

Valori elevati suggeriscono l’ipotesi di una differenza tra le popolazioni, con le  che tendono ad assumere valori maggiori delle . Reciprocamente, valori bassi di U_XY suggeriscono l’ipotesi che la distribuzione di X tenda a essere in posizione inferiore alla Y.

 

 

Nel test sui ranghi di Wilcoxon si presentano ancora una volta due statistiche equivalenti:

T₁ è la somma dei ranghi delle

T₂ è la somma dei ranghi delle

Valori bassi assumono ranghi bassi (cioè rango 1 è assegnato al valore più piccolo). A ogni gruppo di osservazioni uguali è assegnato il rango medio del gruppo.

 

Il valore minimo che la statistica T₁ può assumere si ha quando tutte le  sono più piccole di tutte le . In tal caso,

T₁ =

 

Il valore massimo per T₁ invece si ha quando tutte le  sono più grandi di tutte le .

In tal caso,

T₁ =

 

Il valore medio di T₁, cioè il valore atteso sulla base dell’ipotesi nulla,

 è

T₁ =

 

 

Il test S di Kendall è fondato su una statistica che è definita in funzione delle due statistiche di Mann-Whitney:

S = U_XY - U_YX

Il valore minimo (quando tutte le  sono inferiori a tutte le ) è

-

Il valore massimo (quando tutte le  sono superiori a tutte le ) è

+

 

Il valore medio o valore atteso in base all’ipotesi nulla è 0 (la media tra questi due).

 

 

Le relazioni tra i test sono semplici e possono essere derivate dalle formule precedenti, dato che tutte si rifanno alle dimensioni dei due campioni indipendenti.

Innanzitutto vi sono due relazioni tra le statistiche di Mann-Whitney (U_XY e U_YX) e tra le due statistiche di Wilcoxon (T₁ e T₂):

 

 

Esse dimostrano che i test basati sull’una o sull’altra statistica di ciascuna coppia sono equivalenti. Per esempio, dati T₁ e le dimensioni dei due campioni , si può immediatamente calcolare T₂ in base alla relazione  appena riportata.

 

In secondo luogo, i tre test (T, U, S) sono collegati dalle seguenti formule:

 

 

 

 

I tre test sono esattamente equivalenti. La probabilità di osservare un valore T₁ uguale o inferiore a quello osservato è esattamente uguale alla probabilità  che un valore U_XY sia maggiore o uguale a quello osservato. Pertanto, test di significatività basati su T₁ o su U_XY forniscono esattamente lo stesso livello di probabilità. La scelta tra questi due test dipende unicamente dalla familiarità con una certa forma di calcolo e dalla disponibilità delle tavole.

Con valori ripetuti nelle osservazioni, le formule della varianza vanno modificate.

Come per il test sui ranghi, le tavole dei valori critici sono da utilizzare con cautela in presenza di ripetizioni.

 

L’efficienza asintotica relativa del test T, del test U e del test S può essere valutata nei confronti del test t di Student per 2 campioni indipendenti, il test parametrico a loro equivalente. L’efficienza asintotica varia in funzione della distribuzione dei dati ed è uguale a quella già presentata per i test fondati sui ranghi nel caso di un campione e di 2 campioni dipendenti:

-          con una  distribuzione normale dei dati è uguale a circa 0,95 (3/p),

-          con una distribuzione rettangolare dei dati è uguale a 1,

-          con una distribuzione esponenziale doppia è uguale a 1,50 (3/2).

 

Come già ricordato in varie situazioni e sarà sviluppato in particolare nei paragrafi dedicati alle trasformazioni dei dati, le variazioni misurate in percentuale presentano problemi non trascurabili nell’analisi statistica parametrica:

-          le varianze di proporzioni medie differenti sono differenti, per cui occorre la trasformazione angolare;

-          quando le quantità iniziali sono molto diverse, la informazione reale è quella di rango;

-          i cambiamenti possono essere in aumento, per cui si ottengono valori molto alti che determinano una distribuzione asimmetrica;

-          ma possono anche essere in diminuzione, fino alla scomparsa totale del fattore analizzato; di conseguenza, il valore diventa –100 e può essere ripetuto varie volte, determinando una distribuzione fortemente bimodale, non riconducibile alla normale con nessuna trasformazione.

 

ESEMPIO 1.(Impostato sull’analisi di variazioni percentuali)

Illustriamo ora l’applicazione del test S di Kendall e dell’equivalente test U di Mann-Whitney ai seguenti due insiemi di dati:

 

X = Pazienti ospedalizzati,  = 32;  la notazione –100⁽¹²⁾ indica che i –100 sono 12

  -100⁽¹²⁾,  -93,  -92,  -91(2),  -90,  -85,  -83,  -81,  -80,  -78,  -46,  -40,  -34,  0,  +29,  +62,  +75,  +106,  +147,  +1321.

 

Y = Pazienti ambulatoriali,  = 32;  la notazione –100⁽⁵⁾ indica che i –100 sono 5

  -100⁽⁵⁾,  -93,  -89,  -80,  -78,  -75,  -74,  -72,  -71,  -66,  -59,  -41,  -30,  -29,  -26,  -20,  -15,  +20,  +25,  +37,  +55,  +68,  +73,  +75,  +145,  +146,  +220,  +1044.

 

Queste misure rappresentano la variazione percentuale dell’area di ulcere gastriche dopo 3 mesi di trattamento, eseguendo il confronto tra 32 pazienti ospedalizzati e 32 pazienti ambulatoriali.

 

Nel calcolo di S, quando vi siano valori ripetuti, non è necessario conteggiare 0,5 per ogni coppia () di valori uguali, perché quei contributi fanno parte sia di U_XY che di U_YX e pertanto si cancellano per la definizione di S. Pertanto si può calcolare S come P-Q, dove P e Q coincidono con U_XY e U_YX, quando si trascurino coppie di valori ().

In questo esempio si indichino con  i valori per pazienti ospedalizzati e con  quelli per pazienti curati in ambulatorio. Per calcolare P si consideri ogni osservazione del campione X e si conti il numero di pazienti del campione Y che risultano superiori a tale valore. Per alcuni primi valori di  si ottiene

 

 

Perciò

P = 12(27) + 5(26) + 3(25) + 24 + 23 + 17 + 2(16) + 11 + 9 + 7 + 2(4) + 2 + 0 = 662

Q = 5(20) + 19 + 15 + 11 + 7(10) + 9 + 5(7) + 2(6) + 2(5) + 2(4) + 3 + 2(2) + 2(1) = 298

 e

S = 662 – 298 = 364

Da

 dove

-           = dimensione campionaria delle

-           = dimensione campionaria delle

-          N =

-           = numero di valori ripetuti fra le osservazioni

 si ricava

 e infine

 

Utilizzando l’approssimazione normale, lo scarto normale standardizzato è

 

Z =  2,47    (P = 0.014)

 

 

Nella versione di Mann-Whitney, ogni ripetizione contribuisce per 0,5 a U_XY e a U_YX. Quindi per esempio

U_YX = 5(26) + 19,5 + 15 + 11,5 + … = 330

 

E(U_YX) =  = 512

 

(Nel testo qui riportato, E(U_YX) indica la media attesa di U nella condizione che H₀ sia vera; nei paragrafi precedenti, questa media attesa è sempre stata indicata con m_U)

Inoltre

U_YX – E(U_YX) = -182  (= )

 

  (= )    

 per cui

Z =  -2,47

 

 e  quindi lo scarto standardizzato è Z = -2,47, come in precedenza, a parte il segno.

E’ un esempio in cui la differenza tra i campioni di X e di Y non sarebbe stata rilevata da un test t. Le distribuzioni sono estremamente non – normali e il test t a due campioni dà

t = 0,51

 chiaramente non significativo.

 

 

Per la stima dell’intervallo di confidenza della differenza tra le due tendenze centrali, supponiamo che le due distribuzioni abbiano la stessa forma, ma differiscano di un d lungo la scala di misura, che risulta positivo quando le  tendono a superare le . Si può costruire l’intervallo di confidenza delle stime del parametro d  nel modo seguente.

In primo luogo, si noti che U_YX è il numero di coppie in cui . Pertanto, se si compongono tutte le  differenze di , allora U_YX è il numero di valori positivi (assumendo l’assenza di valori uguali). Di conseguenza, U_YX è una statistica del test per l’ipotesi che la differenza mediana sia pari a zero.

Sottraendo una quantità costante d da tutte le , e, quindi, da tutte le differenze, i due campioni risulterebbero effettivamente come estratti dalla stessa popolazione, verificando l’ipotesi nulla.

Calcolando nuovamente U_YX dopo la sottrazione, si otterrebbe un test per l’ipotesi che lo spostamento, o la differenza mediana, sia di fatto d.

I limiti di confidenza per lo spostamento d si ottengono, perciò, trovando quei valori che, sottratti da tutte le differenze, diano un risultato al limite della significatività.

Ordinando le differenze, l’intervallo di confidenza è la parte di mezzo della distribuzione, con un numero di differenze escluse  alle due estremità, in accordo con i valori critici del test U_YX. Il numero di valori da escludere può essere valutato utilizzando la tabella dei valori critici di U, come illustrato nel seguente esempio. Una stima puntuale del parametro d è data dalla mediana delle differenze, poiché si tratta del valore che, sottratto da tutte le differenze, renderebbe la statistica del test uguale al suo valore atteso.

 

ESEMPIO 2. (Confronto tra test e intervallo di confidenza parametrico e non parametrico)

Due gruppi di ratti femmine sono stati sottoposti a diete rispettivamente con alto (A) e basso (B) contenuto di proteine. Su ogni animale è stato calcolato l’aumento di peso il 28° e l’84° giorno di età. I risultati sono stati

 

 

 

Verificare la significatività della differenza tra le due diete e calcolarne l’intervallo confidenza con il test t e il test non parametrico corrispondente.

 

Risposta.

Per verificare l’ipotesi nulla

H₀: m_A = m_B      contro H₁: m_A ¹ m_B

 con il test t di Student

 si ottiene

 

 un valore di t = 1,89 con 17 g.d.l., al quale corrisponde una probabilità P = 0.076

Secondo i due autori, “la differenza non è significativa al livello del 5% e dà solo un’indicazione vaga dell’effetto delle diete”.

 

I limiti di confidenza della differenza calcolati con la formula

 

m_A – m_B =

 applicata ai dati dell’esempio

 risultano compresi tra –2,2  e  40,2.

 

Per verificare l’ipotesi

H₀: me_A = me_B      contro      H₁: me_A ¹ me_B

 con un test non parametrico,

 

-          è possibile utilizzare il test T di Wilcoxon

 

 

 

 con = 7,  = 12,  T₁ = 49,5  e  T₂ = 140,5

Poiché la tavola dei valori critici del T di Wilcoxon in un test bilaterale alla probabilità a = 0.05 riporta T₁ £ 46 la differenza tra le due mediane non risulta significativa.

 

Per calcolare l’intervallo di confidenza si utilizza distribuzione U, dove in un test bilaterale alla probabilità a = 0.05 è riportato il valore critico U £ 18.

Dopo aver calcolato tutte le 84 (12 x 7) possibili differenze

 

 

 

 

 per ottenere l’intervallo di confidenza al 95 % si eliminano le 18 più estreme in ogni coda.

Nella distribuzione ordinata delle differenze, si ricava che

-          il limite inferiore  è  –3,

-          il limite superiore  è  40,

-          mentre la mediana è 18,5 (cadendo tra 18, il 42° valore, e 19, il 43°).

 

Per campioni di dimensioni maggiori di quelli riportati nella tabella dei valori critici, cioè con  oppure  maggiori di 20, una buona approssimazione del numero di differenze da escludere in ogni estremità dell’insieme ordinato è dato dalla parte intera di

 

U =

Ad esempio,

-          per a = 0.05 bilaterale e con  =  = 20 il valore critico è U = 127;

 mentre con Z = 1,96 si stima

U =

U = 127,54

 

-          per a = 0.01 bilaterale e con  =  = 20 il valore critico è U = 105;

 mentre con Z = 2,576 si stima

 

U =

U = 104,77.