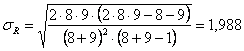METODI NON PARAMETRICI PER DUE CAMPIONI INDIPENDENTI

 

 

 

9.12.   Il  test  delle  successioni  per  due  campioni  INDIPENDENTI  o test  di  Wald-Wolfowitz

 

 

Il test della mediana, il test di Wilcoxon-Mann-Whitney, il test di Mann-Whitney per l'ordine robusto dei ranghi e il test di casualizzazione servono per verificare se tra due gruppi di osservazioni indipendenti esistono differenze significative nella tendenza centrale (nella mediana per i primi 3, nella media per l'ultimo). Sono test specifici per un solo parametro, come altri proposti per il confronto tra la variabilità di due gruppi, tra cui il test di Moses che verrà discusso successivamente.

Esistono anche test generalisti, come quello di Kolmogorov-Smirnov già presentato. Tra essi è da classificare il test delle successioni per 2 campioni indipendenti o test di Wald-Wolfowitz (Wald-Wolfowitz number of runs test).

Proposto da A. Wald e J. Wolfowitz nel 1940 (con l’articolo On a test whether two samples are from the same population sulla rivista Ann. of Math. Statist. n. 11 pp. 147-162), secondo alcuni autori di testi di statistica  trova le sue origini già in un lavoro di K. Pearson  del 1897 (The chances of death and other studies in evolution, London vol. I. cap. 2).

Il test di Wald-Wolfowitz è utile per verificare simultaneamente la significatività di qualunque differenza tra due distribuzioni campionarie, dovute ad effetti singoli o combinati dei 4 parametri di una distribuzione: la tendenza centrale, la dispersione, la simmetria e la curtosi.

 

Nel test delle successioni di Wald-Wolfowitz l'ipotesi nulla è che due serie campionarie di dati siano statisticamente uguali per tutti i parametri, in quanto estratte in modo casuale dalla stessa popolazione. L'ipotesi alternativa è che tra le due distribuzioni a confronto esista una differenza significativa in almeno un parametro, senza individuarne uno in modo specifico.

Il test è particolarmente utile quando si tratta di verificare l’ipotesi che due campioni possano appartenere ad alla stessa popolazione. In ecologia, nella ricerca ambientale e biotecnologica, è il caso di misure per qualsiasi variabile biologica o genetica tratta da animali o vegetali campionati in due diverse comunità o località: se appartengono alla stessa popolazione, con lo stesso patrimonio genetico, i due gruppi di animali o vegetali a confronto non dovrebbero differire per alcun parametro, né per la somma dei loro effetti; se invece fossero ormai da considerare due popolazioni differenti, quindi senza scambi genetici, dovrebbero differire nella media o nella varianza, nella simmetria o in quote significative e sistematiche di tali parametri. Lo stesso dicasi tra due serie di misure, appartenenti a due campioni indipendenti

 

Trattandosi di un test generalista, per valutare la significatività della differenza in un solo parametro tra due serie di osservazioni campionarie, la potenza del test delle successioni per 2 campioni indipendenti è minore di quella dei test specifici. Ma appunto perché considera anche fattori differenti da quelli analizzati da un test specifico, il confronto sulla potenza di un test generalista con un test specifico sul fattore considerato da quest’ultimo è ritenuto privo di senso da molti statistici.

 

Nonostante le differenze nell’ipotesi, la metodologia è uguale a quella del test delle successioni in un solo campione per eventi alternativi, quando l’ipotesi è unilaterale.

 

Come per i test precedenti, la metodologia ed i concetti di base possono essere presentati in modo semplice mediante un esempio.

 

Si supponga di voler verificare se esistono differenze significative nella distribuzione di due gruppi campionari (A e B riportati sotto) formati rispettivamente da 8 e da 9 osservazioni, per verificare se appartengono a due popolazioni differenti.

 

 

 

A differenza del test delle successioni per un solo campione, il test di Wald-Wolfowitz considera solo il caso di un numero di successioni inferiore all’atteso: se i due campioni a confronto appartengono a due popolazioni differenti, il numero di successioni tende ad essere minimo.

 

Le operazioni richieste dalla metodologia possono essere riassunte in alcuni passaggi fondamentali.

 

1 - Ordinare le due serie di dati campionari in ordine crescente, secondo il loro valore algebrico, conservando l'informazione del gruppo di appartenenza (nel test per un campione, le risposte di tipo binario erano ordinate secondo il tempo d’osservazione o rilevazione).

 

 

 

 

2 – Definire

-           la numerosità del campione con il numero maggiore di osservazioni,

-           la numerosità del campione con dimensione minore.

 

Contare il numero di osservazioni dei due gruppi e il numero di successioni (R)

 

 

 

 

Con i dati dell’esempio,

-          per il gruppo B,   = 9,

-          per il gruppo A,   = 9,

-          numero di successioni   R = 6.

 

E’ importante ricordare quale dovrebbe essere il numero di successioni, nel caso in cui le due distribuzioni differissero nella tendenza centrale, nella variabilità e/o nella forma (simmetria o curtosi) della distribuzione; in altri termini, se l’ipotesi nulla di appartenenza alla stessa popolazione fosse falsa.

 

Quando due gruppi hanno due valori significativamente differenti della tendenza centrale (H₀ falsa), nella sequenza ordinata dei dati i valori di un gruppo precedono quelli dell'altro gruppo. All'opposto, quando le due tendenze centrali sono uguali (H₀ vera) i dati dei due gruppi sono casualmente mescolati.

Nel primo caso, con H₀ falsa, il numero delle successioni è ridotto; nella situazione più estrema, quando la differenza tra le due tendenze centrali è rilevante, il numero di successioni tende ad essere solamente 2.

Nell’altro caso, quando H₀ è vera, il numero di successioni tende ad un valore medio, dipendente da  e .

 

Quando i due gruppi hanno una variabilità o dispersione differente (con tendenza centrale uguale), i dati del gruppo con maggiore variabilità tendono ad essere più frequenti dell’altro nelle due code della distribuzione. All'opposto, se i due gruppi avessero la stessa variabilità i dati dei gruppi sarebbero casualmente mescolati.

Nel primo caso con H₀ falsa, si hanno poche successioni; nel secondo caso con H₀ vera, il numero di successioni tende ad un valore medio, dipendente da  e .

 

Effetti simili provoca una differenza nella simmetria e nella curtosi: quando l’ipotesi nulla H₀ è falsa, si hanno poche successioni; quando l’ipotesi nulla H₀ è vera, il numero di successioni tende ad un valore medio, che dipende dal numero di osservazioni nei due gruppi.

3 - Nel caso in cui i due campioni appartengono alla stessa popolazione e quindi l'ipotesi nulla su tendenza centrale, variabilità, simmetria e curtosi è vera, il numero medio atteso di successioni m_R è uguale a

 

Con i dati dell'esempio:

 

il numero di successioni dovrebbe essere 9,47 (ovviamente arrotondato all’unità).

 

 

 

tavola  dei  valori  critici  nel  test  delle  successioni

PER DUE CAMPIONI INDIPENDENTI DI WALD-WOLFOWITZ

ALLA  PROBABILITA’  0.05

 

Le tabelle riportano i valori minimi significativi.

E’ significativo ogni numero R di successioni minore od uguale a quello riportato nella tabella.

Con n₁ si indica il campione maggiore, con n₂ il campione minore.

 

 

a = 0.05

 

 

	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
4			2
5		2	2	3
6		2	3	3	3
7		2	3	3	4	4
8	2	2	3	3	4	4	5
9	2	2	3	4	4	5	5	6
10	2	3	3	4	5	5	6	6	6
11	2	3	3	4	5	5	6	6	7	7
12	2	3	4	4	5	6	6	7	7	8	8
13	2	3	4	4	5	6	6	7	8	8	9	9
14	2	3	4	5	5	6	7	7	8	8	9	9	10
15	2	3	4	5	6	6	7	8	8	9	9	10	10	11
16	2	3	4	5	6	6	7	8	8	9	10	10	11	11	11
17	2	3	4	5	6	7	7	8	9	9	10	10	11	11	12	12
18	2	3	4	5	6	7	8	8	9	10	10	11	11	12	12	13	13
19	2	3	4	5	6	7	8	8	9	10	10	11	12	12	13	13	14	14
20	2	3	4	5	6	7	8	9	9	10	11	11	12	12	13	13	14	14	15

 

 

 

 

tavola  dei  valori  critici  nel  test  delle  successioni

PER DUE CAMPIONI INDIPENDENTI DI WALD-WOLFOWITZ

ALLA  PROBABILITA’  0.01

 

Le tabelle riportano i valori minimi significativi.

E’ significativo ogni numero R di successioni minore od uguale a quello riportato nella tabella.

Con n₁ si indica il campione maggiore, con n₂ il campione minore.

 

 

 

a = 0.01

 

 

	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
4
5				2
6			2	2	2
7			2	2	3	3
8			2	2	3	3	4
9		2	2	3	3	4	4	4
10		2	2	3	3	4	4	5	5
11		2	2	3	4	4	5	5	5	6
12		2	3	3	4	4	5	5	6	6	7
13		2	3	3	4	5	5	6	6	6	7	7
14		2	3	3	4	5	5	6	6	7	7	8	8
15		2	3	4	4	5	5	6	7	7	8	8	8	9
16		2	3	4	4	5	6	6	7	7	8	8	9	9	10
17		2	3	4	5	5	6	7	7	8	8	9	9	10	10	10
18		2	3	4	5	5	6	7	7	8	8	9	9	10	10	11	11
19	2	2	3	4	5	6	6	7	8	8	9	9	10	10	11	11	12	12
20	2	2	3	4	5	6	6	7	8	8	9	10	10	11	11	11	12	12	13

 

 

4 - L'ipotesi nulla H₀ viene verificata mediante la significatività della differenza tra il numero di successioni osservato R  ed il numero atteso m_R.

Nell’esempio, si deve verificare se R = 6 è significativamente diverso da m_R = 9,47.

 

Nel caso di piccoli campioni, si ricorre alla tabella dei valori critici, che forniscono il numero massimo di osservazioni nel caso di differenza significativa. Si utilizzano le stesse tabelle dei valori critici del test delle successioni per un campione, nel caso di ipotesi unilaterali. Quando il numero di successioni calcolato è più alto di quello riportato nella tabella, non si può rifiutare l’ipotesi nulla.

 

Con i dati dell'esempio, alla probabilità a = 0.05 il numero massimo riportato nella tabella per n₁ = 9 e n₂ = 8 (n₁ è il numero di osservazioni del campione maggiore) è 5, mentre il numero osservato con i dati sperimentali è 6.

Non si può rifiutare l'ipotesi nulla; non si è potuto dimostrare che le due distribuzioni di dati siano differenti per qualche caratteristica.

 

Nel caso di grandi campioni, R è distribuito in modo approssimativamente normale

con

dove m_R

e

 

Il campione dell’esempio è di piccole dimensioni; ma può essere utilizzato per mostrare la successione delle operazioni da eseguire nel caso di  grandi campioni .

Con i dati già riportati, dove R = 6  e  m_R = 9,47

 dopo aver calcolato s_R

 che risulta uguale a 1,988,

 si stima il valore di Z

 che risulta uguale a -1,74.

 

Nella tavola della distribuzione normale, in una coda della distribuzione al valore di 1,74 corrisponde una probabilità P = 0.0409 che permetterebbe di rifiutare l’ipotesi nulla alla probabilità a = 0.05.

Quando i dati dei due campioni a confronto sono pochi, con la distribuzione normale si sottostima la probabilità. E’ un errore che può essere corretto, quando il campione non è troppo piccolo.

 

Per un numero di osservazioni non grande, si deve apportare il termine di correzione per la continuità, che riduce il valore della differenza di 0,5 lasciando inalterata la varianza; abbassa quindi anche la significatività del test.

Il valore di Z diviene

 

Con i dati dell’esempio

Z  =    =    =  1,49

 

si ottiene Z = 1,49.

Ad esso, in una coda della distribuzione normale, corrisponde una probabilità uguale P = 0.0681; è un valore sufficientemente alto, che non permette di rifiutare l’ipotesi nulla alla probabilità a = 0.05.

La correzione per la continuità, da applicare nel caso di campioni non grandi, riduce la significatività della differenza tra successioni osservate ed attese; quindi abbassa la probabilità di rifiutare l’ipotesi nulla.

 

I ties, le osservazioni ex-aequo, non dovrebbero esistere nel test delle successioni per due campioni indipendenti; infatti, per applicare il test delle successioni, i punteggi dovrebbero essere misurati in una scala continua. La presenza di ties tra i due gruppi altera il conteggio delle successioni, ponendo situazioni di difficile soluzioni.

Il test delle successioni per due campioni indipendenti saggia l'ipotesi nulla H₀ di estrazione casuale dei due campioni indipendenti dalla stessa popolazione, contro ipotesi alternative multiple di differenze significative in almeno uno dei parametri delle due distribuzioni.

Il rifiuto dell'ipotesi nulla spesso richiede il ricorso ad altri test, per individuare la causa specifica o che ha fornito il contributo maggiore alla differenza riscontrata.

 

ESEMPIO.  Gli inquinanti organici ad effetto tossico formano una categoria estremamente ampia ed eterogenea; le molecole inquinanti o potenzialmente inquinanti sono centinaia di migliaia. Una classificazione elementare li suddivide in pesticidi, oli e idrocarburi; essa comprende anche la voce altri tossici organici, tra cui aromatici alogenati, aromatici volatili, diossine, cloroparaffine, clorofenoli, eteri difenilici alogenati, idrocarburi policiclici.

In due corpi idrici (A e B) è stata effettuata una serie di misure dell’inquinamento organico in condizioni simili.

 

 

Si vuole verificare se l’origine o causa dei valori riscontrati può essere comune.

 

Risposta.  Se l’ipotesi di una causa comune fosse vera, in termini statistici i parametri delle due distribuzioni campionarie non dovrebbero differire in modo significativo (H₀ vera).

Se la causa fosse diversa (H₀ falsa), con levata probabilità i due gruppi di dati dovrebbero differire per almeno un parametro della distribuzione.

Per applicare il test di Wald-Wolfowitz per due campioni indipendenti, si devono ordinare i due gruppi in una serie unica, mantenendo l’informazione del gruppo d’appartenenza.

 

 

Successivamente, si contano il numero di dati per campione ed il numero di successioni tra i due campioni a confronto

 

 

 Il numero di dati del campione maggiore è  = 11;

 il numero di dati del campione minore è  = 8;

 il numero di successioni tra i due campioni indipendenti è R = 6.

 

Sono due campioni di piccole dimensioni; per la stima della probabilità si deve ricorrere alla tabella dei valori critici.

Alla probabilità a = 0.05   per  = 11   e  = 8,  il valore critico riportato dalla tabella è 6.

Il valore di R calcolato è uguale a quello tabulato. Di conseguenza, alla probabilità P £ 0.05 si può rifiutare l’ipotesi nulla: le due serie di dati sono estratte da due popolazioni diverse.

Con probabilità uguale o inferiore a 0.05 di commettere un errore, si può sostenere che l’origine dell’inquinamento è differente.