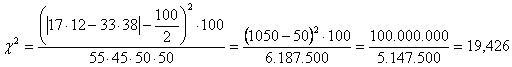METODI NON PARAMETRICI PER DUE CAMPIONI INDIPENDENTI

 

 

 

9.3.  TEST PER L’EFFETTO DELL’ORDINE DEL TRATTAMENTO O TEST DI GART

 

 

Quando si vogliono verificare gli effetti di due principi attivi somministrati in successione a due campioni indipendenti, le risposte degli individui ad ogni trattamento possono essere influenzate dall’ordine di somministrazione. I due gruppi di individui sono entrambi analizzati in due situazioni differenti, per cui l’esperimento a simile anche al test di McNemar per due campioni dipendenti.

Nella ricerca ambientale, può essere il gradimento espresso dai cittadini o il successo di due iniziative che in due località differenti sono state intraprese in ordine inverso. In una azienda, può essere il gradimento espresso dai clienti verso due campagne pubblicitarie attuate in ordine opposto.

 

Il test proposto da J. J. Gart nel 1969 (con l’articolo An exact test for comparing matched proportions in crossover designs, pubblicato su Biometrika vol. 56, pp.75-80) permette di verificare se esiste:

-  una differenza significativa tra la prima e la seconda somministrazione,

-  un effetto dovuto all’ordine.

 

Si utilizzano gli stessi test già presentati per le tabelle di contingenza 2 x 2, dove il confronto era tra il successo del principio attivo A e quello di B. Anche in queste due analisi, le ipotesi possono essere

-  solo bilaterali, se si ricorre al test c² e al test G,

-  bilaterali oppure unilaterali, con il metodo esatto di Fisher e con il test Z.

 

Per illustrare con semplicità la procedura, si supponga di somministrare due principi attivi (X e Y) a due campioni indipendenti (1 e 2). Allo scopo di valutarne gli effetti nelle due differenti settimane e quelli dovuti all’ordine,

-          ad un primo campione di 50 individui, nella prima settimana dell’esperimento è stato somministrato il principio attivo X e nella seconda settimana il principio attivo Y; dei 50 individui, 17 hanno mostrato miglioramenti più marcati durante la prima settimana con il farmaco X e 33 nella seconda settimana con l’uso del farmaco Y;

-          ad un secondo campione di 50 individui (di solito si formano campioni bilanciati per una maggior potenza del test, anche se non è strettamente necessario), nella prima settimana è stato somministrato il principio attivo Y e nella seconda il principio attivo X; in questo campione alla fine dell’esperimento, 12 hanno dato la loro preferenza a Y, preso nella prima settimana, e gli altri 38 al principio attivo X, preso nella seconda.

 

 

Per l’elaborazione statistica, questi dati devono essere impostati in una tabella di contingenza 2 x 2. Gli approcci sono differenti, sulla base di due diverse ipotesi nulle:

 

I – Per valutare se esiste una differenza significativa tra prima e seconda settimana, con ipotesi

H₀: La differenza nella percentuale di consenso tra la prima e la seconda settimana è nulla

H₁: La differenza nella percentuale di consenso tra la prima e la seconda settimana è significativa

 utilizzando la solita simbologia delle tabelle di contingenza 2 x 2, i dati devono essere presentati come nel modo seguente

 

 

 

Trattandosi di un test bilaterale e disponendo di un campione non grande, si stima

 

 

 un valore del c² con correzione che risulta uguale a 0,777 con 1 gdl.

Quindi non è significativo, corrispondendo ad una probabilità P superiore addirittura a  a = 0.25.

 

 

II – Per valutare se esiste una differenza significativa in rapporto all’ordine di somministrazione, con

H₀: L’ordine di somministrazione non ha effetti significativi;

H₁: L’ordine di somministrazione determina differenze significative

 i dati devono essere presentati come nella tabella

 

 

 

Trattandosi ancora di un test bilaterale e disponendo di un campione non grande, si stima

 

 

 un valore del c² con correzione che risulta uguale a 19,426 con 1 gdl.

E’ altamente significativo, poiché corrisponde ad una probabilità P inferiore a 0.001.

Infatti a = 0.001 ha un valore critico uguale a 10.828